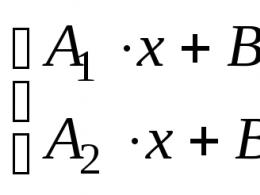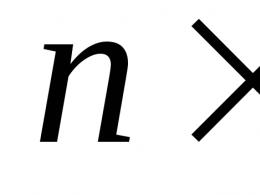Mianowany prez. Pomiędzy funkcjami: podstawowe zrozumienie i cel. b. Łączenie funkcji z podstawami

Wyrównanie funkcji według Heine (poprzez sekwencje) i Kosh (poprzez sąsiedztwo epsilon i delta). Nominacje są podawane w sposób uniwersalny, który jest stagnacją zarówno dla obustronnych, jak i jednostronnych między końcami i nieskończenie odległymi punktami. Jasne jest, że punkt a nie jest granicą funkcji. Dowód równoważności nominacji według Heiny i Cauchy.

Dyw. Również: Obrzeża punktu
Oznaczenie inter-funkcji w punkcie końcowym
Cel między funkcjami na niespójność

Pierwsze oznaczenie interfunkcji (dla Gein)

(x) w punkcie x 0 :
,
yakscho
1) to jest przebite obrzeże punktu x 0
2) ze względu na spójność (xn), co iść do x 0 :
, elementy leżące na obrzeżach,
dziedziczenie (f(xn)) zbiegają się do:
.

Tutaj x 0 mogę być jak liczby końcowe, więc mogę być nieskończenie odległymi punktami. Sąsiedztwo może być zarówno dwustronne, jak i jednostronne.

.

Inne przypisane funkcje (dla Kosh)

Liczba a nazywana jest granicą funkcji f (x) w punkcie x 0 :
,
yakscho
1) to jest przebite obrzeże punktu x 0 , funkcja de jest przypisana;
2) dla dowolnej liczby dodatniej ε > 0 również liczba δε > 0 , co kłamać w vіd ε , co kłamać dla wszystkich x , co leżeć przebite δ ε - wokół punktu x 0 :
,
wartość funkcji f (x) kłamać ε - wokół punktu a:
.

Krapki x 0 mogę być jak liczby końcowe, więc mogę być nieskończenie odległymi punktami. Sąsiedztwo może być zarówno dwustronne, jak i jednostronne.

Zapiszmy wizytę na pomoc symboli logicznych na podstawie tego przekleństwa:
.

W którym wszyscy wyznaczeni zastępcy znajdują się na obrzeżach równych odległości. Możesz podać równoważne oznaczenie, vicorist i całkiem blisko punktów.

Spotkanie z obrzeży vikoristannyam dovilnyh
Liczba a nazywana jest granicą funkcji f (x) w punkcie x 0 :
,
yakscho
1) to jest przebite obrzeże punktu x 0 , funkcja de jest przypisana;
2) dla dowolnego sąsiedztwa U (a) punkt a jest przebity wokół punktu x 0 , co dla wszystkich x , co należy przebić w pobliżu punktu x 0 :
,
wartość funkcji f (x) leżeć wokół U (a) punkty a:
.

Za pomocą symboli logicznych przyczynę tej niesławy można zapisać w następujący sposób:
.

Granice jednostronne i dwustronne

Wprowadźcie więcej określenia uniwersalności do faktu, że mogą zwyciężyć, czy to jakiegokolwiek rodzaju wokół. Jakbym jak zwycięski lew przebił obrzeża punktu końcowego, to usuwamy znak lewej granicy. Jakby wokół vikoristovuvaty wokół niewyraźnie odległego punktu, konieczne jest zaznaczenie granicy niespójności.

W celu ustalenia granicy dla Heina trzeba budować do punktu, w którym wystarczy, aby przejść do ostatniego miejsca, nakłada się dodatkową granicę - її elementy, które można winić za leżące w pobliżu punktu.

W celu wyznaczenia granicy według Kosha konieczna jest zmiana wyglądu granicy w skórze, aw nerwowości zastępczy wygląd obrzeży punktu.
Dyw. „Kropka Navko”.

Wyznaczony, że punkt a nie jest granicą funkcji

Często winą jest konieczność pokonania umysłu, że punkt a nie jest granicą funkcji w . Zatrzymajmy to do końca tygodnia, chwaliłem się bardziej. smród, przyznajemy, że funkcja f (x) zaznaczone na deakim przebite wokół punktu x 0 . Punkty a i x 0 mogą być jak ostatnie liczby, tak nieubłaganie odległe. Wszystkie sformułowane poniżej powinny być zarówno dwustronne, jak i jednostronne pomiędzy.

Według Heinego.
Numer a nie funkcja f (x) w punkcie x 0 : ,
yakscho to taka sekwencja (xn), co iść do x 0 :
,
elementy, które leżą wokół,
jaka sekwencja? (f(xn)) nie zbiegaj do:
.
.

By Kosh.
Numer a nie funkcja f (x) w punkcie x 0 :
,
yakscho to taka dodatnia wielkość ε > 0 więc dla dowolnej liczby dodatniej δ > 0 іsnuє tak x , co należy przebić δ - wokół punktu x 0 :
,
jaka jest wartość funkcji f (x) nie kłam ε - wokół punktu a:
.
.

Zrozum, że punkt a nie jest granicą funkcji w , to ce nie oznacza, że ​​nie może być granicą. Ewentualnie, іsnuє granica, ale nie zrobię. Jest to również możliwe, jeśli funkcja jest przypisana do przebicia wokół punktu , ale nie do granicy w .

Funkcjonować f(x) = grzech(1/x) brak limitu dla x → 0.

Na przykład funkcja jest przypisana w , ale nie pomiędzy. Jako dowód bierzemy sekwencję. Wygrane zbiegają się do punktu 0 : . W takim razie odłamki.
Weź sekwencję. Vaughn również zbiegają się do punktu 0 : . W takim razie odłamki piwa.
Ta sama granica nie może równać się tej samej liczbie a. Skutecznie, z Іsnuє sledovnіst, Z yakoї. Dlatego, niech będzie tak, jakbyś widział zero, liczba nie jest granicą. Ale to też nie jest granica, odłamki są sekwencją, do tego.

Równoważność nominacji między według Heine i Cauchy

Twierdzenie
Oznaczenie funkcji interfunkcyjnych według ekwiwalentu Heiny'ego i Cauchy'ego.

dowód

Podczas udowadniania zakłada się, że funkcja jest przypisana do deyakіy przebitego w pobliżu punktu (kіntsevoy lub niewyraźnie daleko). Punkt a może być również skończoną liczbą niewyraźnie odległych.

Dowód Heinego ⇒ Cauchy

Niech funkcja będzie w punkcie między zgіdno z pierwszymi spotkaniami (za Gein). Tak więc, aby była sekwencją, co powinno być przebite wokół punktu, a może być pomiędzy
(1) ,
między sekwencjami dorivnyu a:
(2) .

Zostanie wykazane, że funkcja może znajdować się pomiędzy w punkcie Koshy. Tobto do stosowania na skórę, scho dla wszystkich.

Nie akceptujmy. Pozwólcie, że umyję (1) ten (2) vikonan, ale funkcja nie może przekraczać granic Kosh. Tobto іsnuє tak, scho dla be-kto іsnuє, więc scho
.

Załóżmy, że de n jest liczbą naturalną. Co więcej, Todi іsnuє
.
W ten sposób nakłanialiśmy do przejścia do sekwencji, ale między sekwencjami nie jest dobre a. Twierdzenia o superechitach o umyśle.

Pierwsza część jest zakończona.

Cauchy'ego ⇒ dowód Heinego

Niech funkcja będzie w punkcie między zgidnem a innymi wyznaczeniami (dla Koshoy). Tobto dla być kim іsnuє, scho
(3) dla wszystkich.

Zostanie wykazane, że funkcja może znajdować się między a a punktem poza Heinem.
Weźmy dobrą liczbę. Zgіdno z vznachennyam Koshi іsnuє number, więc vykonuєtsya (3).

Vіzmemo dovіlnu posіdovnіst, scho leżą przebite obrzeża i idą do. Dla wyznaczonej sekwencji, co iść, cokolwiek to jest, co
w .
Todi z (3)
w .
W takim razie Oskіlki tse vykonuєtsya dla kogoś
.

Twierdzenie zostało zakończone.

Literatura wikoristanu:
L.D. Kudryavtsi. Przebieg analizy matematycznej. Tom 1. Moskwa, 2003.

W tych statystykach możemy powiedzieć, co znajduje się między funkcjami. Tył głowy można wytłumaczyć istotnymi momentami, które są jeszcze ważniejsze dla zrozumienia istoty tego zjawiska.

Zrozumienie granic

W matematyce fundamentalnie ważne jest zrozumienie niespójności, ponieważ jest ona oznaczona symbolem ∞. Yogo slіd razumіti jak nieskończenie duża + ∞ lub nieskończenie mała - ∞ liczba. Jeśli mówimy o niespójności, często możemy być na vіdrazu vіrazu vіdva tsі її sensi, prote record + ∞ lub - ∞ nie varto po prostu zastąp go ∞.

Wpis między funkcjami może wyglądać jak lim x x 0 f (x) . Główny argument x piszemy w dolnej części, a po dodatkowej strzałce można wskazać, jaka wartość x 0 zostanie użyta. Ponieważ wartość x 0 jest określoną liczbą rzeczywistą, możemy użyć prawej granicy funkcji w kropkach. Jeśli wartość x 0 nie jest niespójnością (nieważne, ∞ , + ∞ lub - ∞), to powinniśmy mówić o granicy funkcji na niespójność.

Między buvaє kіntsevoi a neskіchennoi. Yakshto vіn dorivnyuє konkretna fikcyjna liczba, tobto. lim x → x 0 f (x) = A , wtedy nazywa się to granicą końcową, ponieważ lim x → x 0 f (x) = ∞ , lim x → x 0 f (x) = + ∞ lub lim x → x 0 f (x) = - ∞

Chociaż nie możemy określić ani kіntseve, ani niewybaczalnego znaczenia, oznacza to, że nie ma czegoś takiego. Tyłek tej vipadki może znajdować się między zatokami na niespójności.

W tym miejscu wyjaśnimy, jak poznać znaczenie inter-funkcji w punkcie niespójności. Dla kogo musimy zrobić główny cel i wróżenie, jakie są ciągi liczbowe, a także ich opłacalność i różnorodność.

Spotkanie 1

Liczba A jest granicą funkcji f(x) jako x → ∞, więc ciąg jej wartości będzie podobny do A dla każdego nieskończenie dużego ciągu argumentów (ujemnego lub dodatniego).

Wpis między funkcjami może wyglądać tak: lim x → ∞ f (x) = A .

Spotkanie 2

Gdy x → ∞ między funkcją f (x) jest niewyczerpalny, więc ciąg ma znaczenie dla tego, czy istnieje nieskończenie wielki ciąg argumentów, będzie on również nieskończenie wielki (dodatni lub ujemny).

Notacja wygląda tak: lim x → f (x) = ∞ .

tyłek 1

Przynieś równość lim x → ∞ 1 x 2 = 0 za pomocą głównej wartości między x → ∞ .

Rozwiązanie

Nauczmy się z ciągu wartości funkcji 1 x 2 dla nieskończenie dużego dodatniego ciągu wartości argumentu x = 1, 2, 3,. . . , n, . . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 n 2 > . . .

Mi bachimo, że wartości zmieniają się krok po kroku, krok do 0. na zdjęciu:

x = - 1, - 2, - 3,. . . , - n , . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . >1-n2>. . .

Tutaj możesz również zobaczyć monotonny upadek nano, co potwierdza słuszność tego dla umysłu gorliwości:

Sugestia: Vіrnist tsgogo za przyniesioną gorliwość umysłu.

tyłek 2

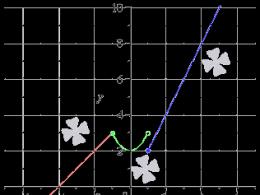
Oblicz między lim x → ∞ e 1 10 x .

Rozwiązanie

Nie bez powodu, jak poprzednio, z zapisu ciągów wartość f(x) = e 1 10 x dla nieskończenie dużego dodatniego ciągu argumentów. Na przykład x = 1, 4, 9, 16, 25. . . , 10 2 , . . . → +∞.

e 1 10; e 4 10; e 9 10; e 16 10; e 25 10; . . . ; e 100 10; . . . == 1, 10; 1, 49; 2, 45; 4,95; 12, 18; . . . ; 22026, 46; . . .

Bachimo, że dana sekwencja jest nieskończenie dodatnia, również f(x) = lim x → + ∞ e 1 10 x = + ∞

Przekazujemy do rekordu wartość nieskończenie dużego ciągu ujemnego, na przykład x = - 1, - 4, - 9, - 16, - 25,. . . , - 10 2 ,. . . → -∞.

e-110; e-4 10; e-9 10; e-16 10 ; e-25 ​​10 ; . . . ; e-100 10 ; . . . == 0,90; 0,67; 0,40; 0,20; 0,08; . . . ; 0,000045; . . . x = 1, 4, 9, 16, 25. . . , 10 2 , . . . →∞

Jeśli nie ma śladów zera, to f (x) = lim x → ∞ 1 e 10 x = 0 .

Najpierw rozwiązanie problemu pokazano na ilustracji. Niebieskie kropki oznaczają ciąg wartości dodatnich, zielone kropki ciąg wartości ujemnych.

Sugestia: lim x → ∞ e 1 10 x = + ∞ , pr і x → + ∞ 0 , pr і x → - ∞ .

Przejdźmy do metody obliczania funkcji międzyfunkcyjnych w punktach. Dla kogo musimy wiedzieć, jak poprawnie wyznaczyć granicę jednostronną. Pomóż nam poznać pionową asymptotykę wykresu funkcji.

Spotkanie 3

Liczba B є granica funkcji f(x) jest zaostrzona jako x → a, więc jeśli ciąg wartości її schodzi w dół do podanej liczby, jeśli w funkcji x n występuje jakikolwiek ciąg argumentów, to zejdź w dół do< a).

Taka granica na arkuszu jest oznaczona jako lim x → a - 0 f (x) \u003d B.

Teraz możemy sformułować, co znajduje się między funkcjami osoby praworęcznej.

Spotkanie 4

Liczba B є granica funkcji f(x) jest prawoskrętna jako x → a, więc jeśli ciąg wartości її schodzi w dół do podanej liczby, jeśli w funkcji xn występuje jakikolwiek ciąg argumentów, to zejdź do a) .

Qiu pomiędzy zapisuje się jako lim x → a + 0 f (x) = B .

Możemy przypisać między funkcjami f (x) w tym samym punkcie, jeśli konieczne jest ustalenie równych granic między lewą i prawą stroną, wtedy. lim x → f(x) = lim x → a - 0 f(x) = lim x → a + 0 f(x) = B . W czasach niespójności obie funkcje międzyfazowe w punktach zewnętrznych również będą niedokładne.

Teraz możemy zrozumieć umówione spotkanie, po spisaniu decyzji o konkretnym zadaniu.

tyłek 3

Przynieś, jaka jest ostatnia granica funkcji f (x) = 1 6 (x - 8) 2 - 8 przy x 0 = 2 i oblicz jej wartość.

Rozwiązanie

Aby rozwiązać problem, musimy odgadnąć znaczenie interfunkcji w danym punkcie. Możemy ci powiedzieć, scho s vihіdnoї ї ї є mezha zlіva. Zapisujemy sekwencję wartości funkcji, tak aby była zbieżna do x 0 = 2 x n< 2:

f(-2); f(0); f(1); f 1 1 2; f 1 3 4; f 1 7 8; f 1 15 16; . . . ; f 1 1023 1024; . . . == 8, 667; 2667; 0,167; - 0,958; - 1489; - 1747; - 1874; . . . ; - 1998; . . . → - 2

Sekwencja wywołana przez Oskіlki do zbudowania do -2 możemy zapisać, że lim x → 2 - 0 1 6 x - 8 2 - 8 = - 2 .

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Wartość funkcji tej sekwencji wygląda tak:

f(6); f(4); f(3); f 2 1 2; f 2 3 4; f 2 7 8; f 2 15 16; . . . ; f2 1023 1024; . . . == - 7, 333; - 5, 333; - 3 833; - 2958; - 2489; - 2, 247; - 2, 124; . . . , - 2001,. . . → - 2

Ta sekwencja również jest zbieżna do -2 , a następnie lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2 .

Odjęliśmy, że między prawą i lewą stroną funkcji będą równe, a następnie między funkcjami f(x) = 1 6 (x - 8) 2 - 8 w punkcie x 0 = 2 існує, і lim x → 2 1 6 (x - 8) 2 - 8 \u003d - 2.

Rozwiązanie widać na ilustracji (zielone kropki - ciąg wartości, które zbiegają się do x n< 2 , синие – к x n > 2).

Sugestia: Pomiędzy prawą i lewą stroną funkcji będą równe, więc pomiędzy funkcjami jest prawda, a lim x → 2 1 6 (x - 8) 2 - 8 = - 2.

Aby lepiej zrozumieć teorię pomiędzy, w trosce o siebie, przeczytaj artykuł o ciągłości funkcji w punkcie i głównym punkcie widzenia.

Jak zapamiętałeś ułaskawienie w tekście, bądź miły, zobacz to i naciśnij Ctrl + Enter

Między funkcjami-Numer a będzie granica aktualnej wartości, która się zmienia, gdyż w procesie jej zmiany wartość zmiany nie będzie zbliżona do a.

Innymi słowy, liczba Aє funkcja graniczna y = f(x) w punkcie x0, co do tego, czy istnieje ciąg punktów z obszaru funkcji przypisanej, nierówny x0 i zbiegają się do punktu x 0 (lim x n = x0), sekwencja drugich wartości funkcji zbiega się do A.

Wykres funkcji, między tymi z argumentami, co nie jest niezgodnością, dobrze L:

Wartość ALEє granica (wartości brzegowe) funkcji f(x) w punkcie x0 na vipadku, czy istnieje ciąg punktów , jak zbiegają się w górę x0, ale jaka się nie mścij x0 jak jeden z własnych elementów (tobto na przebitych obrzeżach x0), ciąg wartości funkcji zbiegają się do A.

Między funkcjami według Cauchy'ego.

Wartość A będzie funkcja graniczna f(x) w punkcie x0 u vipadku, jak w przypadku skin forward wzięto liczbę ujemną ε będzie ci znana nieznana liczba δ = δ(ε) więc co za argument ze skórą x to zadowala umysł 0 < | x - x0 | < δ , bude vykonano nerіvnіst | f(x) A |< ε .

Będzie prostsze, dzięki czemu zrozumiesz istotę między-rzeczowych podstawowych zasad wiedzy jogi. Te między funkcjami f(x) w x co pragne? a dorivnyuє A, należy napisać w następującej kolejności:

Co więcej, znaczenie, które pragne się zmieniło x, może nie tylko liczba, ale też niespójność (∞), czasem +∞ lub -∞, inaczej nie możesz być między nimi.

Aby zrozumieć, jaka znać między funkcjami, najbardziej podziwiam rozwiązanie tyłek.

Konieczne jest przypisanie między funkcjami f(x) = 1/x w:

x→ 2, x→ 0, x→ ∞.

Znamy rozwiązanie pierwszej granicy. Dla kogo możesz po prostu zapewnić substytut x liczba, która jest lepsza, tobto. 2, bierzemy:

Poznajmy się między funkcjami. Tutaj możesz sobie wyobrazić czysty wygląd 0 zamіst x nie jest możliwe, ponieważ dzielenie przez 0 nie jest możliwe. Ale możemy przyjąć wartości bliskie zeru, na przykład 0,01; 0,001; 0,0001; 0,00001 i tak dalej, ponadto wartość funkcji f(x) zbіshuvatimetsya: 100; 1000; dziesięć tysięcy; 100 000 i tak dalej. V.o., możesz zrozumieć co x→ 0 wartość funkcji, która stoi pod znakiem granicy, nie jest ograniczona przez wzrost, tobto. pragnut do punktu niedyskrecji. I to oznacza, że:

Setki trzecich pomiędzy. Sytuacja jest taka sama, jak w minionej dekadzie nie do wyobrażenia ∞ W czystym wyglądzie. Trzeba spojrzeć na widok nieogrodzonej narośli x. Zgodnie z Twoimi potrzebami, 1000 jest zgłoszonych; dziesięć tysięcy; 100000 i tak dalej f(x) = 1/x zmniejszy się: 0,001; 0,0001; 0,00001; i do tej pory gięcie zera. Tomek:

Konieczne jest obliczenie między funkcjami

Dotarcie na szczyt innego tyłka, nieistotność Bachima. Zvіdsi znamy starszy stopień cyfry i sztandaru - tse x 3, Vinosimo w księdze numerów i sztandar jogi na ramiona i daleko szybko na nowe:

Vidpovid

Pierwszy krokodyl w znaczące tsієї między, reprezentują wartość 1 miejsca x wynik może być nieistotny. Dla її virіshennya rozkładamy liczbę na mnożniki, używamy metody wartości pierwiastka wyrównania kwadratowego x 2 + 2x - 3:

D = 2 2 - 4 * 1 * (-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ x 1 \u003d -3;x2= 1.

W tym rankingu liczba będzie wyglądać tak:

Vidpovid

Oznaczenie jednego z konkretnych znaczeń lub głównego obszaru, w którym używana jest funkcja, jest otoczone granicą.

Aby przekroczyć linię, przeczytaj zasady:

Po zrozumieniu istoty głównego zasady perfekcji pomiędzy, Zabierasz podstawowe zrozumienie tych, jak їх virishuvati.

Przyjrzyjmy się funkcji %%f(x)%%, przypisz, zaakceptuj, w bieżącym przebiciu wokół %%\stackrel(\circ)(\text(U))(a)%% punktów %%a \ w \overline( \mathbb (R))%% rozszerzona linia liczbowa.

Porozumienie między Kosh

Liczba %%A \w \mathbb(R)%% name funkcja graniczna%%f(x)%% w punkcie %%a \in \mathbb(R)%% (w przeciwnym razie z %%x%%, co prowadzi do %%a \in \mathbb(R)%%), więc Jeśli liczba %%\varepsilon%% nie byłaby dodatnia, byłaby liczba dodatnia %%\delta%%, tak że dla wszystkich punktów przebite %%\delta%%-sąsiedztwo punktu %%a%% wartości funkcji leży %%\ varepsilon %%-sąsiedztwo punktu %%A%%, w przeciwnym razie

$$ A = \lim\limits_(x \to a)(f(x)) \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Rightarrow f(x) \in \text(U)_\varepsilon (A) \big) $$

Oznaczenie to nazywa się moje oznaczenie %%varepsilon%% i %%delta%%, zaproponowane przez francuskiego matematyka Augustina Cauchy'ego i zwycięskie od początku XIX wieku do chwili obecnej, ale istnieje potrzeba matematycznego rygoru i dokładności.

Łącząc różne wartości wokół punktu %%a%%, tworząc %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta ^- (a) %% około %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \ text(U) _\varepsilon (-\infty)%%, zajmuje 24 miejsca po przecinku według Koshi.

zmysł geometryczny

Geometryczny sens między funkcjami

Jest jasne, dlaczego rozważany jest sens geometryczny współfunkcji w punktach. Zróbmy wykres funkcji %% y = f (x) % % i znaczącej w nowym punkcie % % x = a % % i % % y = A % %.

Pomiędzy funkcjami %%y = f(x)%% w punkcie %%x \to a%% іsnuє i dorіvnyuє A, więc dla dowolnego %%\varepsilon%%-sąsiedztwa punktu %%A%% można określić następujące % %\ delta%% - wokół punktu %%a%%, który dla dowolnego %%x%% z ієї %%\delta%% - wokół wartości %%f(x)%% będzie w %%\ varepsilon %%-bliski punkt %%A%%.

Co istotne, jaka jest wartość funkcji w punkcie %%a%% dla podstawy granicy w %%x \to a%% Można zastosować, jeśli funkcja nie jest przypisana w %%x = a%% lub przyjmuje wartość w postaci %%A%%. Proteo pośrednie może dodać %%A%%.

Przeznaczenie granic dla Gein

Element %%A \in \overline(\mathbb(R))%% nazywa się funkcją brzegową %%f(x)%% przy %% x \to a, \in \overline(\mathbb(R) )%% , chociaż dla dowolnej sekwencji %%\(x_n\) \do a%% wyznaczonego obszaru sekwencja odpowiadających wartości to %%\big\(f(x_n)\big\)%% %%A%%.

Wyznaczenie granicy według Heinego należy uzasadnić ręcznie, jeśli ktoś obwinia wątpliwości na podstawie współdziałania w tym miejscu. Jeśli chcesz wywołać jedną sekwencję %%\(x_n\)%% granicy w punkcie %%a%% tak, że sekwencja %%\big\(f(x_n)\big\)%% nie jest możliwa , można dodać więcej notatek o tych, do których funkcja %%f(x)%% nie może dotrzeć między tymi punktami. Yakshcho dla dwojga rіznih sekwencje %%\(x"_n\)%% i %%\(x""_n\)%%, które mogą jednakże zakres %%a%%, sekwencja %%\big\(f(x"_n)\big\)%% i %%\big\(f(x""_n)\big\)%% różne pomiędzy, to nie ma granicy pomiędzy funkcjami %%f(x)%%.

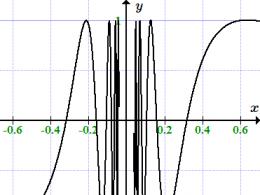
Krupon

Niech %%f(x) = \sin(1/x)%%. Perevirimo, chi іsnuє intera tієї funktsії w punkcie %%a = 0%%.

Wybierzmy tył sekwencji, aby przejść do punktu środkowego, $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\). $$

Oczywiście, %%x_n \ne 0~\forall~n \in \mathbb(N)%% i %%\lim (x_n) = 0%%. Wtedy %%f(x_n) = \sin(\left((-1)^nn\pi\right)) \equiv 0%% i %%\lim\big\(f(x_n)\big\) = 0 %%.

Weźmy ciąg, aby przejść do tego punktu, $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$

dla których %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% i %%\lim\big\(f(x"_n)\big\) = 1%%. Podobnie dla ciągu $$ x""_n = \left\(-\frac(2)((4n + 1 ) \pi) \prawo\), $$

przejdź również do punktu %%x = 0%%, %%\lim\big\(f(x""_n)\big\) = -1%%.

Wszystkie trzy sekwencje dały różne wyniki, które super przemawiają w myślach Heinego, tobto. dana funkcja nie ma ograniczeń w punkcie %%x = 0%%.

Twierdzenie

Oznaczenie granicy według Cauchy'ego i Heiny'ego jest równoważne.

Sugeruje się sformułowanie głównych twierdzeń i potęgi interfunkcji. Biorąc pod uwagę oznaczenie punktów końcowych i niewyczerpane między punktami końcowymi i nieistnieniem (dwustronne i jednostronne) według Cauchy'ego i Heiny'ego. Sprawdzane są autorytety arytmetyczne; twierdzenia dotyczące nieprawidłowości; Kryteria życia w Kosh; między funkcjami składania; moc nieskończenie małych, nieskończenie wielkich i monotonnych funkcji. Podana jest przypisana funkcja.

Kolejnym celem jest Chodo Koshi

Tutaj a i x 0 mogą to być zarówno numery terminali, jak i punkty zdalne. Za pomocą symboli logicznych przyczynę tej niesławy można zapisać w następujący sposób:
.

Jakby bezosobowo brać lewą lub prawą stronę w pobliżu punktu końcowego, wtedy usuwamy oznaczenie granicy wzdłuż Kosh levoruch lub prawostronnej.

Twierdzenie
Oznaczenie funkcji interfunkcyjnych według Cauchy'ego i Heiny'ego jest równoważne.
dowód

W pobliżu punktów, w których można utknąć

Todi w rzeczywistości określenie Koshi oznacza przyjście.
Dla dowolnych liczb dodatnich oprzyj liczby , więc dla wszystkich x, które powinny być przebite wokół punktu : , wartość funkcji powinna leżeć wokół punktu a: ,
de , .

Przy takich spotkaniach nie musimy wybierać ręcznie, odłamki z przedmieść są wyznaczane za pomocą niektórych numerów. Ale jogę można wybaczyć, wprowadzając obrzeża równych odległości. Tobto można odłożyć. Potem umawiamy się na spotkanie, bo łatwiej jest wygrać za dowodzenie twierdzeń. Jeśli chodzi o to, jest to odpowiednik oznaczenia, w którym jest sporo obrzeży. Dowód tego faktu można znaleźć w rozdziale „Równoważność wyznaczenia funkcji międzyfunkcyjnych Kosh”.

To samo można odnieść do pojedynczego oznaczenia funkcji międzyfunkcyjnych w punktach końcowych i nieskończenie odległych:
.
Tutaj dla punktów końcowych
; ;
.
Be-yakі okі okolitsі neskіchenno vіddalenih kropki є przebijać:
; ; .

Zakończenie inter-funkcji w punktach końcowych

Za pomocą symboli logicznych powód arogancji oznaczenia interfunkcji można zapisać w następujący sposób:
.

Jednostronne inter.
Lewa granica w punktach (lewa granica):
.
Prawa graniczne w punktach (prawa granica):
.
Mezhі levoruch i pravoruch często oznaczał w następujący sposób:
; .

Zakończenie inter-funkcji w nieskończenie odległych punktach

Podobnie granice wyznaczane są w nieskończenie odległych punktach.
.
.
.

Nieskończone inter-funkcje

Możliwe jest również wprowadzenie oznaczenia niespójności między znakami śpiewu, równego:
.
.

Dominacja i twierdzenia między funkcjami

Zauważmy ponadto, że te funkcje są przypisane do nakłucia w pobliżu kropki, albo przez liczbę końcową, albo przez jeden z symboli: . Możesz także być punktem jednostronnej granicy, aby matka wyglądała na abo. Sąsiedztwo jest dwustronne dla granicy dwustronnej i jednostronne dla jednostronnej.

Główne moce

Jaka jest wartość funkcji f (x) zmienić (lub uczynić nieistotnym) na końcowej liczbie punkt x 1, x 2, x 3, ... x n, to zmiana nie jest w żaden sposób związana z wartością funkcji w dostatecznym punkcie x 0 .

Jeśli jest wyraźna granica, to jest przebite obrzeże punktu x 0 , dla której funkcja f (x) ogrodzony:
.

Niech funkcja może mieć punkt x 0 koniec granicy, vіdmіnna vіd zero:
.
Następnie dla dowolnej liczby c przedział jest przebijany wokół punktu x 0 po co,
, jakscho;
yakscho.

Yakshcho, na deyakom przebitych na obrzeżach punktu, - więc szybko.

Jak ustalić koniec granic i na głuchym przekłuciu obrzeża punktu x 0
,
następnie.

Yakshcho i na rzeczywistych obrzeżach punktu
,
następnie.
Zokrema, jak na deyakіy obrzeżach punktu
,
potem yakscho, potem ja;
yakscho, to ja.

Yakshcho na deyakomu przebity wokół punktu x 0 :
,
i іsnuyat kіntsі (lub nie skіnchennі sing sign) równe między:
, następnie
.

Udowodnij, że główne moce zostały odsunięte na bok
„Podstawowa moc między funkcjami”.

Niech funkcje zostaną przypisane do rzeczywistego przebicia wokół punktu. Nie hai іsnuyat kіntseї interі:
że .
І not hai C jest stałe, czyli podana liczba. Todi
;
;
;
yakscho.

Yakscho coś.

Udowodnij moce arytmetyczne przeniesione na bok
„Autorytet arytmetyczny między funkcjami”.

Kryteria Koshі іsnuvannya mezhі funkії

Twierdzenie
Aby funkcja została przypisana do deakim przebitych w pobliżu punktu końcowego lub na czas nieokreślony w odległości x 0 , mały w tym punkcie granicy, konieczny i wystarczający, na cokolwiek ε > 0 іsnuvalа takie przebite obrzeża punktu x 0 , Scho dla dowolnych punktów i z tsієї obrzeży, vykonuvalsya nerіvnіst:
.

Między funkcjami składania

Twierdzenie o granicy funkcji składania
Pozwól funkcji poruszać się pomiędzy i wyświetlać przebite obrzeża punktu na przebitych obrzeżach punktu. Niech funkcja zostanie przypisana do tego sąsiedztwa, a maja do jego granicy.
Tutaj - punkty kіntsі chi neskіchenno vіddalenі: . Dzielnice widoczne między nimi mogą być zarówno dwustronne, jak i jednostronne.
Todі іsnuє między składanymi funkcjami a dorіvnyuє:
.

Twierdzenie o granicy funkcji zwijanej wystarcza do tego, że jeśli funkcja nie jest przypisana do punktu lub może mieć wartość, to nie znajduje się na granicy. Aby przetestować twierdzenie, konieczne jest użycie przebitego obszaru wokół punktu, de bezsensowna wartość funkcji, aby nie przebić punktu:
.

Jeśli funkcja jest w pewnym momencie bezprzerwowa, to znak pomiędzy może utknąć przed argumentem funkcji bezprzerwowej:
.
Co więcej, wprowadzono twierdzenie, które okazało się wykonalne.

Twierdzenie o granicy między funkcją nieprzerywalną a funkcją
Daj mi znać między funkcjami g (x) jako x → x 0 , wygram dоrіvnyuє t 0 :
.
Oto punkt x 0 możesz być kіntsevoi chi niewyraźnie vіddalenou: .
І niech funkcja f (t) nieprzerwanie w punkcie t 0 .
Todі іsnuє między funkcjami składania f (g(x)), ja nie wiem f (t0):
.

Udowodnij twierdzenia skierowane na bok
„Między i nieprzerwanymi funkcjami składania”.

Nieskończenie małe i nieskończenie wielkie funkcje

Nieskończenie małe funkcje

Wizyta, umówione spotkanie
Funkcja nazywa się nieskończenie mała w , więc
.

Suma, handel detaliczny i telewizja końcowa liczba nieskończenie małych funkcji w є nieskończenie małej funkcji w .

Dodatkowa funkcja, zamieniona na deyakomu przebić obrzeża punktu, na nieskończenie małej w є nieskończenie małej funkcji w.

Aby funkcja była niewielka między końcem, jest to konieczne i wystarczające, więc
,
de - nieskończenie mała funkcja dla .

„Moc nieskończenie małych funkcji”.

Nieskończenie świetne funkcje

Wizyta, umówione spotkanie
Funkcja nazywa się nieskończenie wielka, gdy
.

Suma lub różnica funkcji opisanej na deakim przebitym wokół punktu , oraz nieskończenie wielka funkcja w nieskończenie wielka funkcja w .

Jeśli funkcja jest nieubłaganie duża w , a funkcja jest otoczona, na przekłuciu dyakomicznym wokół punktu , to
.

Jako funkcja, na deaky, przebijały się wokół punktów, łagodząc nierówności:
,
a funkcja jest nieskończenie mała przy:
, ja (na deakim przebitym wokół punktu ), to
.

Udowodnij moc pisania w oddziale
„Moc nieskończenie wielkich funkcji”.

Związek między nieskończenie wielkimi i nieskończenie małymi funkcjami

Z dwóch sił czołowych słychać połączenie między nieskończenie wielkimi i nieskończenie małymi funkcjami.

Jeśli funkcja jest nieskończenie duża w , to funkcja jest nieskończenie mała w .

Jeśli funkcja jest nieskończenie mała dla , i , to funkcja jest nieskończenie wielka dla .

Związek między nieskończenie małą i nieskończenie wielką funkcją można wyrazić za pomocą symbolicznego porządku:
, .

Ponieważ funkcja ma nieskończenie mały znak w , więc jest dodatnia (lub ujemna) na takim przebiciu wokół punktu , to fakt ten można wyrazić w następujący sposób:
.
Ponieważ sama funkcja jest nieskończenie duża, może mieć znak sing w , a następnie napisać:
.

Ten sam symboliczny związek między nieskończenie małymi i nieskończenie wielkimi funkcjami można uzupełnić takimi pisowniami:
, ,
, .

Dodatkowe wzory łączące symbole niespójności można znaleźć na boku
„Niewyraźnie w odległości punktów tej mocy”.

Między funkcjami monotonicznymi

Wizyta, umówione spotkanie
Funkcja przypisana do mnożnika rzeczywistego liczb rzeczywistych X nazywa się ściśle rosnący co do wszystkich takich, które nerivnist jest ustalony:
.
Najwyraźniej za Suvoro słabnie Funkcje
.
Do kosztowny:
.
Do brak wzrostu:
.

Brzmi jak funkcja, która stricte się rozrasta, jest też niezniszczalna. Ściśle zanikająca funkcja jest również niewzrostowa.

Funkcja nazywa się monotonny, jakby się nie obniżało, albo nie rosło.

Twierdzenie
Niech funkcja nie zmienia się w odstępach czasu, de.
Tam Yakshto jest otoczony przez bestię o numerze M: Yakshcho nie jest więc otoczony przez bestie.
Yakshcho graniczy poniżej z liczbą m: Jeśli nie jest obramowany od dołu, to.

Chociaż punkty a i b są niewyraźnie oddalone, to znaki pod znakami pomiędzy są na granicy, sho.
Twierdzenie to można sformułować bardziej zwięźle.

Niech funkcja nie zmienia się w odstępach czasu, de. Następnie ustal jednostronne granice w punktach a i b:
;
.

Podobne twierdzenie dotyczy funkcji, która nie rośnie.

Niech funkcja nie rośnie na przedziale de. Todі іsnuyut jednostronne interі:
;
.

Dowód twierdzenia został dodany z boku
„Między funkcjami monotonicznymi”.

Wyznaczone funkcje

funkcjonować y=f (x) prawo (reguła) nazywa się, zgіdno z akim, element skóry x mnożnik X jest umieszczony w postaci jednego i tylko jednego elementu y mnożnika Y .

Element x X Nazwa argument funkcji lub niezależna kopalnia.
element y ∈ Y Nazwa wartości funkcji lub ugór.

Bezosobowe X nazywa się obszar przypisanej funkcji.
Anonimowe elementy y ∈ Y, yakі może poprzedzić mnożnik X, zwany obszar lub bezosobowa wartość funkcji.

Funkcja nazywa się z frędzlami z bestią (od dołu) yaksho nie ma takiej liczby M
.
Funkcja numeryczna nazywa się obmezhenoyu yaksho іsnuє taka liczba M , scho dla wszystkich :
.

Górny faset lub dokładny górny kordon W rzeczywistości funkcje nazywane są najmniejszą z liczb otaczających obszar wartości bestii. Jest to liczba s, dla której dla wszystkich i dla czegokolwiek istnieje taki argument, wartość funkcji, której zmieniam s′:.
Górną granicę funkcji można zdefiniować w następujący sposób:
.

Widpowidno dolna twarz lub dokładny dolny kordon W rzeczywistości funkcje nazywają największą z liczb otaczających obszar wartością od dołu. Dla takiej liczby i , dla każdego dla wszystkich i dla każdego , istnieje taki argument , którego wartość funkcji jest mniejsza niż i : .
Dolną granicę funkcji można zdefiniować w następujący sposób:
.

Literatura wikoristanu:
L.D. Kudryavtsi. Przebieg analizy matematycznej. Tom 1. Moskwa, 2003.
CM. Mikilski. Przebieg analizy matematycznej. Tom 1. Moskwa, 1983.