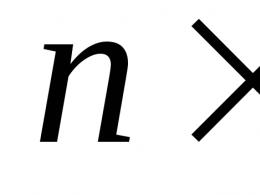Grupy cykliczne. Podgrupy cykliczne Liczba elementów, które są generowane w grupie cyklicznej
Podgrupy grup cyklicznych
Nadchodzi twierdzenie, które definiuje istnienie podgrupy grup cyklicznych.
Twierdzenie 1.4. Podgrupa grupy cyklicznej jest cykliczna. Yakscho G = (a)uH - niesamodzielna podgrupa grupy G, moH = (i P), de P - najmniejsza liczba naturalna, taka jak a p e N.
Dowód. No dalej G = (a) to H- podgrupa grupy G. Jak podgrupa H singiel, więc H =(f) – grupa cykliczna. Dalej H- podgrupa niesamodzielna. Znacząco przez P najmniejsza liczba naturalna, więc długopis, i daj nam znać, że H \u003d (p). Włączenie ( PI) h H oczywiście. Włączmy to. Dalej h e H. Oskilki G = (a), to jest prawdziwy show zanim, Więc co h = k. Podilimo zanim na P za dużo: zanim = nq+ g, de 0 pkt. g F 0, to weź h = a do = a pa p h a g, gwiazdy a r \u003d a ~ p hN e N. Doszedł do doskonałości z minimalnym wyświetlaczem P. Również r = 0 i do - nq. Zwіdsi h = a k = a p h e a"). W tej randze H h ( a n), później, H = (a mi). Twierdzenie zostało zakończone.
Generowanie elementów grupy cyklicznej
Jakie pierwiastki mogą dać początek grupie cyklicznej? Istnieją dwa zaawansowane twierdzenia.
Twierdzenie 1.5. Niech grupa cykliczna G = (a) otrzyma niezredukowany porządek. Todi (a) - (a do) wtedy i tylko wtedy, jeśli do - ± 1.
Dowód. Dalej G = (a),|a| = ° ° i (a) = (Ak). Todі іsnuє tіla kіlkіst P, Więc co a = kp. Zvіdsi a * "-1 \u003d mi, i oskolki | a = następnie kp - 1 = 0. Alethodi kp = 1 ich-± 1. Poważna twardość jest oczywista.
Twierdzenie 1.6. Podajmy grupę cykliczną G = (a) rzędu m. gcd(/s, t) = 1.
Dowód.(=>) No dalej (a) = (a przed), daj nam znać, że GCD(/s, t) - 1. Znacząco SNDC, t) – re. Oskilki a mi (a) - (a do), następnie a = kp z obecną całością P. Dla dokładnej kolejności elementów gwiazdy śpiewają, scho (1 - kp) : t, Tobto. jeden - kp = mt dla liczby całkowitej t. Ale todi 1 = (kp + mt) : d, gwiazdki d = 1 w GCD (/s, t)= 1.
(Chodźmy NID (k, t) = 1. Dowiedzmy się co (a) = (Ak). Ogłoszenie (a przed) h (a) jest oczywiste. Z powrotem, myśl BOGA#, t) = 1 kolejne numery і i v, takie Ki + mw= 1. Koristuyuchis tim sho | | - t, do przyjęcia a = a ku + mv = a ku a mv = a kі e (a to). Otzhe, (a) = (a do). Twierdzenie zostało zakończone.
Zgadnij co Funkcja Eulera f(t) oznacza liczbę liczb naturalnych, która nie zmienia liczby naturalnej t i wzajemnie proste tych. Musimy ponieść konsekwencje.
Ostatni, ubiegły, zeszły. Grupa cykliczna (a) zamówienie t maє f(t) różnych elementów, które są generowane.
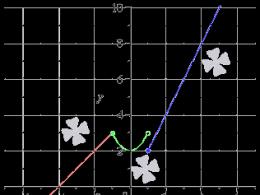
Dla danej dokładności geometrycznej Twierdzenia 1.5 reprezentujemy grupę cykliczną G = (a) zamówienie t stawiać punkty A 0, A b ..., A t _ b podziel to na t równe części. element do podane grupy, które pokazują punkty A wcześniej wygeneruje niektóre i tylko niektóre, jeśli kolejno punkty A 0, A do, A 2k itd., dojdziemy do punktu A]. Dowiedzmy się wszystkiego zanim w t= 10 po prostu wyliczmy vipadkіv (ryc. 1.5). W rezultacie bierzemy przed =1,3, 7, 9. Dla grupy cyklicznej (a) tse oznacza, że (a) \u003d (a 3) \u003d (a 7) \u003d (a 9). powrót: wiem zanim, wzajemnie proste z tym samym numerem t, możesz łaskawie vikreslyuvat vodpovidnu „mała gwiazdka”, mocno wiedząc, że wcześniej wypijesz chi pizno w punkcie skóry, więcej (a) \u003d ( a do).
Niech g będzie dodatkowym elementem grupy G. Todi, przyjmując podgrupę minimalną  , generowany przez jeden element
, generowany przez jeden element  .
.
Wizyta, umówione spotkanie.
Minimalna podgrupa  , generowany przez jeden element g grupy G, nazywa się podgrupa cykliczna grupa G.
, generowany przez jeden element g grupy G, nazywa się podgrupa cykliczna grupa G.
Wizyta, umówione spotkanie.
Tak jak grupa G rodzi się z jednego elementu, czyli.  , to nazywa się grupa cykliczna.
, to nazywa się grupa cykliczna.
Dalej  element grupy multiplikatywnej G, ta sama podgrupa minimalna, generowana przez ten element, jest tworzona z tego elementu
element grupy multiplikatywnej G, ta sama podgrupa minimalna, generowana przez ten element, jest tworzona z tego elementu

Spójrzmy na krok elementu  , następnie. elementy
, następnie. elementy
 .
.
Dwie możliwości:
1. Element kroku Usі g raznі, tobto. 
 , to tutaj powiem, że element g nie może być redukowany w kolejności.
, to tutaj powiem, że element g nie może być redukowany w kolejności.
2. Є kroki zbіgi, tobto. , ale  .
.
І tutaj element g jest ostatecznym porządkiem.
Dobrze, powiedz mi na przykład,  і
і  Todi,
Todi,  , następnie. ustal pozytywne kroki
, następnie. ustal pozytywne kroki  element
element  , równy jednemu elementowi.
, równy jednemu elementowi.
Niech d - najmniej dodatni wskaźnik poziomu pierwiastka  , dla którego
, dla którego  . Wtedy wydaje się, że żywioł
. Wtedy wydaje się, że żywioł  Maj ostatnie zamówienie, równe d.
Maj ostatnie zamówienie, równe d.
Visnovok.
Mieć rodzaj grupy G ostatniego rzędu (  ) wszystkie elementy będą w ostatecznej kolejności.
) wszystkie elementy będą w ostatecznej kolejności.
Niech g będzie elementem grupy multiplikatywnej G lub podgrupy multiplikatywnej  sumuje się ze wszystkich etapów elementu g. Otzhe, liczba elementów w podgrupie
sumuje się ze wszystkich etapów elementu g. Otzhe, liczba elementów w podgrupie  zbigaєtsya z kolejnością elementu
zbigaєtsya z kolejnością elementu  Tobto.
Tobto.
liczba elementów w grupie  kolejność jednego elementu
kolejność jednego elementu  ,
,
 .
.
Z drugiej strony może być ta sama twardość.
Jędrność.
Zamówienie  bez względu na żywioł
bez względu na żywioł  do rzędu minimalnej podgrupy generowanej przez ten element
do rzędu minimalnej podgrupy generowanej przez ten element  .
.
Dowód.
1.Yakscho  - Element ostatecznego zamówienia
- Element ostatecznego zamówienia  , następnie
, następnie
2. Yakscho  - Element niespójnego porządku, a potem nic nie wnosić.
- Element niespójnego porządku, a potem nic nie wnosić.
Element Yakscho  może zamówić
może zamówić  , to w tym celu wszystkie elementy
, to w tym celu wszystkie elementy

inny i być krokiem  zbіgaєtsya z jednym z tych elementów.
zbіgaєtsya z jednym z tych elementów.
To prawda, niech ostentacyjny krok!  , następnie.
, następnie.  - wystarczy numer i nie idź
- wystarczy numer i nie idź  . Ten sam numer
. Ten sam numer  widać na pierwszy rzut oka
widać na pierwszy rzut oka  , de
, de  ,
, . Todі, vikoristuuuuuuuuuuuu poziom mocy elementu g,
. Todі, vikoristuuuuuuuuuuuu poziom mocy elementu g,
 .
.
Zokrema, Yakshcho.
krupon.
Dalej  - Abelowa grupa liczb całkowitych jest addytywna. Grupa G składa się z minimalnej podgrupy, generowanej przez jeden z elementów 1 lub –1:
- Abelowa grupa liczb całkowitych jest addytywna. Grupa G składa się z minimalnej podgrupy, generowanej przez jeden z elementów 1 lub –1:

 ,
,
otzhe,  - Grupa Bezkіnechna tsiklіchna.
- Grupa Bezkіnechna tsiklіchna.
Grupy cykliczne ostatecznej kolejności
Jak przykład cyklicznej grupy ostatniego rzędu, jest to jasne grupa owijająca właściwe n-kutnik shodo yogo do środka  .
.
Elementy grupy
є obróć n-kutnik przeciwko strzałce godinnikova na kuti
Elementy grupy
 є
є
 ,
,
a z odbicia geometrycznego jasno wynika, że

 .
.
Grupa  zemścić się na żywiołach, tobto.
zemścić się na żywiołach, tobto.  , ale satysfakcjonujący element grupy
, ale satysfakcjonujący element grupy  є
є  , następnie.
, następnie.
 .
.
Dalej  todi (dział rys. 1)
todi (dział rys. 1)

Ryż. jeden –
Grupa  - opakowanie prawidłowego trikutnika ABC shodo do środka O.
- opakowanie prawidłowego trikutnika ABC shodo do środka O.
Operacja algebraiczna w grupie  - Ostatnie owinięcie przeciwko strzałce roku, na kut, wielokrotność
- Ostatnie owinięcie przeciwko strzałce roku, na kut, wielokrotność  , następnie.
, następnie.
Zvorotny element  - zawijanie za strzałką roku na kut 1, tobto.
- zawijanie za strzałką roku na kut 1, tobto.
 .
.
Tabela Kmichi
Analiza grup kіntsevyh najbardziej bezpośrednio zdіysnyuvati z tabel podmogoyu Keli, є є zagalnennym vіdomoї "tablice mnożenia".
Niech grupa G zemści się na elementach n.
Moim zdaniem stół Keli є macierz kwadratowa jest n wierszy i n wierszy.
Do rzędu karnacji i warstwy karnacji jeden lub więcej niż jeden element grupy.
element  tabela Kelі, scho, aby stanąć na siatkówce i-tego rzędu i j-tej kolumny, do wyniku operacji „mnożenia” i-tego elementu z j-tym elementem grupy.
tabela Kelі, scho, aby stanąć na siatkówce i-tego rzędu i j-tej kolumny, do wyniku operacji „mnożenia” i-tego elementu z j-tym elementem grupy.
Krupon. Niech grupa G pomści trzy elementy (g 1, g 2, g 3). Działanie w grupie „mnożenie”. W tym momencie stół Keli może wyglądać:

Szacunek. W rzędzie skin i kolumnie skin tabeli Keli znajdują się wszystkie elementy grupy i nie ma smrodu. Tabela Keli do zastąpienia wszystkich informacji o grupie. Co możesz powiedzieć o sile tej grupy?
1. Jedynym elementem tej grupy jest g1.
2. Grupa jest abelowa, ponieważ stół jest symetryczny wzdłuż głównej przekątnej.
3. W przypadku elementu skóry grupy konieczne jest:
dla g 1 okład є element g 1 dla g 2 element g 3 .
Chodźmy na grupy  Tabele komórek.
Tabele komórek.

Dla znaczenia kluczowego elementu dla elementu, na przykład,  , jest to konieczne z rzędu, co jest wymagane dla elementu
, jest to konieczne z rzędu, co jest wymagane dla elementu  znać element zemsty piecyków
znać element zemsty piecyków  . element
. element  vidpovіdny przekazany stovptsyu i є vorotnym do elementu
vidpovіdny przekazany stovptsyu i є vorotnym do elementu  , ponieważ
, ponieważ  .
.
Podobnie jak stół Keli jest symetryczny jak przekątna głowy, tse oznacza, że

- Tobto. działanie grupy jest przemienne. Dla wywodu, tabela Keli jest symetryczna, chociaż przekątna głowy oznacza, że operacja jest w  to znaczy przemienne.
to znaczy przemienne.  ,
,
Grupa  - Abiełowa.
- Abiełowa.
Widać całą grupę przekształceń symetrii poprawnego n - cosin  po dodaniu do operacji zawinięcia dodatkowej operacji przestrzennego zakrętu wokół osi symetrii.
po dodaniu do operacji zawinięcia dodatkowej operacji przestrzennego zakrętu wokół osi symetrii.
Dla trikutnika  i grupa
i grupa  zemsta sześciu żywiołów
zemsta sześciu żywiołów
de  Skręć Tse (div. small. 2) na odpowiednią wysokość, medianę, bisekcję i może wyglądać:
Skręć Tse (div. small. 2) na odpowiednią wysokość, medianę, bisekcję i może wyglądać:
 ;
;
 ,
,
,
 .
.


Ryż. 2.- Grupa  - Zmiana symetrii regularnego trykotu ABC.
- Zmiana symetrii regularnego trykotu ABC.
Bagato, otrimane w wyniku tego procesu, pojawia się w tekście jako . Zdobywanie szacunku jest tym samym, co 0 = e.
Zdjęcie 5,7
3 grupy G =< Z 6 , +>Can buti otrimani chotiri cykliczne podgrupy. Tse H1 =<{0},+>, H2 =<{0, 2, 4}, +>, H 3 =<{0, 3}, +> і H 4 \u003d G. Z szacunkiem, jeśli operacja jest dodatkiem, to n oznacza pomnożenie n przez a. Warto również zauważyć, że we wszystkich tych grupach operacja polega na dodaniu modułu 6. Poniżej pokazano, jak znane są elementy tych podgrup cyklicznych.
a. Podgrupa cykliczna, generowana z 0 - ce H 1 tylko jeden pierwiastek (pierwiastek neutralny).
b. Podgrupa cykliczna, generowana na podstawie 1, - ce H4, jak sama grupa G.
1 0 mod 6 = 0 1 1 mod 6 = 1 1 2 mod 6 = (1 + 1) mod 6 = 2 1 3 mod 6 = (1 + 1 + 1) mod 6 = 3 1 4 mod 6 = (1 + 1 + 1 + 1) mod 6 = 4 1 5 mod 6 = (1 + 1 + 1 + 1 + 1) mod 6 = 5
w. Podgrupa cykliczna, generowana na podstawie 2 - tse H 2 i może mieć trzy elementy: 0, 2 i 4.
2 0 mod 6 = 0 2 1 mod 6 = 2 2 2 mod 6 = (2 + 2) mod 6 = 4
d. Podgrupa cykliczna, generowana na podstawie 3 - ce H 3, ponieważ może mieć dwa elementy: 0 i 3.
e. Podgrupa cykliczna, generowana na podstawie 4-H 2 ; tse nie jest nową podgrupą.
4 0 mod 6 = 0 4 1 mod 6 = 4 4 2 mod 6 = (4 + 4) mod 6 = 2
e. Podgrupa cykliczna, wygenerowana na podstawie 5, - ce H 4, wygrała - sama grupa G.
5 0 mod 6 = 0 5 1 mod 6 = 5 5 2 mod 6 = 4 5 3 mod 6 = 3 5 4 mod 6 = 2 5 5 mod 6 = 1
Zdjęcie 5,8
Z grupy można pobrać trzy cykliczne podgrupy. Elementy G maє tilki chotiri: 1, 3, 7 i 9. Podgrupy cykliczne - ![]()
![]() że . Poniżej pokazano, jak znane są elementy podgrupy.
że . Poniżej pokazano, jak znane są elementy podgrupy.
a. Podgrupa cykliczna, generowana na podstawie 1, - ce H1. Podgrupa ma tylko jeden element i sama jest neutralna.
b. Podgrupa cykliczna, generowana na podstawie 3, - ce H3, podobnie jak grupa G.
3 0 mod 10 = 1 3 1 mod 10 = 3 3 2 mod 10 = 9 3 3 mod 10 = 7
w. Podgrupa cykliczna, generowana na podstawie 7, - ce H3, a także grupa G.
7 0 mod 10 = 1 7 1 mod 10 = 7 7 2 mod 10 = 9 7 3 mod 10 = 3
d. Podgrupa cykliczna, generowana na podstawie 9, - ce H2. Podgrupa może składać się tylko z dwóch elementów.
9 0 mod 10 = 1 9 1 mod 10 = 9
Grupy cykliczne
Grupa cykliczna- Grupa, jak suwerenna podgrupa cykliczna. W tyłek 5.7 grupa może mieć cykliczną podgrupę H 5 \u003d G. Tse oznacza, że grupa G jest grupą cykliczną. W jaki sposób element, który generuje cykliczną podgrupę, może również generować grupę. Ten element nosi nazwę „generator”. Podobnie jak g - generator, elementy końcowej grupy cyklicznej można zapisać tak:
(e, g, g 2, ....., g n-1), de gn = e.
Z całym szacunkiem, grupa cykliczna może matkować wiele generatorów.
Zdjęcie 5,9
a. Grupa G =
b. Grupa - cykliczna grupa z dwoma generatorami, g = 3 i g = 7 .
Twierdzenie Lagrange'a
Twierdzenie Lagrange'a pokaż różnicę między porządkiem grupy a porządkiem podgrupy. Załóżmy, że G jest grupą, a H podgrupą G . Podobnie jak kolejność G i H - |G| oraz |H| , ważne, ważne aż do twierdzenia |H| udostępnij | G | . Dla aplikacji 5.7 | G | = 6 . Kolejność podgrup - | h1 | = 1, | H2 | = 3, | H3 | = 2 i |H4| = 6 . Oczywiście wszystkie zamówienia są dilnikami 6 .
Twierdzenie Lagrange'a może być więcej niż kilkoma dodatkami. Jeśli podano grupę G, to її rząd | G | , można łatwo przypisywać zamówienia potencjalnych podgrup, dzięki czemu można poznać dilnika. Na przykład kolejność grupy G =
Kolejność elementów
Kolejność elementów grupa porządkowa (a) (rząd (a)) ma najmniejszą liczbę całkowitą n taką, że a n = e . Innymi słowy: kolejność elementu to kolejność grupy, czyli sposób jej generowania.
Zdjęcie 5.10
a. Grupa G =
b. Grupa G =
- 1. Grupa Z całe liczby z operacji składania.
- 2. Grupa wszystkich złożonych korzeni kroku n od jednego do operacji mnożenia. Izomorfizm liczby cyklicznej Oskilki
grupa jest cykliczna i tworzony jest element.
Mój bachimo, że grupy cykliczne mogą być zarówno endemiczne, jak i niesyntetyczne.
3. No dalej - dobra grupa i dobry żywioł. Bagato to grupa cykliczna z satysfakcjonującym pierwiastkiem g. Nazywa się to cykliczną podgrupą generowaną przez element g, a ta kolejność jest porządkiem elementu g. Zgodnie z twierdzeniem Lagrange'a, rząd elementu jest rozszerzaczem grupy. Fermentacja
co kryje się za formułą:
Najwyraźniej przez homomorfizm ten obraz її to zbіgaєtsya. Vidobrazhennya jest sur'iektywnie taka sama i mniej taka sama, jeśli grupa G- cykliczny g Ustalam element. Który sposób nazywamy standardowym homomorfizmem dla grupy cyklicznej? G ze skręconym skrętem g.
Zastosovuyuchi w ten sposób twierdzenie o homomorfizmie, bierzemy pod uwagę znaczenie mocy grup cyklicznych: czy grupa cykliczna jest rangą homomorficzną. Z .
Miej jakąś grupę G może być wyznaczony krok element z wieloma wskazaniami:
Niech miejsce mocy
Tse oczywiście, yakscho . Spójrzmy na vipadok, jeśli . Todi
Podobnie patrzy się na inne tendencje.
З (6) krzyczeć, sho
Krіm ponadto dla mianowanych. W tej kolejności poziom elementu określa podgrupę grupy G. Vaughn nazywa się podgrupa cykliczna generowana przez element, i jest wskazany przez .
Zasadniczo istnieją dwie możliwe różnice: albo wszystkie etapy elementu są różne, albo nie. W pierwszym typie podgrupa nie jest chuda. Rzućmy okiem na inny aspekt.
Dalej ,; To samo. Najmniej liczb naturalnych t, dla tych, którzy są w ten sposób powołani w celu element i jest wskazany przez .
propozycja 1. Yakscho , następnie
dowód. 1) Dziel m na P za dużo:
Przejdź przez wyznaczone zamówienie
Ze względu na do przodu
Ostatni, ubiegły, zeszły. Yakshcho, podgrupa mo revenge n elementów.
Dowód. Prawdziwe,
ponadto wszystkie elementy są inne.
To ma vipadkę, jeśli nie masz takiej naturalnej t, scho (tobto może być pierwszym z powyższych opisów), vvazhayut . Vіdmitimo, scho; rzędy wszystkich pozostałych elementów grupy są większe niż 1.
W grupie dodatków nie mówimy o stopniu pierwiastka , o jodze wielokrotności yaki oznacza przez . W zależności od kolejności elementu grupy dodatków G- najmniejsza z liczb naturalnych t(jak wiadomo), dla tych
ZASTOSOWANIE 1. Cechą tego pola jest kolejność dowolnego niezerowego pierwiastka w i-tej grupie dodatków.
TYŁ 2. Oczywiste jest, że grupa kіntsevoi ma kolejność dowolnego elementu kіtsevy. Zostanie pokazane, jak obliczane są rzędy elementów w grupie.Zastąpienie nazywa się cykl dozhini i signify przez yakscho wygrywał cyklicznie przearanżować
i reshta w każdym miejscu. Oczywiste jest, że kolejność cyklu jest lepsza nar. Nazywam się cyklami niezależny, nawet wśród liczb, które faktycznie są przez nie przestawiane, nie ma zbyt wielu skandalicznych; w którym kierunku? . Czy to jako substytut, jest to jednoznacznie przedstawione w telewizji niezależnych cykli. Na przykład,
co jest wyraźnie pokazane maleństwu, co przedstawiają strzałki. W ten sposób substytucja jest ułożona w telewizji niezależnych cykli dożynów , następnie
ZASTOSOWANIE 3. Kolejność liczby zespolonej w grupie kіntsevy jest parzysta i sprawiedliwa, jeśli liczba jest korzeniem tego samego świata jedności, więc z własną czernią może być taka sama i tylko wtedy, jeśli porіvnyaєmo z , tobto. .
ZASTOSOWANIE 4. Znamy elementy ostatecznego porządku grupy ruin mieszkania. Dalej. Bo bez względu na to, jaki jest punkt,
obracaj się cyklicznie , więc jaki jest środek ciężkości o niesforne schodo. Otzhe, - lub zwróć się do cięcia umysłu wokół punktu o, w przeciwnym razie powinno być możliwe przejście linii prostej o.
TYŁ 5. Znamy kolejność macierzy
jak element grupy. Maymo
Więc co. Oczywiście ten tyłek jest specjalnie dobrany: zdolność tego, że kolejność sukcesu matrycy będzie ostateczna, bardziej równa zeru.
propozycja 2. Yakscho , następnie
Dowód. Dalej
Więc co. Maymo
Ojciec, .
Spotkanie 1 . Grupa G nazywa cykliczny jak używać takiego elementu , Co . Taki element nazywa się element nadrzędny groupie G.
ZASTOSOWANIE 6. Dodatkowa grupa liczb całkowitych jest cykliczna, odłamki są generowane przez element 1.
ZASTOSOWANIE 7. Dodatkowa grupa wsparcia dla modułu nє cykliczne, odłamki są generowane przez element.
ZASTOSOWANIE 8. Grupa multiplikatywna złożonego pierwiastka n-tego kroku z 1 cyklicznością. Rzeczywiście, podstawowa esencja liczb
To jasne, co . Z tej samej grupy jest generowany przez element.
Łatwo jest bachiti, który jest w niewyczerpanej, cyklicznej grupie pierwiastków, które można wygenerować, tylko kilka. Tak więc w grupie Z elementy rodzicielskie mają więcej niż 1 i - 1.
Liczba elementów w końcowej grupie G o nazwie її w celu jest wskazana przez. Kolejność końcowej grupy cyklicznej jest taka sama jak kolejność generowanego elementu її. Do tego z propozycji 2 płacz
Twierdzenie 3 . Element grupy cyklicznej rząd n generuje trochę i tylko trochę, jeśli
ZASTOSOWANIE 9. Nadrzędne elementy grupy nazywają się podstawowe korzenie n krok od 1. To jest korzeń umysłu , de. Na przykład pierwszy korzeń 12. kroku od 1.
Grupy cykliczne to najprostsze grupy, dzięki czemu możesz się zidentyfikować. (Zwłaszcza smród Abelów.) Kolejne twierdzenie podaje jego nowe opisy.
Twierdzenie 1. Czy grupa nieskończenie cykliczna jest grupą izomorficzną. Bądź jak cykliczna grupa Kіntseva jest w porządku n izomorficzna z grupą.
dowód. Ponieważ jest to nieoskórowana grupa cykliczna, to poprzez wzór (4) jest to izomorfizm.
Chodźmy - grupa kіntseva tsiklіchna w porządku P. Patrzymy na obraz
wtedy wyświetlacz jest prawidłowo przypisany i obiektywnie. moc
viplyvaє іz tієї zh formuła (1). W tym rankingu - izomorfizm.
Twierdzenie zostało zakończone.
Dla zrozumienia bycia grupą ważną rolę odgrywa wiedza o podgrupie. Wszystkie podgrupy grupy cyklicznej można łatwo opisać.
Twierdzenie 2. 1) Bądź podgrupą cyklicznej grupy cyklicznej.
2) Grupa cykliczna jest w porządku n uporządkuj, czy podgrupy mają się dzielić n i dla dowolnej liczby dilnik q n Istnieje dokładnie jedna podgrupa rzędu q.
dowód. 1) Nehai - cykliczna grupa i H- її podgrupa, vіdmіnna vіd (oczywiście pojedyncza podgrupa, cykliczna.) . Dalej t- najmniejsza z liczb naturalnych, dla tych . Daj nam znać, że . Dalej . Podilimo zanim na t za dużo:
gwiazdki z wyznaczonej daty t następny, scho th, później, .
2) Jakscho , potem prześlij mirkuvannya, zastosovane do ), Pokaż co . Z kim
і Hє pojedyncza kolejność podgrup q w grupie G. plecy, jakscho q- bądź dilnikem liczby Pі , potem podwielokrotność H, zrównoważenie vynachaetsya (9), porządek podgrupy q. Twierdzenie zostało zakończone.
Konsekwencja . W grupie cyklicznej o prostym porządku, niezależnie od tego, czy nie jest sama, podgrupa biegnie z drugą grupą.
ZASTOSOWANIE 10. W grupie, czy to podgrupie, mogę patrzeć, de.
ZASTOSOWANIE 11. W grupie pierwiastków n-tego kroku z 1 bądź podgrupą grupy pierwiastków q- krok od 1, de.
Spójrzmy na multiplikatywną grupę wszystkich lub dwóch kroków po dwa (2Z, ), de 2Z = (2n | P eZ). Analogiem grupy addytywnej my є jest grupa addytywna bliźniaczych liczb całkowitych (2Z, +), 2Z = (2n | pe Z). Grupy Damo zagalne vyznachennya, okremi niedopałki takich grup є danі.
Powołanie 1.8. Grupa multiplikatywna (G,) (Grupa dodatków (G, +)) nazywa się cykliczny jakby sumować się z wymaganej liczby kroków (w zależności od liczby punktów) jednego elementu a e G, Tobto. G=(Ap | pe Z) (vіdpovіdno, G - (pa | pe Z)). Oznaczenie: (a), czytać: grupa cykliczna generowana przez element a.
Przyjrzyjmy się temu.
- 1. Końcówka multiplikatywnej nieskalującej grupy cyklicznej może być grupą wszystkich cykli o stałej liczbie całkowitej F±1, wygrana wskazana i r. w taki sposób, i d - (a).
- 2. Końcem multiplikatywnej końcowej grupy cyklicznej jest grupa C pierwiastków n-tego kroku od jednostki. Zgadywanie, że korzeń n-tego kroku jest sam
za formułą e k= cos---hisin^-, de przed = 0, 1, ..., P - 1. Slajd- pp
tak naprawdę, З„ = (е x) = (е x = 1, e x, ef = e 2 ,..., e "-1 =? „_ x). Domyślamy się, że liczby zespolone e do, do = 1, ..., P - 1, są przedstawione za pomocą punktów pojedynczej stawki P równe części.
- 3. Charakterystycznym przykładem addytywnej nieskalującej grupy cyklicznej jest addytywna grupa liczb całkowitych Z, która jest generowana przez liczbę 1, czyli. Z = (1). Geometrycznie pojawia się na widok całych punktów linii numerycznej. W rzeczywistości tak przedstawia się sama grupa multiplikatywna 2 7 - = (2) a z \u003d (a), numer decyla F±1 (podział rys. 1.3). Jakość obrazów omówiono w paragrafie 1.6.
- 4. Vibero w dużej grupie multiplikatywnej G aktywny element a. Wtedy wszystkie cykle etapów elementu spełniają cykliczną podgrupę (a) = (a pp e Z G.
- 5. Można wykazać, że addytywna grupa liczb wymiernych Q sama w sobie nie jest cykliczna, ale niezależnie od tego, czy dwa pierwiastki leżą w podgrupie cyklicznej.
A. Udowadniamy, że grupa dodatków Q nie jest cykliczna. Dopuszczalne niedopuszczalne: niech Q = (-). Podstawowa liczba docelowa b,
nie udostępniaj tych. Oskіlki - eQ = (-) = sn-|neZ>, a następnie istniejący
b t/ (t J
є liczba tsile gs 0, więc - = n 0 -. Ale todi m = n 0 kb
gwiazdy t:- super-ostrość dіyshli.
B. Załóżmy, że dwie dość wymierne liczby -
h „ /1
i - nakładają się na podgrupę cykliczną (-), de tє znaleźć- d t/
mniej niż duża wielokrotność liczb bі d. Racja, nie róbmy tego m-bi
, a 1 /1 h cv 1/1
ja m = śr, u, v e Z, wtedy ja - = - = aї-e(-)i - = - = cv-e(-).
b b ja t t/ a dv t t/
Twierdzenie 1.3. Kolejność grupy cyklicznej jest taka sama jak kolejność elementu macierzystego grupy, tobto.|(a)| = | |.
Dowód. 1. Chodź | = ">. Wiemy, że wszystkie naturalne kroki żywiołu a różne. Dopuszczalne niedopuszczalne: chodź a k = a tі 0 do Todi t - zanim- liczba naturalna a t ~ do = e. Ale tse superechit do tego, scho | a = ° °. W ten sposób wszystkie naturalne kroki żywiołu a raznі, zvіdki vyplivaє neskіchennіst group (a). Otzhe, | (a)| = ° ° = | |.
2. Chodź | | = n. (a) \u003d (e - 0, a, 2,..., a "-1). Od oznaczenia grupy cyklicznej, włączenie (a 0, a, a 2, ..., o" 1-1) s (a). Włączmy to. Dodatkowy element grupy cyklicznej (a) może wyglądać w, de ti Z. Udostępnianie sznapsów w nadmiarze: m-nq + r, de 0 p. Oskilki a n = e, następnie w = a p ja + g \u003d p h? a r = a r e(o 0, o, 2 ,..., "- 1). -1).
Konieczne jest doprowadzenie do pomnożenia wszystkich elementów (a 0, a, 2 ,..., a "-1) różne. Dopuszczalne niedopuszczalne: niech 0 i P, ale a" = a). To samo wino - e ta 0 j - i - dіyshli super-ostrość z umovoy | | = P. Twierdzenie zostało zakończone.