Pokhіdnі vorotnykh trigonometricheskih funktsіy. Vienkāršu trigonometrisko funkciju soļi Uzdevuma apgriezto trigonometrisko funkciju soļi
temats :
Tsіl : formulējiet apgalvojumu par atgriezeniskām trigonometriskām funkcijām.
Pārvaldnieks:
1.
iemācīties zināt šo funkciju līdzības,vingrināties, mācoties atšķirt šīs funkcijas, lai saņemtu palīdzību
patstāvīgs darbs un savstarpēja pārbaude;
2.
attīstīt interesi par matemātiku, skaitīšanu piemiņas iesācēji,
vminnya analizēt citu zinātnieku piedošanu;
3. paaugstināt cieņu, neatkarību
1. Organizatoriskais moments
Es mācu, zinu darba noteikumus stundā, skaidroju, kā pareizi aizpildīt reitingu sarakstu
2. Motivācijas posms
Iemācieties lasīt obov'yazkovo, kāda smirdoņa ir muižniecība un prāts par šo tēmu.
Pirms robota auss apgūstiet noteikumu ATCERIES.
3. Darbības posms
Iemācieties pāriet uz dienas beigām no sākuma lapas (pievienot)
4.Papildu soma nodarbībai
Atspulgs.
Šodien nodarbībā:
ES zināju…
Tas plauka…
Bija grūti...
Man ir bijusi…
ES mēģināšu...
MĀJAS LAPA
pēc tēmas: Pokhіdnі trigonometricheskih un atgriezeniskas trigonometriskās funkcijas.
2 nodarbības.
TĒMU REZULTĀTS IR NEPIECIEŠAMS
ZINĀT: diferenciācijas formula trigonometriskās un apgrieztās trigonometriskās funkcijas.
VMITI: zināt līdzīgas trigonometriskās un reversās trigonometriskās funkcijas.
Pam'yatai , scho treba pratsyuvati aiz algoritma.
Neaizmirstiet iziet pārbaudi, strādāt pie robežatzīmēm, aizpildīt ar tām reitingu sarakstu.
Esi glāsts, neatņem sev to, ko esi ēdis bez palīdzības.
Esiet objektīvs savstarpējās pārbaudīšanas stundā, palīdziet gan jums, gan tam, kuru pārbaudāt.
VEICĀS!
W ADANNA №1
Izlasiet šādas formulas apgriezto trigonometrisko funkciju diferenciācijai: (2 p.)
Tā kā funkcija ir saliekama, tad
de z – elementāra funkcija
Apskatiet piemērus:
y = arcsin(x), tad y/=
y = arcctg(3x 2 -4), tad
y/=
Atrodi labāko:(3 p.)
y= arcsin(-x) y= arctg(-x) y= arcos(2x)
P DOTIES UZ APSKATI №1
W ADANNA №2
Razv'yazhi be — jebkura no lietojumprogrammām: (3b)
a )y = arcos (5x - 3)
b ) y = arcctg(7x+1)
P DOTIES UZ APSKATI №2
W ADANNA №3
a) Skatieties vēlreiz, es izmantošu risinājumu:
b) Atrodiet līdzīgas funkcijas (4 p.)
arcsin (2x 2 - 5x)
arccos (4x 2 - 6x)
P DOTIES UZ APSKATI №3
W ADANNA №4
Labi padarīts! Jūs varat sākt iepriekšpagrieziena robots Nr.1.
ZAVDANNYA №5
a) Paskatieties uz risinājuma aizbāzni:
b) Atrodiet līdzīgas funkcijas (6 p.)
y=
P DOTIES UZ APSKATI №5
Labi padarīts! Jūs varat sākt iepriekšpagrieziena robots Nr.2.
PROVIRKOVA ROBOTS №1
Vikonai viens no variantiem (11b)
1v 2v
1. Iepazīstiet tālāk norādītās funkcijas.
a) 2 punkti
y = arctg(-2x) y = arccos (3x)
b) 4 bumbiņas
y = arcos(3x 2 - 2) y = arcctg(2x 3 +1)
c) 5 punkti
y = arcsin(x 2 - 5x) + iedegums (2x+1) y = arccos(3x 2-2x) + ctg(x+4) maks
bumbiņas
izņemšanu
bumba
PVO
pārlasīšana
novērtējums
1
2 b
3 b
2
3b
3
4b
4
1 1 b
5
6 b
6
1 4 b
uzreiz
43 b
KOPĀ 43 bali
"5" - 33 - 43 bali;
"4" - 24 - 32 bali;
"3" - 18 - 23 Bali.
Viena mainīgā funkcijas diferenciālais aprēķins
1. Ieeja
Matemātiskā analīze ir matemātikas daļa, kas veidojās 18. gadsimtā un ietver divas galvenās daļas: diferenciālos un integrālos aprēķinus. Pokhіdna funkcijas - viena no galvenajām matemātiskajām izpratnēm par diferenciālo aprēķinu. Bagātu matemātiķu (piemēram, I. Ņūtona un R. Leibnica) zinātņu zinātņu vīnu analīzei, kam bija liela loma dabaszinātņu attīstībā - šķiet, ka ir grūti pabeigt universālo risināšanas metodi. funkcijas, kas vaino dažādu lietišķo lietojumprogrammu izstrādes stundu.
2. Ciparu funkcija. Novērošanas funkcijas shēma.
(Skatieties kopsavilkumus par tēmu "Stupinna funktsiya")
1) Piešķirtās funkcijas apgabals.
2) Funkcijas anonīma vērtība.
3) savienošanas pārī, atvienošanas funkcijas.
4) Funkcijas monotonitāte.
5) Apgrieztā funkcija.
6) Nulles funkcijas.
7) Zīmju funkcijas veicināšana.
8) Funkciju apmaiņa.
pa labi:
- Zināt funkcijas apjomu:
a); b); iekšā) 
.
a); b); G).
3. Izpratne starp funkcijām punktā.
Apskatīsim faktisko funkciju grafikus. Pārbaudīsim funkciju uzvedību punkta tuvumā x 0 , tad faktiskajā punkta tuvumā x 0 .
 |
Rīsi. 1. Mazs. 2. Mazs. 3.
Funkcijai var būt jauda, kas ir atkarīga no divām citām funkcijām.
1. Kad arguments ir tuvu X pirms tam x 0 ar kreiso un labo roku ir tādas pašas funkcijas vērtības, kas vienmēr ir tuvu vienam un tam pašam datumam BET.
Divas citas funkcijas nerūpējas par jaudu.
2. Kad arguments ir tuvu X pirms tam x 0 levoruch vіdpovіdnі znachnosti funktsії jaks zavgodno tuvu BET, un kad strīds ir tuvu X pirms tam x 0 ar labo roku, funkcijas vērtības vienmēr ir tuvu AT.
3. Funkcija, kad arguments ir tuvu X pirms tam x 0 kreiļiem un labročiem ir dažādas nozīmes.
Višnovoka: Tāpat kā tad, kad strīds ir tuvu X pirms tam x 0 kreisās un labās puses punkti ar koordinātām vienmēr ir tuvu punktam ar koordinātām, tad.
Muca: Chi maє funkcija robeža punktos x 1, x 2, x 3, x 4, x 5?
 |
Ieteikums: Funkcija maє mezhu punktos x1, x3;
funkcija nepalaidiet garām robežu punktos x2, x4, x5.
Cieņa:
4. Noteikta funkcija bez pārtraukuma punktā un uz līnijas
Funkcijas nepārtrauktības jēdziens ir manuāli saistīts ar apgalvojumiem par funkcijas grafiku kā par “nelineāru” (secīgu) līniju. Ar stingru līniju es cienu līniju, esmu kristīts bez olīvkoka avīzē.
Uzturs: kādas ir šīs funkcijas bez pārtraukumiem?
Rīsi. 1. Mazs. 2. Mazs. 3.
Rīsi. 4. Mazs. 5.
Vidpovіd: Z tsikh funktsіy nepārtraukts є funktіy, izobrazhennaya attēlā. Nr.3, skіlki її grafiks - "neskaidra" (secīga) līnija.
Pārtika: Yak_ iestāde var darboties, parādīts attēlā. Nr.3, un nedomā par citām funkcijām?
Ieteikums:
1. Funkcija tiek piešķirta punktā x 0. Tsya jauda neuzvar funkcijai, kas attēlota attēlā. Nr.1.
2. Rindas beigu pamatfunkcijas punktos x 0. Tsya spēks neuzvar funkcijām, kas attēlotas attēlā. Nr.2, 5.
3. Starp funkcijām punktā x 0 svarīgākā funkcijas vērtība punktā x, tobto 
. Tsya jauda neuzvar funkcijai, kas attēlota attēlā. Nr.4.
Attēlā parādītajai funkcijai izmantotais dominējošais stāvoklis. Nr.3, un dod iespēju punktam piešķirt nepārtrauktu funkciju x 0 .
Pieraksts: funkcija tiek saukta par nepārtrauktu punktā x 0, patīk .
Cieņa: Kā funkcija ir nepārtraukta punktā x 0, tad punkts x 0 sauc par funkcijas nepārtraukšanas punktu, jo funkcija šajā punktā nav nepārtraucama x 0, tad punkts x 0 sauc par funkcijas izplešanās punktu.
Pieraksts:
Funkciju sauc par nepārtrauktu intervālā, jo tā ir nepārtraukta intervāla ādas punktā.
5. Argumentu inkrements, funkcijas pieaugums
Ļaujiet iestatīt funkciju.
x 0 - argumenta pirmā vērtība;
X- argumenta galīgā nozīme;
f (x 0) - funkcijas nozīme;
f(x 0 +D x) - funkcijas pēdējā nozīme.
Pieraksts: Atšķirību starp argumenta galīgo un vālītes vērtību sauc par lielāko argumentu D x \u003d x - x 0
Pieraksts: atšķirību starp funkcijas galīgo un pasta vērtību sauc par lielāko funkciju. D y \u003d f (x 0 + D x) - f (x 0)
Cieņa:
- Ģeometriski palielinot argumentu D x- є funkcijas grafika abscisu punktu atšķirība, kas atbilst argumenta terminālam un vālītes vērtībām.
- Ģeometriski palielināta funkcija D є ordinātu atšķirība ir funkcijas grafika punkti, kas atbilst argumenta gala un vālītes vērtībām.
- Argumenta palielināšanās un funkcijas palielināšanās var būt gan pozitīva, gan negatīva.
6. Saistīto funkciju izpratne. Līdzīgas funkcijas fiziskais sensors
Apskatīsim problēmu par funkciju maiņas ātrumu, de X і plkst var būt kaut kādi fiziski lielumi.
x 0 - argumenta pirmā vērtība; f (x 0) - funkcijas nozīme;
x 0 +D x - argumenta galīgā nozīme; f(x 0 +D x) - funkcijas beigu vērtība;
D y \u003d f (x 0 + D x) - f (x 0) - palielināta funkcionalitāte;
– vidējais funkciju maiņas ātrums intervālos D x .
– mitteva mainīt funkciju, mainīt funkciju punktā x 0.
Pieraksts: citas funkcijas punktā x 0 To sauc par uzlabojumu robežu D funkcijas punktā x 0 uz atveseļošanos D x arguments, kad pragnenny zbіlshennya arguments uz nulli.
Višnovoka: Pohіdna funkcijas punktā x 0є funkcijas maiņas ātrums punktā x 0.
Teorēma: Pohіdna postіynoї funkcijasії y = c ir punkts vienāds ar nulli.
Teorēma: citas funkcijas y = x ir punkts jaukāka vientulība .
.
Cieņa: Līdzīga veida funkcijas nozīmi sauc par diferenciāciju.
7. Summas diferencēšanas noteikumi, izveidošana, privātā funkcija
Apskatīsim funkciju , kas tiek summēts no divām citām funkcijām un var būt līdzīgs vējam:
3) 
.
1. teorēma: divu funkciju summas (mazumtirdzniecības) izmaksas līdzīgu funkciju papildu summai (mazumtirdzniecība) 
Muca: aprēķina šādas funkcijas
2. teorēma: divu funkciju darbs ir atkarīgs no formulas:
Sekas: Sliktajā zīmē var vainot pastāvīgo reizinātāju: .
Pierādījums: .
Muca
pa labi:
2) 
;
Statiskās funkcijas aprēķina pēc formulas:
Cieņa:
Formula ir derīga statiskajai funkcijai ar jebkuru soļu indikatoru. 
,
Muca: uzskaitiet šādas funkcijas:
Višnovoka: 
.
pa labi: uzskaitiet šādas funkcijas:
1)  ;
2) ;
3) ;
| 4) ; 5) ; | 6) ; 7) . |
3. teorēma: Pokhіdna privātie divi funktsіy vznachaetsya formulai:
Ilgst: ;
Muca: uzskaitiet šādas funkcijas:
2) . .
3) . 
.
pa labi: uzskaitiet šādas funkcijas:
| 1. ; 2. ; 3. ; | 4. ;
5. ;
6.  ;
| 7.  ;
8. ;
9.  .
|
8. Izpratne par locīšanas funkciju
Saliekamo funkciju diferenciācijas noteikums
Ļaujiet funkcijai piešķirt reizinātājam un funkciju reizinātājam, turklāt ar to pašu vērtību. Pēc tam bez sejas tiek piešķirta funkcija, kā to sauc locīšanas funkcija X (funkcija funkcijā).
Izmaiņas sauc par locīšanas funkcijas starpposma argumentu.
Muca:
pa labi:
- No šīm elementārajām funkcijām tiek pievienotas tsі locīšanas funkcijas:
| 1) ; 2) ; | 3)  ;
4) .
|
- No šīm elementārajām funkcijām pievienojiet locīšanas funkcijas:
| 1) , ; 2) , ; | 3) , . 4) , , . |
Višnovoka: Pokhіdna salokāmās funkcijas ї dorіvnyuє dobutka pokhіdnih elementāras funkcijas, її noliktavas. .
Muca: uzskaitiet šādas funkcijas:
- statisks, lineārs; , .
- statisks, kvadrātisks; , .
.
pa labi: uzskaitiet šādas funkcijas:
1. ;
2.  ;
| 3. ; 4. ; | 5.  ;
6. .
|
9. Pokhіdna displejs, logaritmiskās funkcijas
Muca: uzskaitiet šādas funkcijas:
1. . 
.
2. . 
.
3. . 
.
Muca: uzskaitiet šādas funkcijas:
1. . 
.
2. . 
.
pa labi: Aprēķiniet šādas funkcijas:
| 1. ; 2. ; 3. ; | 4. ; 5. ; 6. ; | 7. ; 8. . |
10. Līdzīgas trigonometriskās funkcijas
Citas apgrieztās trigonometriskās funkcijas
.
Muca: uzskaitiet šādas funkcijas:
1. 
. .
2. . .
vadītājs
. 
.
vadītājs: aprēķina šādas funkcijas.
.
pa labi: aprēķina šādas funkcijas.
Citas apgrieztās trigonometriskās funkcijas
 ;
 ;
|  ;
 .
|
pa labi: uzskaitiet šādas funkcijas:
1.
2. 
3.
4.  | 5.
6.
7.
8.
9.  | 10. 
11.
12.
13.  |
11. 
Līdzīgas funkcijas ģeometriskā sajūta
Apskatīsim funkciju.
Paņemiet fiksētu punktu funkcijas grafikā tas ir diezgan labs punkts . Mēs vadīsim sichnu . Kā punkts M tuvu punktam M 0 aiz funkcijas grafika, tad M 0 M kad palielināsit punktu, jūs ieņemsiet dažādas pozīcijas M ar punktu M 0 sіchna aizdevuma robežpozīcija M 0 T vai nu taisni M 0 T būt punkts M 0 .
Pieraksts: pārbaudiet funkcijas grafiku punktā M 0 sauc par robežnometni M 0 T steigā īstajā punktā M aiz grafika līdz punktam M0.
b- kut slikti sіyuchoї M 0 M
a-kut nahily dotichnoї M 0 T uz pozitīvu taisnu līniju uz abscisu ass.
Sihno griezuma koeficients M 0 M .
Nogriešanas koeficients M 0 T .
Skaidri taisna piegriezuma triks M 0 MA
(
). Taisna griezuma trikotāžas asā griezuma tangenss ir vairāk attīstīts kājas izvirzījumā uz blakus esošo: 
Tobto 
. Un tas nozīmē 
.
Ievērojami līdzīgas funkcijas punktos x 0
: 
.
, , otzhe, 
.
Višnovoka: Līdzīgas funkcijas ģeometrisko jēgu nosaka fakts, ka līdzīga funkcija ir līdzīga ar senāku kulta koeficientu, kas veikts funkcijas grafikam punktos ar abscisu.
Muca:
1. Atrodiet punkta kulminācijas koeficientu, kas izpildīts funkcijas grafikā punktos 
.
; 
; ; ; ; .
Ieteikums: ; ; .
2. Zināt slimā punkta griezumu, kas veikts līdz funkcijas grafikam punktā ar abscisu.
; 
; ; ; .
paralēli taisnai līnijai;
Ieliksim nepieciešamo ekstrēmuma pamatojumu.
Fermā teorēma: Šis ir iekšējais punkts x 0 no nepārtrauktas funkcijas iecelšanas apgabala - galējības punkts un šajā punktā tas ir līdzīgs, tas nav vienāds ar nulli.
Cieņa: Tomēr līdzīgas funkcijas nulles vienādība punktā x 0 joprojām nedod tiesības uz stverjuvati x 0 – funkcijas galējais punkts.
II semestris
- Augšanas un funkciju maiņas pazīmes. Lagranža teorēma.
Izraudzītā augšanas funkcija.
Funkcija y = f(x) pieaug uz intervāla X, tāpat kā jebkuram i 
nerіvnіst vykonuetsya. Citiem vārdiem sakot, lielāku argumenta vērtību piešķir funkcijas lielāka vērtība.
Izraudzītā sabrukšanas funkcija.
Funkcija y = f(x) mainās intervālā X, tāpat kā jebkuram i 
nerіvnіst vykonuetsya. Citādi, šķiet, lielāku argumenta vērtību dod mazākā funkcijas vērtība.
Lagranža teorēma: Paātrinājums ar ģeometrisko zmіst pokhіdnoї, lai sniegtu naivu skaidrojumu par derīgumu tam, kas patiešām ir dots grafikam f punktā ar intervāla abscisu (а; b), paralēli sіchnіy, kas iet garām caur punktiem A (a; f (a)), (b; f (b)).
Varam aplūkot taisni l, kas ir paralēla AB, un nav spožu punktu no grafa daļas, kas parāda atstarpi [a; b]. Mēs virzāmies taisni uz priekšu l y taisni uz priekšu līdz grafikam f tā, lai tas paliktu paralēli AB. l 0 tsієї taisnes pozīcija tiek fiksēta tajā brīdī, ja tajā ir karstie punkti ar grafika tsієyu daļu.
No 1. att. redzams, ka šādu “pirmo” dziļo punktu āda ir vērpes taisnes l 0 punkts ar grafiku f. Ievērojami abscisu qiєї punkti caur c. Tad f’(c)=tg α, de α - nogriež starp taisni l 0 un visu abscisu. Ale l || AB, tam kut α dorovnyu kutu nahil sichno AB, tobto. Tā kā funkcija ir diferencēta, tad uz intervāla (a; b) ir tāds punkts c∈ (a; b) (2. att.), ka 
- Pietiekami pazīmes, kas liecina par funkciju izmaiņām. Yakscho f'(x)< 0 в каждой точке интервала I, то функция f убывает на I.
Pietiekamas augšanas un funkciju maiņas pazīmes:
- ja funkcija f(x) ādas punkta intervālā (a, b) var būt pozitīvi dilstoša, tad pati funkcija šajā intervālā aug;
- Ja funkcija f(x) ādas punkta intervālā (a,b) var tikt negatīvi ietekmēta, tad funkcija mainās šajā intervālā.
Pieraksts. Funkcijai y \u003d f (x) var būt ekstremitāte (maksimums vai minimums) punktā x \u003d x 0, pat ja f (x 0) ir lielākā vai mazākā funkcijas vērtība reālajā apgabalā. jēga.
- Ekstrēmas funkcijas. Dosledzhennya funkcijas ekstremitāšu uz 1 soli.
Funkciju y \u003d f (x) sauc par augšanu (samazināšanos) noteiktā intervālā, pat ja x 1< x 2 выполняется неравенство f(x 1) < f (x 2) (f(x 1) >f(x2)).
Ja funkcija, kas diferencē, y = f(x) palielinās (mainās), tad tā ir līdzīga tai atzarai f ¢(x) > 0 (f ¢(x)< 0).
Punktu x 0 sauc par funkcijas f(x) lokālā maksimuma (minimuma) punktu, jo ap punktu x 0 visiem punktiem ir zināms, ka nevienmērība f(x) £ f(x 0) (f (x) ³ f(x 0) ).
Maksimālos un minimālos punktus sauc par galējībām, un funkcijas vērtības šajos punktos sauc par ekstremitātēm.
Nepieciešams prātā galējība. Tāpat punkts xo ir funkcijas f(x) galējības punkts, pretējā gadījumā f ¢(x 0) = 0, pretējā gadījumā f ¢(x 0) nevar būt. Šādus punktus sauc par kritiskiem, un tiek piešķirta pati funkcija kritiskajā punktā. Ekstrēma funkcijas blakus її kritisko punktu vidum.
Pirmajā pēdējā dienā:
Pieņemsim, ka x 0 ir kritiskais punkts. Ja f ¢ (x) pid stunda, kas iet caur punktu x 0, maina plusa zīmi uz mīnusu, tad funkcijai x 0 ir maksimums, pretējā gadījumā - minimums. Tiklīdz pāreja caur kritisko punktu nemaina zīmi, tad punkts x 0 nav ekstremāls.
Nepieciešams prātā galējība. Tāpat punkts x 0 ir funkcijas f(x) ekstrēma punkts vai f ¢(x 0) = 0, pretējā gadījumā f ¢(x 0) nevar. Šādus punktus sauc par kritiskiem, un tiek piešķirta pati funkcija kritiskajā punktā. Ekstrēma funkcijas blakus її kritisko punktu vidum.
- Funkcijas grafika izliekums. Līkuma punkti.
Funkcijas izliekums, lēciena punkti
Akordu, kas savieno punktus M 1 (x 1 f (x 1)), M 2 (x 2 f (x 2)) funkcijas f (x) grafiku dod funkcija
y \u003d L (x, x 1, x 2) \u003d f (x 1) + f (x 2) (*)
Tse perevіryaєtsya aizstāšana koordinātas x 1 x 2 labajā daļā.
Pieraksts. Funkciju f(x) sauc par izliekumu uz augšu, tātad x 1 L(x, x 1 , x 2) = f(x 1) Tā kā f ir nepārtraukts uz , dvіchі ir diferencēts (a,b) un f¢¢(x)>0 uz (a,b), tad f ir drapēts uz leju. Pierādījums. "a £ x 1 Pieraksts. Punktu x 0 sauc par funkcijas f locījuma punktu, tātad punktā x 0 tas ir absolūti punktēts un grafa punkta x 0 tuvumā atrodas gar punkta malām. Lielāko funkcijas vērtību uz ķīļa sauc par otra ķīļa lielāko vērtību, bet zemāko - par mazāko no visām trim vērtībām. Apskatīsim funkciju y=f(x) bez pārtraukuma. Kā redzat, šāda funkcija sasniedz savu augstāko un zemāko vērtību vai nu uz robežas, vai vidū. Kas attiecas uz funkcijas lielāko un mazāko vērtību, to var sasniegt atvēruma iekšējā punktā, un vērtība ir funkcijas maksimālā un minimālā vērtība, ko var sasniegt kritiskajos punktos. Šajā rangā tiek ņemts vērā lielākās un mazākās funkcijas vērtības noteikums uz vdrіzka: 1. Zināt visus funkcijas kritiskos punktus intervālā (a, b) un aprēķināt funkcijas vērtības šajos punktos. 2. Aprēķiniet funkcijas vērtību punktu līnijās x = a, x = b. 3.Z utіh otrimanih znachenih izvēlēties visvairāk un vismazāk. 1 a. Zināt ODZ un funkcijas attīstības punktus. b) Atrodiet funkcijas grafika pārtraukuma punktus ar koordinātu asīm. 2. Veikt sekošanas funkciju papildu pirmajam solim, lai zinātu funkcijas galējības punktus un augšanas un sabrukšanas intervālu. 3. Sekojiet funkcijai papildu līdzīgai citai secībai, lai zinātu funkcijas grafika lēciena punktus un tās pietūkuma un līknes intervālus. 4. Zināt funkcijas grafika asimptotiku: a) vertikāli, b) lejup. 5. Pamatojoties uz veikto pēcpārbaudi, izveidojiet funkcijas grafiku. Pieraksts. Funkciju F (x) sauc par funkcijas f (x) pirmo rindu noteiktam intervālam, tāpat kā jebkuram x no noteiktā intervāla F "(x) \u003d f (x). Muca: 1.3'yasuvati, chi є funkcija F (x) \u003d x 3 - 3x + 1 ir galvenā funkcijai f (x) \u003d 3 (x 2 - 1). Risinājums: F "(x) \u003d (x 3 - 3x + 1) \u003d 3x 2 - 3 \u003d 3 (x 2 - 1) \u003d f (x), tad F "(x) \u003d f (x) ), arī F(x) ir funkcijas f(x) pirmā rinda. Bezpersonisku primāro funkciju f(x) sauc par nenozīmīgu integrāli kā funkciju un apzīmē ar simbolu . Kā mēs to redzam no pagātnes, jo F(x) ir pirmā funkcija f(x), tad Nedefinēta integrāļa dominēšana bez vidusceļa ir tāda pati: Uzklājiet plakanas figūras Žagalnes taisne
Vairāk taisnu līniju plaknē Dekarta koordinātēs: de A, B un C ir diezgan nemainīgas, turklāt konstante A un B vienā naktī nesasniedz nulli. Vektoru ar koordinātām (A,B) sauc par normālu vektoru un perpendikulāri taisnei. Vektoru ar koordinātām (-B,A) vai (B,-A) sauc par tiešo vektoru. Taisnas līnijas izlīdzināšana, kas iet caur diviem dotiem punktiem, kas nesakrīt
Taisnas līnijas izlīdzināšana, lai tā iet cauri diviem dotiem atšķirīgiem punktiem i Parametriskās taisnes.
Taisnas līnijas parametru izlīdzināšanu var reģistrēt šādi: Kanoniski taisnas līnijas
Kanoniskais līdzinājums tiek iegūts no parametriskajiem līdzinājumiem ar vienu līdzinājumu otrā pusē: De - taisnes tiešā vektora X un Y koordinātas, tas ir, tā punkta koordinātas, kas atrodas uz taisnes. Zagalne Rivnyannia
Axe + By + C (> 0).
Vektors = (A; B) ir taisnu līniju normāls vektors. Privātie vipadki: 1) Ar + C = 0 ir taisne, kas ir paralēla Ox asij; 2) Ax + C = 0 – taisne, kas paralēla asij Oy; 3) Ax + By = 0 - iet taisni caur koordinātu vālīti; 4) y = 0 – visi Vērsis; 5) x = 0 – visi Oy. Umova taisnes paralēlisms: k1 = k2. Līniju Umov perpendikularitāte: k1 k2 = −1. Kutom starp taisnm lnijm, kas savijas, uz plakanas sauc par pasaules mazko kutvu grdu, ko veido, kad taisnes ir savijas. Kut mіzh zbіgayutsya vai paralēlas līnijas vvazhєtsya vienāda ar nulli. Izgriezt α starp divām taisnēm, kas noteiktas ar vienādiem: y=k1x+b1 (pirmā ir taisna) un y=k2x+b2 (otra ir taisna), var veikt aprēķinus pēc formulas (griezums iet no 1. taisna līnija uz 2. anti-Godiņņikova bultu): iedegums(α)=(k2-k1)/(1+k1k2) Teorēma. Ja tas ir taisns, ja tas neatrodas šajā plaknē, ja tas ir paralēls taisnei, ja tas atrodas šajā plaknē, tad tas ir paralēls pašai plaknei. a) gulēt taisni pie dzīvokļa; b) taisnei var būt tikai viens spilgts punkts; c) taisnei un plaknei nav viens un tas pats centrālais punkts. Pieraksts. Divas plaknes sauc par paralēlām, jo smaka nevar veidot miega punktus. Plakņu un paralēlisms ir norādīts šādi: | . Apskatīsim divu plakņu paralēlisma zīmi. Teorēma. Ja divas vienas plaknes taisnas plaknes, kas pārklājas, šķiet paralēlas pārējām divām taisnajām plaknēm, tad šīs plaknes ir paralēlas. Paralēlo plakņu dominēšana: Vіrіzki paralēlas taisnas līnijas, kas atrodas starp paralēlām plaknēm, rіvnі. Taisnes līnijas un plaknes paralēlisma pazīmes: 1) Tikpat taisni kā gulēt plakanā stāvoklī, būt paralēli, lai būtu taisni, kā atrasties šajā plaknē, tā ir paralēla šai plaknei. 2) Ja taisne un plakne ir perpendikulāras vienai un tai pašai taisnei, tad smaka ir paralēla. Paralēlu plakņu zīmes: 1) Kā divas taisnes, kas pārklājas, viena plakne ir paralēla divām krustojošām citas plaknes taisnēm, tad šīs plaknes ir paralēlas. 2) Ja divas plaknes ir perpendikulāras vienai, bet otra ir taisna, tad tās ir paralēlas. Taisnes un plaknes perpendikulitātes pazīmes: 1) Ja taisne ir perpendikulāra divām taisnēm, kas savijas, atrodas plaknes tuvumā, tad viena ir perpendikulāra šai plaknei. 2) Ja plakne ir perpendikulāra vienai no paralēlajām taisnēm, tad tā ir perpendikulāra otrai. Pokhila uz dzīvokli. Taisnu līniju, kas šķērso plakni un nav tai perpendikulāra, sauc par plaknes trauslumu. Teorēma par trim perpendikuliem. Taisnā līnija, kas atrodas plaknes tuvumā un ir perpendikulāra trauslākā projekcijai līdz plaknes centram, ir perpendikulāra trauslākajai līnijai. Taisnu līniju paralēlisma pazīmes kosmosa tuvumā: 1) Ja divas taisnes ir perpendikulāras vienai un tai pašai plaknei, tad tās ir paralēlas. 2) Ja vienā no plaknēm, kas pārklājas, atrodas taisni, paralēli otrai plaknei, tad tā ir paralēla plakņu taisnei. Plakņu perpendikulitātes pazīmes: ja plakne iet caur taisni, kas ir perpendikulāra otrai plaknei, tad plakne ir perpendikulāra. Teorēma par šķērsenisko perpendikulu līdz diviem šķērso līniju. Lai būtu divas taisnas līnijas, kas šķērso viena otru, ir viens šķērsvirziena perpendikuls. TEORĒMA PAR TRĪM PERpendIKULĀRĀM. Ja tas ir taisns, zīmēts uz plaknes caur slimā pamatni, perpendikulāri її projekcijai, tad tas ir perpendikulārs slimīgajam. І aizmugure: Kā taisne plaknē ir perpendikulāra slimajam, otra ir perpendikulāra slimā projekcijai. Figūru sauc par divpusēju kut, tā ir pārklāta ar diviem plakaniem plakaniem no taisnas līnijas, kas tos ieskauj. Plakanās virsmas sauc par sejām, un taisnā līnija, kas tās ieskauj, ir abpusēja kut berze. PLAKŠŅU PEPERENDIKULARITĀTES zīme. Ja plakne iet caur taisni, kas ir perpendikulāra otrai plaknei, tad plakne ir perpendikulāra. Prizma ir bagatoedrs, kura divas skaldnes ir kongruentas (vienādas) bagatokutniks, kas atrodas tuvu paralēlām plaknēm, pārējās skaldnes ir paralelogrammas un var būt paralēlas šo statīvu sānu malai. Skatīt prizmas: Taisna prizma ir prizma, kurā visas sānu ribas ir perpendikulāras pamatnei, pretējā gadījumā prizmu sauc par trauslumu. Taisnas prizmas sānu virsmas kvadrāts ir dārgāks, lai pievienotu pamatnes perimetru sānu ribas apakšai (vai augstumam). Taisnai prizmai ir ribas ar augstumu. Trauslās prizmas sānu virsmas laukums ir vienāds ar perimetra pieskaitīšanu, kas ir perpendikulāra griezumam sānu ribas apakšā. Obsyag pohiloї prizmi dorіvnyuє dobutku apgabals perpendikulāri griezumam uz ribas. Prizma ir pareiza - prizmas pamatā ir pareizais bagatokutnik, un ribas ir perpendikulāras pamatnes plaknēm. Nomainiet pareizās prizmas ar pareizajām bagatokutnikām. Bichni skaldnes ar regulāru prizmu un vienādiem taisnstūriem. Labās prizmas Bichni ribas ir vienādas. Pareizā prizma ir taisna. Prizma ir pareiza, bіchnі vіchnі іkої є є kvadrāti (augstums iаkoї dorіvnyuє rіvnієє rіvnіє іnі karvnіm pprіііvnim.prіііmіvm. Prizmas sānu virsmas laukums de P ir perpendikula perimetrs pret pārgriezumu, l ir sānu ribas garums. Nošķelto piramīdu sauc par bagatoedru, kurā pamatnes virsotnes kalpo kā virsotnes, un virsotnes sagriež pamatnei paralēla plakne. Prizma: V = S bāzes H Taisnstūra paralēlskaldņa tilpumu palielina, augstumam pievienojot pamatnes laukumu: V = SH = abc Piramīdas tilpums ir vienāds ar vienu trešdaļu no pamatnes laukuma izveidošanas augstumā: de S ir pamatnes laukums, H ir piramīdas augstums. V nošķeltās piramīdas tilpumu var uzzināt pēc formulas de H - nošķeltās piramīdas augstums, S1 un S2 - pamatu laukums. Cilindrs (sengrieķu κύλινδρος - veltnis, kovzanka) ir ģeometrisks ķermenis, ko ieskauj cilindriska virsma un divas paralēlas plaknes, kuras її peretinayut. Cilindriskā virsma - virsma, kas tiek pieņemta ar tādu taisnas līnijas kustību uz priekšu (konsolidējot) telpā, kurā ir redzams, ka stingrais punkts sabrūk plakanā līknē (tieši). Cilindra peretīns ar plakni, kas ir paralēla asij un attēlo taisnstūri. Aksiālo peretīnu sauc par perimetru, kam jāiziet cauri visam cilindram. Kvadrātveida virsmas laukums cilindram ir dārgāk pārtaisīt pamatnes pamatni uz augstuma: S=2π rh Pilna virsmas laukums cilindrs: Retin cilindrs. Konuss ir ķermenis, kas ir ierobežots ar visām izmaiņām, kas rodas no viena punkta (konusa augšdaļas) un iziet cauri plakanai virsmai. Konusa laukums: Nošķelto konusu sauc par aptinuma korpusu, taisnstūra trapeces sānu malu aptīšanu, kas ir perpendikulāra pamatnēm, sauc par nošķelto konusu. Nogrieztā konusa virsmas laukums: S=π(r12+(r1+ r2) l+ r22) Kulya - visu ieskauj kartera virsma. Sfēra (grieķu σφαῖρα - kulya) - slēgta virsma, ģeometriski izvietots punkts telpā, vienādos attālumos no dotā punkta, ko sauc par sfēras centru. Sfēras laukums: Sfēriskā sektora virsmas sfēriskās daļas laukums: , de H - segmenta augstums. Cilindrs (sengrieķu κύλινδρος - veltnis, kovzanka) ir ģeometrisks ķermenis, ko ieskauj cilindriska virsma un divas paralēlas plaknes, kuras її peretinayut. Konuss: saīsinošs konuss: V=1/3π h(r 2 +r 1 r 2 +r 2 2) Nocirsts konuss (1.20. att.) Vēsā segmenta apjoms: Vēsā sektora apjoms: Jauda: · Paralēlskaldnis ir simetrisks ap yogo diagonāles vidu. · Be-yaky vіdrіzok zintsami, scho gulēt uz paralēlskaldņa virsmas un iziet cauri yogo diagonāles vidum, sadaliet to navpіl; zokrema, visas paralēlskaldņa diagonāles vienā punktā ir notonētas un sadalītas ar to navpіl. · Paralēlskaldņa paplašinātās skaldnes ir paralēlas un vienādas. · Taisnstūra paralēlskaldņa dozhini diagonāles kvadrāts ir vienāds ar trīs jogo vimirjuvanu kvadrātu summu. Par znakhodzhennya līdzīgas trigonometriskās funkcijas
vajag čīkstēt līdzīga tabula, Un pati pokhіdnimi 6-13. Kad vajag līdzīgas vienkāršas trigonometriskās funkcijas
lai saglabātu plašu piedošanu, cienītu nākamos mirkļus: piemērs 1. Zināt saistītās funkcijas Risinājums. Teiksim s līdzīgs kosinuss viss bija prātīgi, bagātīgi teikt kādam, kurš sāk vivchati pokhіdnі. Jaku laupījums sinusa divpadsmit, dalīts ar pi? Vidpovid: vvazhat vienāds ar nulli! Šeit sinuss (funkcija!) ir pasta, jo argumentu nemaina ar ix, vai arī tas tiek mainīts, bet gan vienkārši skaitlis. Tobto, šī skaitļa sinuss ir tāds pats skaitlis. Un skaitļi (konstantes) ir pokhіdna, kā redzams no pokhіdnyh tabulām, kas ir vienādas ar nulli. Otzhe, zalishaєmo tikai mīnus sine iksa es zinu yogo pokhіdnu, neaizmirstot par zīmi: dibens 2. Zināt saistītās funkcijas Risinājums. Otrs dodanoks ir tieši tas, kurš ir pirmais dodanoks pie priekšējās dibena. Tas ir skaitlis, bet līdzīgs skaitlis ir tuvāks nullei. Mēs zinām, ka es pazaudēšu vēl vienu dodanku tāpat kā privāto: 3. piemērs. Zināt saistītās funkcijas Risinājums. Tas ir svarīgāk: šeit pirmajam dodānam nav ne arcsīna, ne citas trigonometriskas funkcijas, bet arī x funkcija. Arī diferencēšana kā papildinājums funkciju summai: Šeit jums ir vajadzīgi daži iesācēji diyah ar daļskaitļiem, Un tajā pašā laikā - šāviena trīskāršās virsmas likvidācijā. 4. piemērs. Zināt saistītās funkcijas Risinājums. Šeit burts "fi" spēlē to pašu lomu, ko "ix" priekšējās nogāzēs (un galvenokārt citās, bet ne visās) - neatkarīgas izmaiņas. Ja es pazemīgi veidoju funkcijas, es nevaru steigties apdullināt, kas vienāds ar nulli, piemēram, "fi". Tēvs: Ale, par kuru lēmums nebeidzas. Tā kā divām rokām ir šādas ekstremitātes, mums joprojām ir jāpārtaisa (atvainojiet) viraz. Tāpēc mēs pavairojam viņu reizinātāju vainas lokus, un tad dodam dodanki uz guļošajiem reklāmkarogiem un uzvaram pārējās elementārās pārvērtības: 5. piemērs. Zināt saistītās funkcijas Risinājums. Mēs zinām, ka ir tāda trigonometriskā funkcija - secant - un її formulas caur kosinusu. Atšķirībā: 6. piemērs. Zināt saistītās funkcijas Risinājums. Katram no mums ir jāatceras underwire kut formula skolas kursam. Als, aizmugure, atšķirīgi: (tse i є podvyy kuta formula)
de C - diezgan ātri. Funkciju f(x) parasti sauc par pintegrālo funkciju, un funkciju f(x) dx sauc par pintegrālo virāzi.
Tā kā f(x) ir nepārtraukts un pozitīvs, integrālis ir līknes trapeces laukums, ko ieskauj līnijas y = 0, x = a, x = b, y = f(x).
bet pie bēdīgi slavenā skatiena
kur t ir pēdējais parametrs, ax, ay ir taisnes tiešā vektora koordinātas x un y, ar kuru
; 
Taisnu līniju un plakņu savstarpējās izplešanās variācijas:
Ja divas paralēlas plaknes ir savītas ar trešo, tad to peretīnas līnijas ir paralēlas.
Piramīda (іn.-grieķu πυραμίς, рід. п. πυραμίδος) ir bagatoedrs, kura pamats ir bagatokutņiks, bet pārējās sejas ir trikutņiki, kas veido smailes virsotni.
Paralepiped (grieķu valodā παράλλος - paralēla un grieķu επιπεδον - plakana) - prizma, kuras pamatā ir kalpot par paralelogramu, jeb (līdzīgi) bagatoedrs, kuram ir sešas skaldnes un ādas paralelograms.
.
.
.
.
,
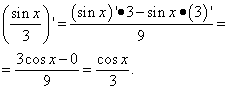
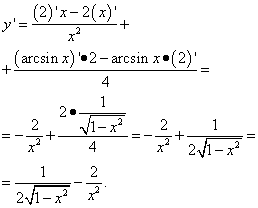
