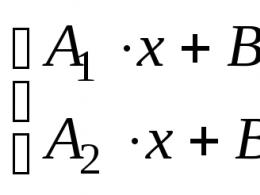Punkta projekcija uz taisnes Punkta projekcijas uz taisnes koordinātes. Punkta projekcija uz taisnes, punkta projekcijas koordinātes uz taisnes Projicēt punktu uz taisnes x y z

1-12. Punkta projekcija plaknē un taisnē

PROBLĒMAS APZINĀJUMS. Atrodiet punkta P(^PiURCHzp) projekcijas P" koordinātas plaknē Ax + By -\- Cz-\- D \u003d O,

ATŠĶIRĪBU PLĀNS. Punkta Р projekcija Р uz plaknes є substavoy perpendikulāra, nolaista no punkta Р uz q plaknes.

1. Taisnes locīšana, lai izietu caur punktu P perpendikulāri dotajai plaknei. Kuram tiešajam vektoram ņemam apgabala normālo vektoru: a = n = (A, B, C). Var izskatīties tādas pašas kanoniskas taisnas līnijas

X = At-\-xp, y = Bt-\-yp, Z=z Ct-\-Zp.

3. Plaknes līmenī aizstājot x ^ y ^ z un mainot t garumu, ir zināma parametra t = to vērtība, ar kuru tiek ņemta vērā taisnes līnija.

4. Atrastas vērtības, kas attēlojamas taisnes parametriskajā izlīdzināšanā un obsesīvi jokojot ar punkta koordinātām R".

CIEŅA. Līdzīgi tiek atrisināta problēma par punkta projekcijas koordinātu uzzināšanu uz taisnes.

BUTT. Zināt punkta Р(1,2,-1) projekcijas Р koordinātas plaknē ЗЖ - 2/4-22: - 4 = 0.

1. Taisnes locīšana, lai izietu caur punktu P perpendikulāri dotajai plaknei. Kuram tiešajam vektoram tiek uzskatīts apgabala normāls vektors: a = n =

3. Aizvietojot q virazi ar x ^ y un z līdz plaknes līmenim, ir zināma parametra ^ vērtība, kurā punktā līnija ir taisna un tiek ņemta plakne:

3 (3t + 1) - l (-t + 2) + 2 (2t - 1) - 27 = O => līdz = 2.

4. Tiešās zināmās vērtības parametrisko izlīdzināšanu aizstājot ar = 2, var ņemt zho = 7, yo = O, ^o = 1.

Tādā veidā plaknes i taisnes krustpunkts ir punkta P projekcija uz koordinātu (7,0,1) plakni.

Vidpovid. Projekcijai P ir koordinātes (7,0,1).

Vidpovidi. 1.(2,3/2,2). 2. (-3/2,-3/2,-1/2). 3. (2,-1/2,-3/2). 4. (-1/2,1,1). 5. (1,-1/2,-1/2). 6. (3/2,-1/2,0). 7. (1/2,-1,-1/2). 8. (1/2,-1/2,1/2). 9. (1/2,-1/2,1/2). 10. (1,1 / 2,0).

1.13. Taisnu līniju vai plakņu simetrija

PROBLĒMAS APZINĀJUMS. Atrodiet punkta Q koordinātas, simetriskas

ATŠĶIRĪBU PLĀNS. Shukana punkts Q atrodas uz taisnes, kas ir perpendikulārs dotajai līnijai un krustojas її punktā Р.

її projekcijas Р" uz qi taisnes.

1. Mēs zinām raibumu projekciju R dots taisni, tobto. punkts P "(1.12. iedalīšanas uzdevums). Kam:

a) varam saglabāt plaknes plakanumu, kas iet caur punktu P perpendikulāri dotajai taisnei. Parasta vektora kapacitātē plaknē var ņemt tiešo vektoru, kas dots taisnā līnijā, tas ir. n = a = (l^m^n). Pieņemams

1 (x - Xp) + m (y - UR) -f n (z - zp) \u003d 0;

b) zinām plaknes krustpunkta P "zієї koordinātes ar doto taisni. Tam rakstām taisnes izlīdzinājumu parametriskā formā

X = H-\-jo, y = mt-\-yo, Z = nt-\-ZQ.

Plaknes līmenī aizstājot x ^ y ^ z un mainot t garumu, ir zināma parametra t = to vērtība, ar kuru tiek ņemts vērā taisnes laidums;

c) vērtība to tiek atrasta taisnes parametriskajā izlīdzinājumā un ņemta no punkta P koordinātām.

2. Punkta Q koordinātas, simetriskas punktam P, ņemot vērā taisni, mēs varam mainīt domas (1). Pieņemams

XQ \u003d 2xp / - Xp, yq \u003d 2ur "- yv, ZQ \u003d 22; p / - zp.

CIEŅA. Līdzīgi problēma ir zināt punkta koordinātas, simetriskas dotas, piemēram, plaknes.

BUTT. Atrodiet punkta Q koordinātas, kas ir simetriskas punktam P(2, -1,2) gar taisni

X - 1 _ y __ Z -\-1

ATKLĀŠANA.

1. Mēs zinām raibumu projekciju R dots taisni, tobto. punkts P". Kam:

a) varam saglabāt plaknes plakanumu, kas iet caur punktu P perpendikulāri dotajai taisnei. Plaknes normālā vektora kapacitātē var ņemt dotās taisnes tiešo vektoru: n = a = (1,0,-2). Todi

Aizstājot x, y un z q virazi, plakne ir vienāda, ir zināma parametra t vērtība, tādā gadījumā tiek izvēlēta taisne un plakne: uz = -1;

c) Aizstājot zināmās vērtības taisnes parametrisko izlīdzināšanu ar = -1, ir iespējams

zhp/ = 0, g/p/ = 0, zpr = 1.

Tādā veidā plaknes i taisnes šķērspunkts ir arī punkta P projekcija uz taisnes є P”(0,0,1).

2. Punkta Q koordinātas, kas ir simetrisks punktam P, ņemot vērā taisni, tiek tālinātas (1):

XQ \u003d 2xp "- Xp \u003d -2,

VQ \u003d 2ur / - 2 / p \u003d 1,

ZQ = 2zpf – zp = 0.

Vidpovid. Krapka Q ir koordinātes (-2,1,0).

Nomazgājiet priekšnieku. Atrodiet punkta koordinātas, precīzi noteiktas taisnes simetrisko punktu P.

Šajos statūtos aizmugurē ir dota noteikta punkta projekcija uz taisnes (kopumā) un uzzīmēti mazie, ko es paskaidrošu. Tie deva iespēju noteikt punkta projekcijas koordinātas uz taisnes pie taisnstūra koordinātu sistēmas ieviešanas plaknē un triviālajā telpā, parādot pieteikumu risinājumu ar atskaites skaidrojumiem.

Navigācija sānos.

Punkta projekcija uz taisnes ir projekcija.

Visu ģeometrisko figūru šķembas sastāv no punktiem, un figūras projekcija ir visu figūras punktu bezsejas projekcija, tad figūras projekcija uz taisnes ir nepieciešama, lai projicētu figūras punktus uz taisnes līnija.

Ko sauc par punkta projekciju uz taisnes?

Pieraksts.

Punkta projekcija uz taisnes- Tse vai pats punkts, kā tas atrodas uz dotās taisnes, vai perpendikula pamats, kas nomests no punkta centra uz dotās taisnes.

Punkts H 1 ir punkta M 1 projekcija uz taisnes a, un punkts M 2 ir paša punkta M 2 projekcija uz taisnes a pret to, ka M 2 atrodas uz taisnes a.

Punkta projekcijas apzīmējums uz taisnes ir gluži kā slīpums plaknē, tātad slīpums triviālā telpā.

Plaknē, lai ierosinātu punkta M 1 projekciju uz taisnes a, ir jānovelk taisne b, lai izietu caur punktu M 1 i ir perpendikulāra taisnei a. Tad taisnes a i є šķērspunkts ir punkta M 1 projekcija uz taisnes a.

Triviālā telpā punkta M 1 projekcija uz taisnes a ir taisnes a šķērslīnijas punkts un plakne, kas iet caur punktu M 1 perpendikulāri taisnei a.

Punkta projekcijas uz taisnes koordinātu vērtība - teorija un pielietojums.

Ir svarīgi zināt punkta projekcijas koordinātas uz taisnes, ja punkts, kas tiek projicēts, ir tiešs uzdevums taisnstūra Oxy koordinātu sistēmā plaknē. Pēdējā lieta, kas jāparāda, ir, kā uzzināt punkta projekcijas koordinātas taisnā taisnstūra koordinātu sistēmā Oxyz triviālā telpā.

Punkta projekcijas koordinātas tieši plaknē.

Uz plaknes ir fiksēts Oxy, dots punkts uz taisnes a, un jāpiešķir punkta M 1 projekcijas koordinātas uz taisnes a.

Atraisīsim pasūtījumu.

Mēs velkam caur punktu M 1 taisni b, perpendikulāri taisnei a, i, taisnu līniju krustošanās punkts a і b jaka H 1 ir nozīmīgs. Todi H1 ir punkta M1 projekcija uz taisnes a.

Z veica ātri un loģiski algoritms, kas ļauj uzzināt punkta projekcijas koordinātas uz taisnes a:

Apskatīsim punkta projekcijas koordinātas uz taisnes, kas atrodas dibena augšdaļā.

dibens.

Taisnstūra koordinātu sistēmas Oxy plaknē dotais punkts ir taisne a , kas ir taisne

Risinājums.

Rivnyannya taisne mums ir skaidra, tāpēc mēs varam pāriet uz citu algoritmu.

Mēs ņemam taisnes b izlīdzināšanu tā, lai izietu caur punktu M1 i ir perpendikulāra taisnei a. Tam mums vajadzīgas taisnes b tiešā vektora koordinātas. Tā kā taisne b ir perpendikulāra taisnei a, tad taisnes a normālvektors ir taisnes b tiešais vektors. Acīmredzot normāls līniju vektors є vektors ar koordinātām , arī tiešs taisnes vektors є vektors . Tagad mēs varam uzrakstīt taisnes b kanonisko izlīdzinājumu, mēs zinām punkta koordinātas, uz kuru pusi jāiet, un tiešā vektora koordinātas: .

Zaudēja zināt taisnes a і b krustpunkta koordinātas, yaki dod punkta M 1 projekcijas koordinātas uz taisnes a. Pirmajā pusē pāriesim no taisnās līnijas kanoniskajām līnijām uz її zagalny līniju: . Tagad izveidosim izlīdzinājumu sistēmu no taisnu līniju a un b augšējiem izlīdzinājumiem, pēc kuriem mēs zinām її rozvyazannya (ja nepieciešams, dodieties uz rakstu):

Tādā veidā punkta projekcija uz taisnes var koordinēt.

Ieteikums:

dibens.

Taisnstūra koordinātu sistēmas Oxy plaknē ir uzstādīti trīs punkti. Atrodiet punkta M1 projekcijas koordinātas uz taisnes AB.

Risinājums.

Punkta M 1 projekcijas koordinātu vērtībai uz taisnes AB to nosaka algoritms.

Uzrakstīsim taisni, kas iet caur diviem dotajiem punktiem i:
.

Tagad jūs varat iet cauri vecajai kanoniskajai taisnei AB līdz dziļajai taisnei AB un turpināt risinājumu pēc analoģijas ar priekšējo sadursmi. Apskatīsim vēl vienu taisnes b izlīdzināšanas veidu, kas ir iziet caur punktu M1 perpendikulāri taisnei AB.

No taisnes AB kanoniskā izlīdzinājuma mēs ņemam taisnes izlīdzināšanu ar griezuma koeficientu: . Taisnes AB virsotnes koeficients ir progresīvāks, un taisnes b virsotnes koeficients ir perpendikulārs taisnei AB (brīnieties par taisnu līniju garīgo perpendikulitāti). Todі vnyannya taisna līnija b, scho, lai izietu caur punktu i maє kutovy koefіtsієnt, maє vglyad.

Lai noteiktu punkta projekcijas koordinātas uz taisnes AB, tika zaudēta izlīdzinājumu sistēma. :

Ieteikums:

Sīkāk aplūkosim punkta projekcijas nozīmīgās koordinātes uz koordinātu taisnēm Ox un Oy, kā arī uz tām paralēlajām taisnēm.

Ir skaidrs, ka punkta projekcija uz koordinātu taisni Ox , kas šķiet nevienmērīgi vienāda ar redzes līniju, ir punkts ar koordinātām . Tāpat punkta projekcijai uz koordinātu līnijas Oy var būt koordinātas.

Neatkarīgi no tā, vai tas ir taisns, paralēls abscisu asij, tas var būt iestatīts uz nesaprotamu, taisnu prātu , Un taisne, kas ir paralēla ordinātu asij, ir vienāda ar prātu . Punkta projekcijas uz taisnes ir punkti ar koordinātām un ir redzami.

dibens.

Kādas koordinātes var būt punkta projekcija uz koordinātu līnijas Oy un taisnes.

Risinājums.

Punkta projekcija uz taisnes Oy ir punkts ar koordinātām.

Pārrakstīsim taisni taisni jaku. Tagad jūs varat skaidri redzēt, ka punkta projekcija var tieši koordinēt.

Ieteikums:

І.

Punkta projekcijas koordinātas uz taisnes triviālās telpas tuvumā.

Tagad pāriesim pie taisnes punkta projekcijas koordinātu vērtības, izmantojot triviālajā telpā ieviesto taisnstūra koordinātu sistēmu Oxyz.

Lai telpai ir fiksēta taisnstūra koordinātu sistēma Oxyz, dots punkts , Taisne a un ir jāzina punkta M 1 projekcijas koordinātas uz taisnes a.

Atraisīsim pasūtījumu.

Mēs ļausim plaknei iet caur punktu M1 perpendikulāri taisnei a. Punkta M 1 projekcija uz taisnes a ir taisnes un plaknes šķērslīnijas punkts. Tādā veidā mēs ņemam algoritms, kas ļauj uzzināt punkta projekcijas koordinātas taisni a:

Apskatīsim risinājumu.

dibens.

Taisnstūra koordinātu sistēmai Oxyz ir punkts un taisne a , un taisnei a tiek piešķirts taisnes kanoniskais izlīdzinājums prāta telpā . Atrodiet punkta M1 projekcijas koordinātas uz taisnes a.

Risinājums.

Punkta M 1 projekcijas koordinātu piešķiršanai uz taisnes to paātrina ar algoritmu.

Rivnjaņa prātā uzreiz aizklīda pie mums, tāpēc pāriesim pie cita krokodila.

Mēs noņemam plaknes līdzenumu, jo tā ir perpendikulāra taisnei un iet caur punktu. Tam mums jāzina apgabala normālā vektora koordinātas. Iepazīsim viņus. No taisnes a kanoniskajiem izlīdzinājumiem var redzēt tiešā vektora koordinātas pa taisni: . Taisnes tiešais vektors ir apgabala normāls vektors, kas ir perpendikulārs taisnei a. Tobto, - Normālā laukuma vektors. Todі vnyannya plakne, scho, lai izietu caur punktu i maє normāls vektors , var izskatīties .

Zaudēju zināt punkta koordinātas, taisnes a krustpunktu un plakni - smird є shukanimi koordinātas punkta projekcijas uz taisnes a. Mēs parādām divus šīs nozīmes veidus.

Pirmā metode.

No taisnes a kanoniskajiem izlīdzinājumiem mēs iegūstam divu plakņu izlīdzināšanu, kas pārklājas, it kā tās apzīmē taisnu līniju a:

Līnijas punkta koordinātas ka dzīvoklis mēs to uztveram, izstrādājot lineāro saskaņošanas sistēmu ar prātu . Zastosuyemo (ja jums ir nepieciešams vairāk vai ja ir cita metode lineāro izlīdzināšanas sistēmu atsaistīšanai, pārtrauciet to):

Šādā secībā punkts ar koordinātām ir punkta M projekcija uz taisnes a.

Vēl viens veids.

Zinot taisnes a kanonisko izlīdzināšanu, ir viegli pierakstīt taisnes parametrisko izlīdzināšanu telpā: . Aplūkosim to perspektīvā aizstāt x , y un z їх izteiksmi, izmantojot parametru:

Tagad mēs varam aprēķināt taisnes a krustpunkta koordinātas un laukumu aiz līnijas a parametriskajām līnijām:

Tsya raksts, kurā aplūkota izpratne par punkta projekciju uz taisnes (visi). Mi damo yoma tika iecelta vikoristannya mazajam, ko es paskaidroju; Vivchimo veids, kā piešķirt punkta projekcijas koordinātas uz taisnes (uz plakanas vai triviālas telpas); Izmēģināsim.

Rakstā "Punkta projicēšana plaknē, koordinātes" prātojām, vai figūras dizains ir jāsaprot ar perpendikulāra vai ortogonāla dizaina jēdzieniem.

Visas ģeometriskās figūras ir salocītas punktos; Tāpēc, lai varētu projicēt figūru uz taisnes, ir jāņem vērā iespēja projicēt punktu uz taisnes.

Tikšanās 1

Punkta projekcija uz taisnes- tas ir pats punkts, jo tam jāatrodas uz dotās taisnes, vai perpendikula pamats, kas nomests no punkta centra uz dotās taisnes.

Apskatīsim mazos zemāk: punkts H 1 kalpo kā punkta M 1 projekcija uz taisnes a, bet punkts M 2, kas atrodas uz taisnes, ir projekcija uz sevi.

Šis apzīmējums ir pareizāks vipadku virspusē un trivi- mer telpā.

Lai ņemtu punkta M 1 projekciju uz plaknes taisnes a, novelciet taisni b tā, lai tā iet caur doto punktu M 1 i ir perpendikulāra taisnei a. Šādā secībā taisnes a un b krustošanās punkts būs punkta M 1 projekcija uz taisnes a.

Trivi-pasaules telpā punkta projekcijai uz taisnes būs punkts uz taisnes a un plakne α, kas iet caur punktu M 1 un ir perpendikulāra taisnei a.

Punkta projekcijas uz taisnes koordinātu vērtība

Apskatīsim ķēdes dizaina ainavās plakanā un triviālajā plašumā.

Dodiet mums uzdevumu par taisnstūra koordinātu sistēmu O x y, punkts M1 (x1, y1) i taisne a. Ir jāzina punkta M1 projekcijas koordinātas uz taisnes a.

Caur doto punktu M 1 (x 1, y 1) izlaidīsim taisnei b perpendikulāri taisnei a. Pārtraukuma punkts ir atzīmēts kā H1. Punkts H 1 būs punkta M 1 projekcijas punkts uz taisnes a.

No apraksta ir iespējams noformulēt algoritmu, kas ļauj uzzināt punkta M 1 (x 1 y 1) projekcijas koordinātas uz taisnes a:

Taisnu līniju locīšana (kā tas nav norādīts). Par zdіysnennya ts_єї dії nebhіdna navička skladannya galvenā rivnyan uz dzīvokli;

Reģistrē taisnes b izlīdzināšanu (lai izietu caur punktu M 1 un perpendikulāri taisnei a). Šeit tiks papildināts raksts par taisnes izlīdzināšanu, lai izietu caur doto punktu perpendikulāri dotajai taisnei;

Ir skaidrs, ka projekcijas koordinātas tiek ņemtas par taisnes a un b krustpunkta koordinātas. Un tam ir pierādīta vienādību sistēma, piemēram, noliktavas - taisnu a un b izlīdzināšana.

dibens 1

Plaknē O x y dotais punkts M 1 (1, 0) ir taisne a (augstāks izlīdzinājums - 3 x + y + 7 = 0). Nepieciešams norādīt punkta M1 projekcijas koordinātas uz taisnes a.

Risinājums

Tiešās līnijas dotais izlīdzinājums, ka saskaņā ar algoritmu mēs pārejam uz īsāko taisnes b līdzinājuma ierakstu. Taisne b ir perpendikulāra taisnei a, tāpēc taisnes a normālvektors kalpo kā taisnes b tiešais vektors. Tad taisnes b tiešo vektoru var uzrakstīt kā b → = (3, 1). Pierakstīsim taisnes b kanonisko izlīdzinājumu, bet mums ir jāiestata arī punkta M 1 koordinātas, lai izietu taisni b:

Pēdējais griezums parāda taisnes a un b krustpunkta koordinātas. Pārejam no kanoniskās rivnjaņas uz taisno līniju її rivnyannia:

x - 1 3 = y 1 ⇔ 1 (x - 1) = 3 y ⇔ x - 3 y - 1 = 0

Izveidosim izlīdzinājumu sistēmu no taisnes a un b augšējiem izlīdzinājumiem

3 x + y + 7 = 0 x - 3 y - 1 = 0 ⇔ y = - 3 x - 7 x - 3 y - 1 = 0 ⇔ y = - 3 x - 7 x - 3 ( - 3 x - 7 ) - 1 = 0 ⇔ ⇔ y = - 3 x - 7 x = - 2 ⇔ y = - 3 (- 2) - 7 x = - 2 ⇔ y = - 1 x = - 2

Nu, mēs atņēmām punkta M 1 (1, 0) projekcijas koordinātas uz taisnes 3 x + y + 7 = 0: (- 2 , - 1) .

Ieteikums: (- 2 , - 1) .

Atskaite tiks izskatīta, ja nepieciešams norādīt dotā punkta projekcijas koordinātas uz koordinātu taisnes un paralēlām taisnēm.

Dotās koordinātu līnijas O x і O y, kā arī punkts M 1 (x 1, y 1). Es sapratu, ka dotā punkta projekcija uz taisnes koordinātu O x formā y = 0 būs punkts ar koordinātām (x 1, 0) . Tātad i ir dotā punkta projekcija uz koordinātu taisnes O y ar koordinātām 0 , y 1 .

Ja tā ir diezgan taisna līnija, kas ir paralēla abscisu asij, varat ievietot nesalīdzināmas dziļas līnijas B y + C \u003d 0 ⇔ y \u003d - C B un taisnu līniju, kas ir paralēla y asij - A x + C \ u003d 0 ⇔ x \u003d - C A.

Tad punkta M 1 (x 1, y 1) projekcijas uz taisnes y \u003d - C B i x \u003d - C A kļūst par punktiem ar koordinātām x 1, - C B i - C A, y 1.

dibens 2

Ņemiet punkta M 1 (7, - 5) projekcijas koordinātas uz koordinātu taisnes O y , kā arī uz taisnes, kas ir paralēla taisnei O y 2 y - 3 = 0 .

Risinājums

Uzrakstīsim dotā punkta projekcijas koordinātes uz taisnes O y: (0 - 5) .

Pierakstīsim taisnes 2 y - 3 = 0 yak y = 3 2 izlīdzinājumu. Kļūst skaidrs, ka dotā punkta projekcija uz taisnes y = 3 2 ar koordinātu matricu 7 3 2 .

Ieteikums:(0 , - 5) un 7 , 3 2 .

Pieņemsim, ka triviālajai telpai ir taisnstūra koordinātu sistēma O x y z , punkts M 1 (x 1 , y 1 , z 1) un taisne a . Mēs zinām punkta M1 projekcijas koordinātas uz taisnes a.

Mēs ļausim plaknei α iziet caur punktu M 1 i, kas ir perpendikulāra taisnei a. Dotā punkta projekcija uz taisnes a kļūst par punktu uz taisnes a un plakni α. Pamatojoties uz to, mēs ieviešam algoritmu punkta M 1 (x 1, y 1, z 1) projekcijas koordinātu vērtībai uz taisnes a:

Mēs pierakstām taisnās līnijas a izlīdzināšanu (kā tas nav norādīts). Lai saprastu, kurš vadītājs, ir jāmācās no raksta par taisnu līniju izlīdzināšanu telpā;

Vai mēs varam uzglabāt plakanumu?

Mēs zinām punkta M 1 (x 1, y 1, z 1) projekcijas koordinātes uz taisnes a - būs taisnes α šķērslīnijas punkta un α plaknes koordinātes. (palīdzībai - raksts “Plaknes taisnes šķērslīnijas punkta koordinātes”).

dibens 3

Dota taisnleņķa koordinātu sistēma O x y z , i in nіy - punkts М 1 (0, 1, - 1) i taisne a . Taisne a atbilst kanoniskajam izlīdzinājumam: x + 23 = y - 6 - 4 = z + 11. Nosakiet punkta M1 projekcijas koordinātas uz taisnes a.

Risinājums

Vykoristovuёmo vkazyvshee algoritms. Rivnyannya taisna līnija, pirmais solis tiek izlaists ar algoritmu. Pierakstīsim laukuma α izlīdzinājumu. Kurām apgabala normālvektora koordinātas ir nozīmīgas. No dotajiem taisnes a kanoniskajiem izlīdzinājumiem varam redzēt taisnes tiešā vektora koordinātas: (3, - 4, 1), kas būs apgabala α normālvektors, kas ir perpendikulārs taisnei. a. Todi n → = (3, - 4, 1) ir laukuma α normālvektors. Šādā secībā α matime plakne izskatījās vienāda:

3 (x - 0) - 4 (y - 1) + 1 (z - (- 1)) = 0 ⇔ 3 x - 4 y + z + 5 = 0

Tagad mēs zinām taisnes un plaknes α krustojuma koordinātas, kurām ir divi veidi:

1. Kanoniskās izlīdzināšanas uzdevumi ļauj veikt divu plakņu izlīdzināšanu, kas pārklājas un attēlo taisnu līniju a:

x + 2 3 = y - 6 - 4 = z + 1 1 ⇔ - 4 (x + 2) = 3 (y - 6) 1 (x + 2) = 3 (z + 1) 1 ( y - 6) = - 4 (z + 1) ⇔ 4 x + 3 y - 10 = 0 x - 3 z - 1 = 0

Lai uzzinātu taisnes 4 x + 3 y - 10 = 0 x - 3 z - 1 = 0 un plaknes 3 x - 4 y + z + 5 = 0 šķērslīnijas punktus, sadalīsim izlīdzināšanas sistēma:

4 x + 3 y - 10 = 0 x - 3 z - 1 = 0 3 x - 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x - 3 z = 1 3 x - 4 y + z = - 5

Tādā veidā Krāmera metode ir uzvaroša, taču jūs varat noskaidrot, vai tā ir parocīga:

∆ = 4 3 0 1 0 - 3 3 - 4 1 = - 78 ∆ x = 10 3 0 1 0 - 3 - 5 - 4 1 = - 78 ⇒ x = ∆ x ∆ = - 78 - 78 = 1 ∆ y = 4 10 0 1 1 - 3 3 - 5 1 = - 156 ⇒ y = ∆ y ∆ = - 156 - 78 = 2 ∆ z = 4 3 10 1 0 1 3 - 4 - 5 = 0 ⇒ z = ∆ 0-78 = 0

Tādā veidā dotā punkta projekcija uz taisnes a ir punkts ar koordinātām (1, 2, 0)

1. Pamatojoties uz kanonisko izlīdzinājumu uzdevumiem, ir viegli pierakstīt taisnu līniju parametrisko izlīdzināšanu telpā:

x + 2 3 = y - 6 - 4 = z + 1 1 ⇔ x = - 2 + 3 λ y = 6 - 4 λ z = - 1 + λ

Iedomāsimies plaknes līmenī, ko var redzēt kā 3 x - 4 y + z + 5 = 0, nevis x , y і z їх izteiksmi caur parametru:

3 (- 2 + 3 λ) - 4 (6 - 4 λ) + (- 1 + λ) + 5 = 0 ⇔ 26 λ = 0 ⇔ λ = 1

Aprēķināsim taisnes a krustpunkta un plaknes α koordinātas aiz taisnes a parametriskajiem izlīdzinājumiem pie λ = 1:

x = - 2 + 3 1 y = 6 - 4 1 z = - 1 + 1 ⇔ x = 1 y = 2 z = 0

Tādējādi dotā punkta projekcijai uz taisnes a ir koordinātas (1, 2, 0)

Ieteikums: (1 , 2 , 0)

Visbeidzot, ir svarīgi, ka punkta M 1 (x 1, y 1, z 1) projekcijas uz koordinātu taisnēm O x , O y i O z būs punkti ar koordinātām (x 1 , 0 , 0) , (0 , y 1 , 0 ) un (0 , 0 , z 1) ir derīgs.

Kā atcerējāties piedošanu tekstā, esiet laipni, skatiet to un nospiediet Ctrl + Enter