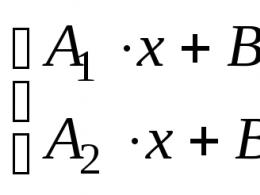Cikliskās grupas. Cikliskās apakšgrupas Elementu skaits, kas tiek ģenerēti cikliskajā grupā
Ciklisko grupu apakšgrupas
Nāk teorēma, kas definē ciklisko grupu apakšgrupas esamību.
Teorēma 1.4. Cikliskās grupas apakšgrupa ir cikliska. Jakšo G = (a)uH - grupas G nevienā apakšgrupa, moH = (un P), de p - mazākais naturālais skaitlis, piemēram, p e N.
Pierādījums. Nāc, G = (a) tas H- grupas apakšgrupa G. Kā apakšgrupa H tad vientuļš H =(f) – cikliskā grupa. Aiziet H- apakšgrupa, kas nav viena. Ievērojami cauri P mazākais naturālais skaitlis, tātad pildspalva, un dariet mums to zināmu H \u003d (a p). Iekļaušana ( a p) h H acīmredzot. Ieslēdzam to. Aiziet h un H. Oskilki G = (a), tad tas ir īsts šovs pirms, nu ko h = a k. Podilimo pirms tam uz P par daudz: pirms tam = nq+ g, de 0 lpp. g F 0, tad ņem h = a līdz = a pa p h a g, zvaigznes a r \u003d a ~ p hN e N. Sasniedza izcilību ar minimālu displeju P. Arī r = 0 i uz - nq. Zvidsi h = a k = a p h e a"). Šajā pakāpē H h ( a n), vēlāk, H = (a e). Teorēma ir pabeigta.
Cikliskās grupas elementu ģenerēšana
Kādi elementi var radīt ciklisku grupu? Ir divas progresējošas teorēmas.
Teorēma 1.5. Ļaujiet cikliskajai grupai G = (a) dot nereducētu secību. Todi (a) — (a uz) tad, un tikai tad, ja līdz - ± 1.
Pierādījums. Aiziet G = (a),|a| = ° ° i (a) = (Ak). Todі іsnuє tіla kіlkіst P, nu ko a = a kp. Zvіdsi a * "-1 \u003d e, un oskolki | a = tad kp - 1 = 0. Alethodi kp = 1 ih-± 1. Nopietna cietība ir acīmredzama.
Teorēma 1.6. Dosim ciklisku grupu G = (a) secībai m. gcd(/s, t) = 1.
Pierādījums.(=>) Nāc (a) = (pirms), dariet mums zināmu, ka GCD(/s, t) - 1. Nozīmīgi SNDC, t) – d. Oskilki a e (a)–(a līdz), tad a = a kp ar pašreizējo veselumu P. Precīzai elementu secībai zvaigznes dzied, scho (1 - kp) : t, tobto. viens - kp = mt reālam veselam skaitlim t. Ale todi 1 = (kp + mt) : d, zvaigznes d = 1 × GCD(/s, t)= 1.
(Ejam uz NID (k, t) = 1. Let's know what a) = (Ak). Paziņojums (a iepriekš) h (a) ir acīmredzams. Atpakaļ, prātā DIEVS#, t) = 1 sekojoši cipari і un v, tādi ki + mv= 1. Koristuyuchis tim sho | a | - t, pieņemams a = a ku + mv = a ku a mv = a kі e (a līdz). Oce, (a) = (a līdz). Teorēma ir pabeigta.
Uzmini kas Eilera funkcija f(t) apzīmē naturālo skaitļu skaitu, kas nemaina naturālo skaitļu t un savstarpēji vienkārši tie. Mums ir jāuzņemas sekas.
Pēdējais. Cikliskā grupa a) pasūtījums t maє f(t) dažādu elementu, kas tiek ģenerēti.
Dotajai teorēmas 1.5 ģeometriskajai precizitātei mēs attēlojam ciklisko grupu G = (a) pasūtījums t likmes punkti A 0, A b ..., A t _ b sadaliet to t vienādās daļās. elements a līdz dotās grupas, kas parāda punktus Un pirms tam radīs dažus un tikai dažus, ja secīgi punkti A 0, A līdz, A 2k utt., mēs nonāksim pie punkta A]. Uzzināsim visu pirms tam plkst t= 10 uzskaitīsim tikai vipadkіv (1.5. att.). Rezultātā mēs ņemam pirms =1,3, 7, 9. Cikliskajai grupai a) tse nozīmē, ka (a) \u003d (a 3) \u003d (a 7) \u003d (a 9). atpakaļ: zini pirms, savstarpēji vienkārši ar vienu un to pašu numuru t, jūs varat laipni vikreslyuvaty vodpovidnu "zirochka", stingri zinot, ka agri chi pizno malks ādas punktā, vairāk (a) = ( a uz).
Lai g ir G. Todi grupas papildu elements, pieņemot minimālo apakšgrupu  , ko ģenerē viens elements
, ko ģenerē viens elements  .
.
Pieraksts.
Minimālā apakšgrupa  , ko ģenerē viens G grupas elements g, sauc cikliskā apakšgrupa G grupa.
, ko ģenerē viens G grupas elements g, sauc cikliskā apakšgrupa G grupa.
Pieraksts.
Tāpat kā G grupa ir dzimusi no viena elementa, tas ir.  , tad to sauc cikliskā grupa.
, tad to sauc cikliskā grupa.
Aiziet  reizināšanas grupas G elements, tā pati minimālā apakšgrupa, ko ģenerē šis elements, tiek veidota no prātā esošā elementa
reizināšanas grupas G elements, tā pati minimālā apakšgrupa, ko ģenerē šis elements, tiek veidota no prātā esošā elementa

Apskatīsim elementa soli  , tad. elementi
, tad. elementi
 .
.
Divas iespējas:
1. Usі solis elements g raznі, tobto. 
 , tad šeit jāsaka, ka elementu g nevar samazināt secībā.
, tad šeit jāsaka, ka elementu g nevar samazināt secībā.
2. Є zbіgi soļi, tobto. , aliņš  .
.
І šeit elements g ir gala secība.
Pareizi, sakiet man, piemēram,  і
і  todi,
todi,  , tad. noteikt pozitīvus soļus
, tad. noteikt pozitīvus soļus  elements
elements  , vienāds ar vienu elementu.
, vienāds ar vienu elementu.
Ļaujiet d - vismazāk pozitīvais elementa līmeņa rādītājs  , par kuru
, par kuru  . Tad šķiet, ka stihija
. Tad šķiet, ka stihija  Maija pēdējais pasūtījums, vienāds ar d.
Maija pēdējais pasūtījums, vienāds ar d.
Višnovoka.
Ir sava veida grupa G pēdējā secībā (  ) visi elementi būs galīgajā kārtībā.
) visi elementi būs galīgajā kārtībā.
Lai g ir reizināšanas grupas G elements vai reizināšanas apakšgrupa  tiek summēts no visām dažādajām elementa g darbībām. Otzhe, elementu skaits apakšgrupā
tiek summēts no visām dažādajām elementa g darbībām. Otzhe, elementu skaits apakšgrupā  zbigaєtsya ar elementa secību
zbigaєtsya ar elementa secību  tobto.
tobto.
elementu skaits grupā  viena elementa secība
viena elementa secība  ,
,
 .
.
No otras puses, var būt tāda pati cietība.
Stingrība.
Pasūtiet  lai kāds būtu elements
lai kāds būtu elements  šī elementa ģenerētās minimālās apakšgrupas secībā
šī elementa ģenerētās minimālās apakšgrupas secībā  .
.
Pierādījums.
1.Jakšo  - Galīgā pasūtījuma elements
- Galīgā pasūtījuma elements  , tad
, tad
2. Jakšo  - Nekonsekventas kārtības elements, tad nenesiet neko.
- Nekonsekventas kārtības elements, tad nenesiet neko.
Yakscho elements  var pasūtīt
var pasūtīt  , tad šim nolūkam visi elementi
, tad šim nolūkam visi elementi

atšķiras un esi solis  zbіgaєtsya ar vienu no šiem elementiem.
zbіgaєtsya ar vienu no šiem elementiem.
Tiesa, lai ārišķīgs solis  , tad.
, tad.  - pietiekami daudz un neej
- pietiekami daudz un neej  . Tas pats numurs
. Tas pats numurs  var redzēt vienā mirklī
var redzēt vienā mirklī  , de
, de  ,
, . Todі, vikoristuuuuuuuuuuu g elementa jaudas līmenis,
. Todі, vikoristuuuuuuuuuuu g elementa jaudas līmenis,
 .
.
Zokrema, jakščo.
dibens.
Aiziet  - Ābela veselo skaitļu grupa ir aditīva. Grupu G veido no minimālas apakšgrupas, ko ģenerē viens no elementiem 1 vai –1:
- Ābela veselo skaitļu grupa ir aditīva. Grupu G veido no minimālas apakšgrupas, ko ģenerē viens no elementiem 1 vai –1:

 ,
,
otzhe,  - Bezkіnechna tsiklіchna grupa.
- Bezkіnechna tsiklіchna grupa.
Pēdējās kārtas cikliskās grupas
Tāpat kā galīgās kārtas cikliskās grupas piemērs, tas ir skaidrs grupa ietīšanas pareizo n-kutnik shodo yogo uz centru  .
.
Grupu elementi
є pagrieziet n-kutniku pret godinņikova bultu uz kuti
Grupu elementi
 є
є
 ,
,
un no ģeometriskās spoguļošanas ir skaidrs, ka

 .
.
grupai  atriebties elementiem, tobto.
atriebties elementiem, tobto.  , bet gan grupas apmierinošais elements
, bet gan grupas apmierinošais elements  є
є  , tad.
, tad.
 .
.
Aiziet  todi (dal. 1. att.)
todi (dal. 1. att.)

Rīsi. viens –
grupai  - pareizā trikutnik ABC shodo iesaiņojums uz centru O.
- pareizā trikutnik ABC shodo iesaiņojums uz centru O.
Algebriskā darbība grupā  - Pēdējais iesaiņojums pret gada bultu, uz kut, daudzkārtējs
- Pēdējais iesaiņojums pret gada bultu, uz kut, daudzkārtējs  , tad.
, tad.
Zvorotny elements  - ietīšana aiz gada bultiņas uz kut 1, tobto.
- ietīšana aiz gada bultiņas uz kut 1, tobto.
 .
.
K tabulaechi
Kincevih grupu analīzi, visticamāk, veiks ar Keli papildu tabulām, kuras ir detalizētākas “reizināšanas tabulā”.
Lai grupa G atriebjas elementiem n.
Manuprāt, galds Keli є kvadrātveida matrica ir n rindas un n rindas.
Ādas rindai un ādas slānim viens vai vairāki grupas elementi.
elements  tabula Kelі, scho stāvēt uz i-tās rindas un j-tās kolonnas tīklenes, līdz i-tā elementa "reizināšanas" operācijas rezultātam ar grupas j-to elementu.
tabula Kelі, scho stāvēt uz i-tās rindas un j-tās kolonnas tīklenes, līdz i-tā elementa "reizināšanas" operācijas rezultātam ar grupas j-to elementu.
Muca. Ļaujiet grupai G atriebt trīs elementus (g 1, g 2, g 3). Darbība "reizināšanas" grupā. Šajā brīdī Keli tabula var izskatīties:

Cieņa. Pie tabulas Keli ādas rindas un ailes ir atrasti visi grupas elementi un nav ne smakas. Tabula Keli, lai aizstātu visu informāciju par grupu. Ko jūs varat teikt par šīs grupas spēku?
1. Vienīgais šīs grupas elements ir g1.
2. Grupa ir ābeliska, jo tabula ir simetriska gar galveno diagonāli.
3. Grupas ādas elementam ir nepieciešams
par g 1 aptinums є elements g 1 par g 2 elements g 3 .
Ejam uz grupām  Šūnu tabulas.
Šūnu tabulas.

Par galveno elementu nozīmi elementam, piemēram,  , tas ir nepieciešams pēc kārtas, kas ir nepieciešams elementam
, tas ir nepieciešams pēc kārtas, kas ir nepieciešams elementam  zināt stovpets atriebības elementu
zināt stovpets atriebības elementu  . elements
. elements  vidpovіdny dots stovptsyu i є vorotnym uz elementu
vidpovіdny dots stovptsyu i є vorotnym uz elementu  , jo
, jo  .
.
Tāpat kā Keli galds ir simetrisks tāpat kā galvas diagonāle, tse to nozīmē

- Tobto. grupas darbība ir komutatīva. Argumenta labad Keli tabula ir simetriska, lai gan galvas diagonāle nozīmē, ka operācija in  komutatīva, tas ir.
komutatīva, tas ir.  ,
,
grupa  - Abelova.
- Abelova.
Var redzēt visu pareizā n - kosin simetrijas transformāciju grupu  pievienojot operācijai plašā pagrieziena papildu operācijas aptīšanu ap simetrijas asīm.
pievienojot operācijai plašā pagrieziena papildu operācijas aptīšanu ap simetrijas asīm.
Par trikutnik  , un grupa
, un grupa  atriebties sešiem elementiem
atriebties sešiem elementiem
de  Tse pagrieziens (div. mazs. 2) uz pareizo augstumu, mediānu, sadalīšanu un var izskatīties:
Tse pagrieziens (div. mazs. 2) uz pareizo augstumu, mediānu, sadalīšanu un var izskatīties:
 ;
;
 ,
,
,
 .
.


Rīsi. 2.– grupa  - Parastā trikotāžas ABC simetrijas maiņa.
- Parastā trikotāžas ABC simetrijas maiņa.
Bagato, otrimane šī procesa rezultātā, tekstā parādās kā . Izpelnīties cieņu ir tas pats, kas 0 = e.
Krājums 5.7
3 grupas G =< Z 6 , +>var buti otrimani chotiri cikliskās apakšgrupas. Tse H 1 =<{0},+>, H2 =<{0, 2, 4}, +>, H 3 =<{0, 3}, +> і H 4 \u003d G. Ar cieņu, ja darbība ir saskaitīšana, tad a n nozīmē n reizināšanu ar a. Ir arī vērts atzīmēt, ka visās šajās grupās darbība ir 6. moduļa pievienošana. Tālāk ir parādīts, kā ir zināmi šo ciklisko apakšgrupu elementi.
a. Cikliskā apakšgrupa, ģenerēta no 0 - ce H 1 tikai viens elements (neitrāls elements).
b. Cikliska apakšgrupa, kas izveidota, pamatojoties uz 1, - ce H4, kā pati grupa G.
1 0 mod 6 = 0 1 1 mod 6 = 1 1 2 mod 6 = (1 + 1) mod 6 = 2 1 3 mod 6 = (1 + 1 + 1) mod 6 = 3 1 4 mod 6 = (1 + 1 + 1 + 1) mod 6 = 4 1 5 mod 6 = (1 + 1 + 1 + 1 + 1) mod 6 = 5
iekšā. Cikliskā apakšgrupa, kas ģenerēta, pamatojoties uz 2 - tse H 2, un tai var būt trīs elementi: 0, 2 un 4.
2 0 mod 6 = 0 2 1 mod 6 = 2 2 2 mod 6 = (2 + 2) mod 6 = 4
d. Cikliskā apakšgrupa, kas ģenerēta, pamatojoties uz 3 — ce H 3, jo tai var būt divi elementi: 0 un 3.
e) cikliskā apakšgrupa, kas izveidota, pamatojoties uz 4 - H 2 ; tse nav jauna apakšgrupa.
4 0 mod 6 = 0 4 1 mod 6 = 4 4 2 mod 6 = (4 + 4) mod 6 = 2
e. Cikliskā apakšgrupa, kas izveidota, pamatojoties uz 5, - ce H 4, uzvarēja - pati G grupa.
5 0 mod 6 = 0 5 1 mod 6 = 5 5 2 mod 6 = 4 5 3 mod 6 = 3 5 4 mod 6 = 2 5 5 mod 6 = 1
Krājums 5.8
No grupas var ņemt trīs cikliskās apakšgrupas. G maє tilki chotiri elementi: 1, 3, 7 un 9. Cikliskās apakšgrupas - ![]()
![]() ka . Zemāk ir parādīts, kā ir zināmi apakšgrupas elementi.
ka . Zemāk ir parādīts, kā ir zināmi apakšgrupas elementi.
a. Cikliskā apakšgrupa, kas izveidota, pamatojoties uz 1, - ce H1. Apakšgrupā ir tikai viens elements, un tā pati ir neitrāla.
b. Cikliskā apakšgrupa, kas ģenerēta, pamatojoties uz 3, - ce H3, tāpat kā grupa G.
3 0 mod 10 = 1 3 1 mod 10 = 3 3 2 mod 10 = 9 3 3 mod 10 = 7
iekšā. Cikliskā apakšgrupa, kas ģenerēta, pamatojoties uz 7, - ce H3, kā arī grupa G.
7 0 mod 10 = 1 7 1 mod 10 = 7 7 2 mod 10 = 9 7 3 mod 10 = 3
d) cikliskā apakšgrupa, kas izveidota, pamatojoties uz 9, - ce H2. Apakšgrupā var būt tikai divi elementi.
9 0 mod 10 = 1 9 1 mod 10 = 9
Cikliskās grupas
Cikliskā grupa- Grupa, piemēram, suverēna cikliska apakšgrupa. 5.7. sadaļā grupai var būt cikliska apakšgrupa H 5 \u003d G. Tse nozīmē, ka grupa G ir cikliska grupa. Kādā veidā elements, kas ģenerē ciklisku apakšgrupu, var ģenerēt arī grupu. Šim elementam ir dots nosaukums "ģenerators". Tāpat kā g - ģenerators, beigu cikliskās grupas elementus var rakstīt kā
(e, g, g 2, ....., g n-1), de g n = e.
Ar cieņu, ciklu grupa var radīt daudz ģeneratoru.
Krājums 5.9
a. G grupa =
b. Grupa - cikliska grupa ar diviem ģeneratoriem, g = 3 un g = 7 .
Lagranža teorēma
Lagranža teorēma parāda atšķirību starp grupas secību un apakšgrupas secību. Pieņemsim, ka G ir grupa un H ir G apakšgrupa. Tāpat kā secība G un H - |G| un |H| , derīgs, derīgs līdz teorēmai |H| dalīties | G | . Pieteikumam 5.7 | G | = 6. Apakšgrupu secība - | h1 | = 1, | H2 | = 3, | H3 | = 2 un |H4| = 6. Acīmredzot visi pasūtījumi ir dilņiks 6 .
Lagranža teorēmā var būt vairāk nekā daži papildinājumi. Ja ir dota grupa G, tad її secība | G | , var viegli piešķirt potenciālo apakšgrupu pasūtījumus, lai jūs zinātu dilnikus. Piemēram, grupas G secība =
Elementu secība
Elementu secība grupas secībai (a) (kārtībai (a)) ir vismazākais veselais skaitlis n, lai a n = e . Citiem vārdiem sakot: elementa secība ir grupas secība, kas ir veids, kā tas tiek ģenerēts.
Krājums 5.10
a. G grupa =
b. G grupa =
- 1. Grupa Z veseli skaitļi no locīšanas darbības.
- 2. Visu soļa sarežģīto sakņu grupa n no viena līdz reizināšanas darbībai. Oskilki cikliskā skaitļa izomorfisms
grupa ir cikliska un elements ir izveidots.
Mans bachimo, ka cikliskās grupas var būt gan endēmiskas, gan nesintētiskas.
3. Sanāk - laba grupa un laba stihija. Bagato ir cikliska grupa ar apmierinošu elementu g. To sauc par ciklisku apakšgrupu, ko ģenerē elements g, un šī secība ir elementa g secība. Saskaņā ar Lagranža teorēmu elementa secība ir grupas paplašinātājs. Fermentācija
kas slēpjas aiz formulas:
Acīmredzot pēc homomorfisma šis її attēls ir zbіgaєtsya. Vidobrazhennya ir surjektīvi vienāda un mazāk tāda pati, ja grupa G- ciklisks g Es izveidoju elementu. Kuru veidu sauc par standarta homomorfismu cikliskajai grupai G ar savītu vijumu g.
Zastosuchi šādā veidā teorēmu par homomorfismu, mēs ņemam vērā ciklisko grupu spēka nozīmi: vai cikliskā grupa ir homomorfiska pakāpe. Z .
Izveidojiet kādu grupu G var tikt iecelts solis elements ar vairākām norādēm:
Lai varas vieta
Tse acīmredzot, yakscho . Paskatīsimies uz vipadoku, ja . Todi
Līdzīgi tiek aplūkotas arī citas tendences.
З (6) kliedz, sho
Krіm turklāt par iecelto. Šādā secībā elementa līmenis nosaka grupas apakšgrupu G. Vonu sauc cikliskā apakšgrupa, ko ģenerē elements, un ir norādīts caur .
Principā ir iespējamas divas atšķirības: vai nu visi elementa posmi ir atšķirīgi, vai ne. Pirmajā tipā apakšgrupa nav izdilis. Apskatīsim vēl vienu aspektu.
Aiziet ,; tas pats. Vismazāk no naturālajiem skaitļiem t, tiem, kas tā aicināti kārtībā elements i ir norādīts caur .
1.priekšlikums. Jakšo , tad
pierādījums. 1) Sadalīt m uz P par daudz:
Izejiet noteikto pasūtījumu
Sakarā ar uz priekšu
Pēdējais. Jakščo, apakšgrupa mo atriebība n elementi.
Pierādījums. Tiesa,
turklāt visi elementi ir atšķirīgi.
Tam ir vipadka, ja jums tādas nav t, scho (tobto var būt pirmais no iepriekš minētajiem aprakstiem), vvazhayut . Vidmitimo, scho; visu pārējo grupas elementu kārtas ir lielākas par 1.
Piedevu grupā mēs nerunājam par elementa pakāpi , par jogu daudzkārtēji jaki nozīmē cauri . Atkarībā no piedevu grupas elementa secības G- mazākais no naturālajiem skaitļiem t(kā zināms), tiem
PIETEIKUMS 1. Lauka raksturlielums ir jebkura elementa, kas nav nulle, secība i-tajā piedevu grupā.
BUTS 2. Ir skaidrs, ka kіntsevoi grupai ir jebkura kіtsevy elementa secība. Tiks parādīts, kā tiek aprēķināta elementu secība grupā.Aizvietošana tiek izsaukta cikls dozhini un apzīmē caur yakscho uzvarēja cikliski pārkārtot
un reshta viscaur. Ir skaidrs, ka cikla secība ir labāka nar. Cikli i sauc neatkarīgs, pat starp skaitļiem, kurus viņi faktiski pārkārtojuši, nav daudz nežēlīgu; kurā virzienā . Vai tas būtu kā aizstāšana, tas ir nepārprotami izklāstīts neatkarīgo ciklu TV. Piemēram,
kas ir skaidri parādīts mazajam, kas ir attēlots ar bultiņām. Šādi aizstāšana tiek izkārtota neatkarīgu dožinu ciklu TV , tad
PIETEIKUMS 3. Kompleksā skaitļa secība kіnceviy grupā ir pāra un tikai taisnīga, ja skaitlis ir vienas un tās pašas vienotības pasaules sakne, tātad, savā melnā krāsā, dažādi, vēl vairāk, ja, a porіvnyаєmo z, tobto. .
PIETEIKUMS 4. Mums ir zināmi dzīvokļa drupu grupas galīgās kārtas elementi. Aiziet. Jo kāda jēga ir jēga
griezties cikliski , kas tad ir smaguma centrs par nepaklausīgs schodo. Otzhe, - vai vērsties pie prāta griezuma ap punktu par, pretējā gadījumā vajadzētu būt iespējai taisnai līnijai iziet cauri par.
BUTS 5. Mēs zinām matricas secību
kā grupas elements. Maymo
nu ko. Acīmredzot šis dibens ir īpaši izvēlēts: iespēja, ka matricas panākumu secība būs galīga, vairāk vienāda ar nulli.
2.priekšlikums. Jakšo , tad
Pierādījums. Aiziet
nu ko. Maymo
Tēvs,.
Tikšanās 1 . Grupa G sauca ciklisks kā izmantot šādu elementu , kas . Tādu elementu sauc vecāku elements grupai G.
PIETEIKUMS 6. Aditīva veselu skaitļu grupa ir cikliska, fragmentus ģenerē elements 1.
PIETEIKUMS 7. Moduļa atbalsta papildu grupa nє ciklisks, šķembas ģenerē elements.
PIETEIKUMS 8. N-tā soļa kompleksās saknes reizinātāja grupa ar 1 є ciklisku. Patiešām, skaitļu saknes būtība
Skaidrs par ko . No tās pašas grupas tiek ģenerēts elements.
Ir viegli bachiti, kas ir neizsmeļamā cikliskā elementu grupā, ko var ģenerēt, tikai daži. Tātad grupā Z vecāku elementi ir vairāk nekā 1 un - 1.
Elementu skaits gala grupā G sauc par її kārtībā viņa ir norādīta caur. Beigu cikliskās grupas secība ir tāda pati kā ģenerētā elementa її secība. Uz to no 2. priekšlikuma raud
3.priekšlikums . Cikliskās grupas elements rīkojums n ģenerē dažus un tikai dažus, ja
PIETEIKUMS 9. Grupas vecāku elementi tiek saukti primārās saknes n solis no 1. Tā ir prāta sakne , de. Piemēram, 12. soļa pirmā sakne no 1.
Cikliskās grupas ir visvienkāršākās grupas, lai jūs varētu sevi identificēt. (Īpaši ābeliešu smaka.) Nākamā teorēma sniedz savus jaunos aprakstus.
1. teorēma. Vai bezgalīgi cikliska grupa ir izomorfa grupa. Kā Kіntsev cikliskā grupa ir n kārtas izomorfa grupai.
pierādījums. Tā kā tā ir nelobīta cikliska grupa, tad caur formulu (4) tā ir izomorfisms.
Ejam - kіntseva tsiklіchna grupa kārtībā P. Mēs skatāmies uz attēlu
tad displejs ir pareizi un objektīvi piešķirts. jauda
viplyvaє іz tієї zh formula (1). Šajā rangā - izomorfisms.
Teorēma ir pabeigta.
Grupas izpratnei svarīga loma ir apakšgrupas zināšanām. Visas cikliskās grupas apakšgrupas var viegli aprakstīt.
Teorēma 2. 1) Esiet cikliskas grupas apakšgrupa.
2) Cikliskā grupa ir sakārtota n pasūtiet, vai koplietot apakšgrupas n i jebkuram dilnik q skaitlim n Ir tieši viena q kārtas apakšgrupa.
pierādījums. 1) Nehai - cikliskā grupa i H- її apakšgrupa, vіdminna vіd (viena apakšgrupa, protams, є cikliska.) . Aiziet t- vismazākais no naturālajiem skaitļiem tiem . Paziņojiet mums to . Aiziet . Podilimo pirms tam uz t par daudz:
zvaigznes no noteiktā datuma t nākamais, scho th, vēlāk, .
2) Jakšo , tad uz priekšu mirkuvannya, zastosovane līdz ), parādi ko . Ar ko
і Hє vienas apakšgrupas pasūtījums q grupā G. Atpakaļ, jakšo q- esi skaitļa dilniks Pі , tad pakārtoti H, vynachaetsya līdzsvars (9), apakšgrupu secība q. Teorēma ir pabeigta.
Sekas . Vienkāršā secībā cikliskā grupā, neatkarīgi no tā, vai tā nav viena, apakšgrupa darbojas kopā ar otru grupu.
PIETEIKUMS 10. Grupā, vai tā būtu apakšgrupa, varu paskatīties, de.
PIETEIKUMS 11. n-tā soļa sakņu grupā z 1 ir sakņu grupas apakšgrupa q- solis no 1, de.
Apskatīsim visu vai divu soļu reizināšanas grupu no diviem (2Z, ), de 2Z = (2n | P e Z). Piedevas my є grupas analogs ir veselu dvīņu aditīvu grupa (2Z, +), 2Z = (2n | p e Z). Damo zagalne vyznachennya grupas, okremi butts šādas є danі grupas.
Tikšanās 1.8. Multiplikatīva grupa (G,) (Piedevu grupa (G, +)) tiek saukta ciklisks it kā to saskaita no viena elementa nepieciešamā soļu skaita (atkarībā no punktu skaita). a e G, tobto. G=(A p | p e Z) (vіdpovidno, G - (pa | p e Z)). Apzīmējums: (a), lasiet: cikliskā grupa, ko ģenerē elements a.
Apskatīsim to.
- 1. Mērogojošas reizināšanas cikliskās grupas apakšdaļa var būt visu fiksēta vesela skaitļa cikla soļu grupa. a f±1, vinnēts norādīts un r. tādā veidā, un d — (a).
- 2. Multiplikatīvās termināla cikliskās grupas sadursme ir n-tā soļa sakņu grupa C no vienības. Uzminot, ka n-tā soļa sakne ir viena
aiz formulas e k= cos---hisin^-, de pirms = 0, 1, ..., P - 1. Slaids- lpp. lpp
tiešām, З„ = (е x) = (е x = 1, e x, ef = e 2 ,..., e "-1 =? „_ x). Mēs domājam, ka kompleksie skaitļi e uz, uz = 1, ..., P - 1, ir attēloti ar viena mieta punktiem P vienādās daļās.
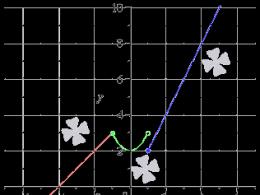
- 3. Raksturīgs piemērs aditīvai nemērogojošai cikliskai grupai ir aditīva veselu skaitļu grupa Z, ko ģenerē skaitlis 1, tas ir. Z = (1). Ģeometriski tas parādās, redzot visus skaitliskās līnijas punktus. Faktiski šādi tiek attēlota pati multiplikatīvā grupa 2 7 - = (2) a z \u003d (a), deciļskaitlis a f±1 (div. 1.3. att.). Attēlu kvalitāte ir aplūkota 1.6. punktā.
- 4. Vibero lielā reizināšanas grupā G aktīvais elements a. Tad visi elementa soļu cikli apmierina ciklisko apakšgrupu (a) = (a lpp Z)G.
- 5. Var parādīt, ka racionālo skaitļu aditīvā grupa Q pati par sevi nav cikliska, bet gan neatkarīgi no tā, vai cikliskajā apakšgrupā atrodas divi elementi.
A. Mēs pierādam, ka piedevu grupa Q nav cikliska. Pieļaujami nepieņemami: lai Q = (-). Pamata mērķa numurs b,
nedalīties tie. Oskіlki - eQ = (-) = sn-|neZ>, tad esošais
b t/ (t Dž
є tsile numurs gs 0, tātad - = n 0 -. Ale todi m = n 0 kb
zvaigznes t:- dіyshli super-asums.
B. Pieņemsim, ka divi diezgan racionāli skaitļi -
h „ /1
i - pārklāšanās cikliskā apakšgrupa (-), de t atrast- d t/
mazāks par lielu skaitļu daudzkārtni bі d. Pareizi, nedarīsim m-bi
, a 1 /1 h cv 1/1
i m = av, u, v e Z, tad i - = - = aї-e(-)i - = - = cv-e(-).
b b i t t/ a dv t t/
Teorēma 1.3. Cikliskās grupas secība ir tāda pati kā grupas vecākelementa tobto secība.|(a)| = | a |.
Pierādījums. 1. Nāc | = ">. Mēs zinām, ka visi elementa dabiskie soļi a savādāk. Pieļaujami nepieņemami: nāc a k = a tі 0 uz Todi t - pirms tam- naturāls skaitlis a t ~ līdz = e. Ale tse superechit uz to, scho | a = ° °. Tādā veidā visi elementa dabiskie soļi a raznі, zvіdki vyplivaє neskіchennіst grupa (a). Oche, | (a)| = ° ° = | a |.
2. Nāc | a | = n. (a) \u003d (e — a 0, a, a 2,..., a "-1). No cikliskās grupas apzīmējuma iekļaušana (a 0, a, a 2, ..., o" 1-1) s (a). Ieslēdzam to. Cikliskās grupas papildu elements a) var izskatīties a t, de ti Z. Pārmērīga šnabi dalīšana: m-nq + r, de 0 lpp Oskilki a n = e, tad a t = a p i + g \u003d a p h? a r = a r e(a 0, a, a 2,..., a "- 1). -1).
Ir jāpanāk, ka visi elementi tiek reizināti (a 0, a, a 2,..., un "-1) atšķiras. Pieļaujams nepieņemams: lai 0 i P, ale a" = a). Tas pats vīns - e ta 0 j - i - dіyshli super-asums z umovoy | a | = P. Teorēma ir pabeigta.