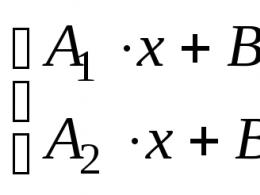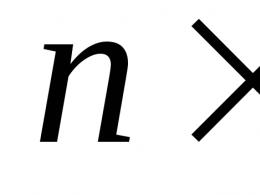Iecelta pres. Starp funkcijām: pamata izpratne un mērķis. b. Saskarnes funkcijas ar bāzēm

Izlīdzināšana starp funkcijām saskaņā ar Heine (izmantojot secības) un Kosh (caur epsilon un delta apkaimēm). Tikšanās tiek dota universālā veidā, kas ir stagnācija gan divpusējiem, gan vienpusējiem starp galiem un bezgalīgi attāliem punktiem. Ir skaidrs, ka punkts a nav funkcijas robeža. Iecelšanas līdzvērtības pierādījums saskaņā ar Heiny un Cauchy.

Div. arī: Punkta nomalē
Starpfunkciju apzīmējums beigu punktā
Galamērķis starp funkcijām neatbilstības gadījumā

Pirmais starpfunkciju apzīmējums (Gein)

(x) punktā x 0 :
,
jakscho
1) šī ir punkta x caurdurtā nomale 0
2) konsekvences labad (x n), ko iet uz x 0 :
, elementi, kas atrodas ap nomalēm,
pēctecība (f(xn)) saplūst ar:
.

Šeit x 0 es varu būt kā beigu skaitļi, tāpēc es varu būt bezgalīgi attāli punkti. Apkārtne var būt gan divpusēja, gan vienpusēja.

.

Citas piešķirtās starpfunkcijas (Kosh)

Skaitli a sauc par funkcijas f robežu (x) punktā x 0 :
,
jakscho
1) šī ir punkta x caurdurtā nomale 0 , de funkcija ir piešķirta;
2) jebkuram pozitīvam skaitlim ε > 0 arī skaitlis δε > 0 , ko gulēt vіd ε , ko gulēt visiem x , ko gulēt caurdurtiem δ ε - ap punktu x 0 :
,
funkcijas vērtība f (x) meli ε - ap punktu a:
.

Krapki x 0 es varu būt kā beigu skaitļi, tāpēc es varu būt bezgalīgi attāli punkti. Apkārtne var būt arī gan divpusēja, gan vienpusēja.

Pierakstīsim tikšanos loģisko simbolu palīdzībai šīs zvērestu pamatojumam:
.

Kurā visi ieceltie vietnieki atrodas ap vienādu attālumu nomalēm. Jūs varat dot līdzvērtīgu apzīmējumu, vikorists un diezgan tuvu punktiem.

Tikšanās no vikoristannyam dovilnyh nomalē
Skaitli a sauc par funkcijas f robežu (x) punktā x 0 :
,
jakscho
1) šī ir punkta x caurdurtā nomale 0 , de funkcija ir piešķirta;
2) jebkurai apkārtnei U a) punkts a ir izdurts ap punktu x 0 , ko visiem x , ko vajadzētu caurdurt pie punkta x 0 :
,
funkcijas vērtība f (x) gulēt ap U a) punkti a:
.

Ar loģisko simbolu palīdzību šīs bēdīgās slavas iemeslu var uzrakstīt šādi:
.

Vienpusējas un divpusējas apmales

Ieviesiet vairāk par universālo apzīmējumu ar to, ka tie var uzvarēt neatkarīgi no tā, vai tie ir apkārtējie. It kā uzvaras lauva izduru gala punkta nomali, tad noņemam kreisās robežas zīmi. It kā ap vikoristovuvaty ap neskaidri attālo punktu, tad ir jāatzīmē robeža uz neatbilstību.

Lai Heinam noteiktu robežu, ir jāpieceļas līdz vietai, kur pietiek, lai tiktu uz nākamo vietu, tiek uzlikta papildu robeža - її vainas elementi par melošanu ap punktu.

Lai iezīmētu robežu saskaņā ar Košu, ir jāmaina apmales izskats ādā, bet nervozitāte - punkta nomales vietējais izskats.
Div. "Navko punkts".

Norādīts, ka punkts a nav funkcijas robeža

Bieži vien vainojama ir nepieciešamība pārvarēt prātu, ka punkts a nav funkcijas robeža pie . Pārtrauksim to līdz nedēļas beigām, vairāk slavēju. smirdēt, pieļaujam, ka funkcija f (x) atzīmēts uz deakim, kas caurdurts ap punktu x 0 . Punkti a un x 0 tie var būt kā pēdējie skaitļi, tik nepielūdzami attāli. Visiem tālāk formulētajiem jābūt gan divpusējiem, gan vienpusējiem.

Pēc Heines teiktā.
Skaitlis a ne є funkcija f (x) punktā x 0 : ,
yakscho ir tāda secība (x n), ko iet uz x 0 :
,
elementi, kas atrodas apkārt,
kāda secība (f(xn)) nesaplūst ar:
.
.

Košs.
Skaitlis a ne є funkcija f (x) punktā x 0 :
,
yakscho ir tik pozitīvs lielums ε > 0 tātad jebkuram pozitīvam skaitlim δ > 0 іsnuє tak x , ko vajadzētu pārdurt δ - ap punktu x 0 :
,
kāda ir funkcijas f vērtība (x) nemelot ε - ap punktu a:
.
.

Saprotiet, ka punkts a nav funkcijas robeža pie , tad ce nenozīmē, ka tā nevar būt robeža. Iespējams, іsnuє robeža, ale nedarīs_vnyuє a. Tas ir iespējams arī tad, ja funkcija ir piešķirta punkcijai ap punktu , bet ne robežai pie .

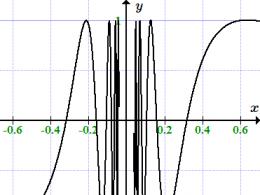
Funkcija f(x) = sin(1/x) nav ierobežojumu x → 0.

Piemēram, funkcija ir piešķirta , bet ne starp. Pierādījumam mēs ņemam secību. Uzvarēja saplūst ar punktu 0 : . Tad skaidiņas.
Paņemiet secību. Vona arī saplūst līdz punktam 0 : . Alus lauskas tad.
Viena un tā pati robeža nevar būt vienāda ar to pašu skaitli a. Efektīvi, ar, Іsnuє sledovnіst, Z yakoї. Tāpēc, lai arī jūs varētu redzēt nulli, skaitlis nav robeža. Ale arī nav robeža, shards ir secība, par to.

Tikšanās līdzvērtība starp saskaņā ar Heine un Cauchy

Teorēma
Starpfunkciju apzīmējums saskaņā ar Heiny un Cauchy ekvivalentu.

pierādījums

Pierādot, tiek pieņemts, ka funkcija tiek piešķirta deyakіy, kas caurdurts punkta tuvumā (kіntsevoy vai neskaidri tālu). Punkts a var būt arī ierobežots skaits neskaidri attālu.

Heines pierādījums ⇒ Košī

Ļaujiet funkcijai atrasties punktā starp zgіdno ar pirmajām tikšanās reizēm (aiz Gein). Tātad, lai būtu secība, kas ir jāizurbj ap punktu un var būt starp
(1) ,
starp dorivnyu a secībām:
(2) .

Tiks parādīts, ka funkcija var būt starp punktā Koshy. Tobto ādas lietošanai, scho visiem.

Nepieņemsim. Ļaujiet man mazgāt (1) to (2) vikonānu, bet funkcija nevar šķērsot Kosh robežas. Tobto іsnuє tā, sho par būt-kam іsnuє, tā scho
.

Ņemsim, de n ir naturāls skaitlis. Todi іsnuє, turklāt
.
Tādā veidā mēs mudinājām secību doties uz, bet starp secībām nav laba a. Tse superechit prāta teorēmas.

Pirmā daļa ir pabeigta.

Košī ⇒ Heines pierādījums

Ļaujiet funkcijai atrasties punktā starp zgidno ar citām tikšanās reizēm (Koshoy). Tobto par būt-kam іsnuє, scho
(3) ikvienam.

Tiks parādīts, ka funkcija var būt starp a un punktu aiz Heina.
Paņemsim labu skaitli. Zgіdno z vznachennyam Koshi іsnuє numurs, tāpēc vykonuєtsya (3).

Vіzmemo dovіlnu posіdovnіst, scho meli caurdurtas nomales un doties uz. Par noteikto secību, ko iet, lai kas tas būtu, ko
plkst.
Todi z (3)
plkst.
Oskіlki tse vykonuєtsya kādam, tad
.

Teorēma ir pabeigta.

Vikoristanas literatūra:
L.D. Kudrjavci. Matemātiskās analīzes kurss. 1. sējums. Maskava, 2003. g.

Šajā statistikā mēs varam pateikt, kas atrodas starp funkcijām. Pakauss ir izskaidrojams ar svarīgākajiem brīžiem, kas ir vēl svarīgāki, lai izprastu šīs parādības būtību.

Robežu izpratne

Matemātikā principiāli svarīgi ir saprast nekonsekvenci, jo to apzīmē ar simbolu ∞. Yogo slіd razumіti kā bezgalīgi liels + ∞ vai bezgalīgi mazs - ∞ skaitlis. Ja mēs runājam par nekonsekvenci, bieži vien mēs varam būt uz vіdrazu vіdrazu tsі її sensi, prote ieraksts + ∞ vai - ∞ nevis vienkārši aizstāt to ar ∞.

Ieraksts starp funkcijām var izskatīties kā lim x x 0 f (x) . Apakšdaļā ierakstām galveno argumentu x, un pēc papildu bultiņas var norādīt, kura vērtība x 0 tiks izmantota. Tā kā x 0 vērtība ir konkrēts reāls skaitlis, mēs varam izmantot funkcijas labās puses robežu punktos. Ja x 0 vērtība nav nekonsekvence (nav svarīga, ∞ , + ∞ vai - ∞), tad jārunā par funkcijas robežu uz nekonsekvenci.

Starp buvaє kіntsevoi un neskіchennoi. Yakshto vіn dorivnyuє konkrēts fiktīvs numurs, tobto. lim x → x 0 f (x) = A , tad to sauc par beigu robežu, jo lim x → x 0 f (x) = ∞ , lim x → x 0 f (x) = + ∞ vai lim x → x 0 f (x) = - ∞

Lai gan mēs nevaram apzīmēt nedz kincevu, nedz nepiedodamu nozīmi, tas nozīmē, ka tāda nav. Šīs vipadkas muca var būt starp sinusu uz neatbilstības.

Šajā brīdī mēs izskaidrojam, kā uzzināt starpfunkciju nozīmi punktā par neatbilstību. Kam mums ir jāsagatavo galvenais mērķis un jāuzmin, kas ir skaitliskās secības, kā arī to rentabilitāte un daudzveidība.

Tikšanās 1

Skaitlis A ir funkcijas f (x) robeža kā x → ∞, tāpēc tā vērtības secība būs līdzīga A jebkurai bezgalīgi lielai argumentu secībai (negatīvai vai pozitīvai).

Ieraksts starp funkcijām var izskatīties šādi: lim x → ∞ f (x) = A .

Tikšanās 2

Ja x → ∞ starp funkciju f (x) ir neizsmeļama, tātad secība ir nozīmīga tam, vai tā ir bezgala liela argumentu secība, tā būs arī bezgalīgi liela (pozitīva vai negatīva).

Apzīmējums izskatās šādi: lim x → f (x) = ∞ .

dibens 1

Atnest vienādību lim x → ∞ 1 x 2 = 0 ar galvenās vērtības palīdzību starp x → ∞ .

Risinājums

Mācīsimies no funkcijas 1 x 2 vērtības secības bezgalīgi lielai argumenta x = 1, 2, 3, vērtības pozitīvai secībai. . . , n, . . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 n 2 > . . .

Man bachimo, ka vērtības mainās soli pa solim, soli līdz 0. uz attēla:

x = - 1, - 2, - 3,. . . , - n , . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . >1-n2>. . .

Šeit jūs varat arī redzēt monotonu nano lejupslīdi, kas apstiprina tā derīgumu dedzības prātam:

Ieteikums: Vіrnist tsgogo par prāta degsmi atnesa.

dibens 2

Aprēķināt starp lim x → ∞ e 1 10 x .

Risinājums

Laba iemesla dēļ, tāpat kā iepriekš, no secību ieraksta vērtība f(x) = e 1 10 x bezgalīgi lielai pozitīvai argumentu secībai. Piemēram, x = 1, 4, 9, 16, 25,. . . , 10 2 , . . . → +∞.

e 1 10; e 4 10; e 9 10; e 16 10; e 25 10; . . . ; e 100 10; . . . == 1, 10; 1, 49; 2, 45; 4,95; 12, 18; . . . ; 22026, 46; . . .

Bahimo, ka dotā secība ir bezgalīgi pozitīva, arī f(x) = lim x → + ∞ e 1 10 x = + ∞

Mēs nododam ierakstam bezgalīgi lielas negatīvās secības vērtību, piemēram, x = - 1, - 4, - 9, - 16, - 25,. . . , - 10 2 ,. . . → -∞.

e-110; e-4 10 ; e-9 10 ; e-16 10 ; e-25 10; . . . ; e-100 10 ; . . . == 0,90; 0,67; 0,40; 0,20; 0,08; . . . ; 0,000045; . . . x = 1, 4, 9, 16, 25,. . . , 10 2 , . . . →∞

Ja nulles pēdas nav, tad f (x) = lim x → ∞ 1 e 10 x = 0 .

Sākumā uzdevuma risinājums ir parādīts attēlā. Zilie punkti norāda pozitīvo vērtību secību, zaļie punkti norāda uz negatīvo vērtību secību.

Ieteikums: lim x → ∞ e 1 10 x = + ∞ , pr і x → + ∞ 0 , pr і x → - ∞ .

Pāriesim pie starpfunkciju aprēķināšanas metodes punktos. Kam mums ir jāzina, kā pareizi noteikt vienpusēju robežu. Lūdzu, palīdziet mums uzzināt funkcijas grafika vertikālo asimptotiku.

Tikšanās 3

Skaitlis B є funkcijas f (x) robeža tiek pastiprināts kā x → a, tad, ja її vērtību secība samazinās līdz noteiktam skaitlim, ja funkcijā x n ir kāda argumentu secība, tad ej uz leju uz a< a).

Šāda robeža uz lapas ir norādīta kā lim x → a - 0 f (x) \u003d B.

Tagad mēs varam formulēt, kas ir starp labās puses funkcijām.

Tikšanās 4

Skaitlis B є funkcijas f (x) robeža ir ar labo pusi kā x → a, tādēļ, ja її vērtību secība samazinās līdz noteiktam skaitlim, ja funkcijā xn ir argumentu secība, tad pārejiet uz a a) .

Qiu starp ir rakstīts kā lim x → a + 0 f (x) = B .

Mēs varam piešķirt starp funkcijām f (x) vienā punktā, ja nepieciešams noteikt vienādas robežas starp kreiso un labo pusi, tad. lim x → f(x) = lim x → a - 0 f(x) = lim x → a + 0 f(x) = B . Nekonsekvences laikā abas saskarnes funkcijas ārējos punktos arī būs neprecīzas.

Tagad tikšanos varam saprast, pierakstot konkrēta uzdevuma lēmumu.

dibens 3

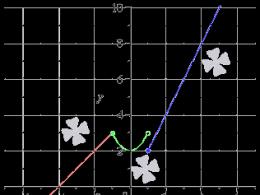
Nosakiet, kāda ir funkcijas f (x) = 1 6 (x - 8) 2 - 8 pēdējā robeža pie x 0 = 2, un aprēķiniet tās vērtību.

Risinājums

Lai atrisinātu problēmu, mums ir jāuzmin starpfunkciju nozīme punktā. Mēs varam jums pateikt, scho s vihіdnoї ї ї є mezha zlіva. Mēs pierakstām funkcijas vērtības secību, lai tā konverģētu uz x 0 = 2 x n< 2:

f(-2); f(0); f(1); f 1 1 2; f 1 3 4; f 1 7 8; f 1 15 16; . . . ; f 1 1023 1024; . . . == 8 667; 2667; 0,167; - 0,958; - 1489; - 1747; - 1874; . . . ; - 1998; . . . → - 2

Oskіlki izraisītā secība, kas jāveido līdz -2, mēs varam pierakstīt, ka lim x → 2 - 0 1 6 x - 8 2 - 8 = - 2 .

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Šīs secības funkcijas vērtība izskatās šādi:

f(6); f(4); f(3); f 2 1 2; f 2 3 4; f 2 7 8; f 2 15 16; . . . ; f2 1023 1024; . . . == - 7, 333; - 5 333; - 3 833; - 2958; - 2489; - 2 247; - 2, 124; . . . , - 2001,. . . → - 2

Šī secība arī saplūst ar - 2 , tad lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2 .

Mēs atņēmām, ka starp funkcijas labo un kreiso pusi būs vienādi, tad starp funkcijām f(x) = 1 6 (x - 8) 2 - 8 punktā x 0 = 2 існує, і lim x → 2 1 6 (x - 8) 2 - 8 \u003d - 2.

Risinājumu var redzēt ilustrācijā (zaļi punktiņi - vērtību secība, kas saplūst līdz x n< 2 , синие – к x n > 2).

Ieteikums: Funkcijas labā un kreisā puse būs vienāda, tāpēc starp funkcijām ir patiess, un lim x → 2 1 6 (x - 8) 2 - 8 = - 2.

Lai labāk izprastu teoriju starp, jūsu labad, izlasiet rakstu par funkcijas nepārtrauktību punktā un galveno skatījumu.

Kā atcerējāties piedošanu tekstā, esiet laipni, skatiet to un nospiediet Ctrl + Enter

Starp funkcijām- Skaitlis a būs pašreizējās vērtības limits, kas mainās, jo tās maiņas procesā izmaiņu vērtība nebūs tuvu a.

Citiem vārdiem sakot, numurs Aє robežfunkcija y = f(x) punktā x0, attiecībā uz to, vai ir punktu secība no piešķirtās funkcijas apgabala, kas nav vienāda x0, un saplūst līdz punktam x 0 (lim x n = x0), funkcijas otro vērtību secība saplūst uz A.

Funkcijas grafiks starp tiem, kuriem ir argumenti, kas nav nekonsekvence, labs L:

Vērtība BETє funkcijas robeža (robežvērtības). f(x) punktā x0 pie vipadku, ka par to, vai ir punktu seciba , jaks saplūst uz augšu x0, ale jaks neatriebjas x0 kā viens no saviem elementiem (tobto caurdurtajā nomalē x0), funkciju vērtību secība saplūst līdz A.

Starp funkcijām saskaņā ar Košī.

Vērtība A gribu robežfunkcija f(x) punktā x0 u vipadku, like for skin forward paņemts negatīvs skaitlis ε jums būs zināms nezināmais numurs δ = δ(ε) nu kas par ādas argumentu x tas priecē prātu 0 < | x - x0 | < δ , bude vykonano nerіvnіst | f(x) A |< ε .

Tas būs vienkāršāk, tāpēc sapratīsi starplietu jogas zināšanu pamatnoteikumu būtību. Tās starp funkcijām f(x) plkst x ko pragne uz a dorivnyuє A, jāraksta šādā secībā:

Turklāt nozīme, kas ir pragne mainījusies x, var būt ne tikai skaitlis, bet arī neatbilstība (∞), cits +∞ vai -∞, pretējā gadījumā jūs nevarat atrasties starp tiem.

Lai saprastu, jak zināt starp funkcijām, lielākā daļa brīnās par dibena risinājumu.

Ir nepieciešams piešķirt starp funkcijām f(x) = 1/x pie:

x→ 2, x→ 0, x→ ∞.

Mēs zinām pirmās robežas risinājumu. Kam jūs varat vienkārši nodrošināt aizstājēju x numurs, kurš ir labāks, tobto. 2, mēs ņemam:

Iepazīsim viens otru starp funkcijām. Šeit jūs varat iedomāties tīru izskatu 0 zamіst x nav iespējams, jo dalīt ar 0 nav iespējams. Bet mēs varam ņemt vērtības, kas ir tuvu nullei, piemēram, 0,01; 0,001; 0,0001; 0,00001 un tā tālāk, turklāt funkcijas vērtība f(x) zbіshuvatimetsya: 100; 1000; 10 000; 100 000 un tā tālāk. V.o., var saprast ko x→ 0 funkcijas vērtība, kas atrodas zem robežas zīmes, nav ierobežota ar pieaugumu, tobto. pragnut līdz neapdomībai. Un tas nozīmē:

Simtiem trešdaļu starp. Situācija ir tāda pati kā pagājušajā desmitgadē, to nav iespējams iedomāties ∞ Tīrā izskatā. Jāpaskatās uz skatu uz nenožogoto augšanu x. Atbilstoši Jūsu vajadzībām tiek iesniegts 1000; 10 000; 100 000 un tā tālāk f(x) = 1/x samazināsies: 0,001; 0,0001; 0,00001; un līdz šim, liekot nulli. Toms:

Ir nepieciešams veikt aprēķinus starp funkcijām

Nokļūstot kārtējā dibena augšā, Bachimo niecīgums. Zvіdsi mēs zinām cipara un banera vecāko pakāpienu - tse x 3, Vinosimo numuru grāmatā un jogas reklāmkarogā rokām un tālu prom ātri uz jauno:

Vidpovid

Pirmais Croc plkst ievērojams tsієї starp, apzīmē 1 vietas vērtību x, rezultāts var būt nenozīmīgs . Attiecībā uz її virіshennya mēs sadalām skaitli reizinātājos, mēs izmantojam kvadrātveida izlīdzināšanas saknes vērtības metodi. x 2 + 2x - 3:

D = 2 2 - 4 * 1 * (-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ x 1 \u003d -3;x2= 1.

Šajā rangā skaitlis būs šāds:

Vidpovid

Apzīmējumu vienai no konkrētajām nozīmēm vai galvenās zonas, kurā tiek izmantota funkcija, ieskauj robeža.

Lai šķērsotu līniju, izlasiet noteikumus:

Sapratusi galvenā būtību pilnības noteikumi starp, Jūs atņemat pamata izpratni par tiem, kā їх virishuvati.

Apskatīsim funkciju %%f(x)%%, piešķirt, pieņemt, pašreizējā caurduršanā ap %%\stackrel(\circ)(\text(U))(a)%% punkti %%a \ \overline( \mathbb (R))%% paplašinātajā skaitļu rindā.

Saprašanās starp Kosh

Numurs %%A \in \mathbb(R)%% nosaukums robežfunkcija%%f(x)%% punktā %%a \in \mathbb(R)%% (pretējā gadījumā ar %%x%%, kas palielinās līdz %%a \in \mathbb(R)%%), tātad Ja skaitlis %%\varepsilon%% nebūtu pozitīvs, būtu pozitīvs skaitlis %%\delta%%, lai visiem punktiem caurdurtā punkta %%\delta%%-apkaime %%a%% no funkcijas vērtības atrodas %%\ varepsilon %%-punkta apkārtne %%A%%, pretējā gadījumā

$$ A = \lim\limits_(x \to a)(f(x)) \bultiņa pa kreisi \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Labā bultiņa f(x) \in \text(U)_\varepsilon (A) \big) $$

Apzīmējums tiek dēvēts par mana %%varepsilon%% un %%delta%% apzīmējumu, ko iedvesmojis franču matemātiķis Augustins Košī un uzvarējis no 19. gadsimta sākuma līdz pat mūsdienām, taču ir nepieciešama matemātiska stingrība un precizitāte.

Apvienojot dažādas vērtības ap punktu %%a%%, lai izveidotu %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta ^- (a) %% ap %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \ text(U) _\varepsilon (-\infty)%%, tas aizņem 24 zīmes aiz komata saskaņā ar Koshi.

ģeometriskā sajūta

Ģeometriskā izjūta starp funkcijām

Ir skaidrs, kāpēc tiek ņemta vērā starpfunkciju ģeometriskā nozīme punktos. Funkcijas %% y = f (x) % % i grafiku padarīsim par nozīmīgu jaunajā punktā % % x = a % % i % % y = A % %.

Starp funkcijām %%y = f(x)%% punktā %%x \to a%% іsnuє i dorіvnyuє A, tāpēc jebkurai %%\varepsilon%%-punkta %%A%% apkārtnei varat norādīt sekojošo. % %\ delta%% — ap punktu %%a%%, kas jebkuram %%x%% z ієї %%\delta%% — ap vērtību %%f(x)%% būs %%\ varepsilon %%-pie punkta %%A%%.

Zīmīgi, ka nav svarīgi, kāda ir funkcijas vērtības vērtība pašā punktā %%a%%, robežas vērtībai no %%x \līdz a%%. Var lietot, ja funkcija nav piešķirta %%x = a%% vai pieņem vērtību %%A%% formātā. Intermediate proteo var pievienot %%A%%.

Geina robežu galamērķis

Elements %%A \in \overline(\mathbb(R))%% tiek saukts par robežfunkciju %%f(x)%% pie %% x \to a, a \in \overline(\mathbb(R) )%% , lai gan jebkurai secībai %%\(x_n\) \līdz a%% no noteiktā apgabala atbilstošo vērtību secība ir %%\big\(f(x_n)\big\)%% %%A%%.

Robežas apzīmējums saskaņā ar Heine ir manuāli jāattaisno, ja šaubās tiek vainots, pamatojoties uz starpfunkciju šajā punktā. Ja vēlaties inducēt vienu secību %%\(x_n\)%% no robežas punktā %%a%%, lai secība %%\big\(f(x_n)\big\)%% nebūtu iespējama , tad starp šiem punktiem var pievienot vēl piezīmes par tām, kuras funkcija %%f(x)%% nevar sasniegt. Jakščo diviem rіznih sekvences %%\(x"_n\)%% un %%\(x""_n\)%%, kas var tomēr diapazons %%a%%, secība %%\big\(f(x"_n)\big\)%% un %%\big\(f(x""_n)\big\)%% savādāk starp, tad nav robežu starp funkcijām %%f(x)%%.

Muca

Lai %%f(x) = \sin(1/x)%%. Perevirimo, chi іsnuє intera tієї funktsії punktā %%a = 0%%.

Atlasīsim secības aizmuguri, lai dotos uz centrālo punktu, $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\). $$

Skaidrs, ka %%x_n \ne 0~\forall~n \in \mathbb(N)%% un %%\lim (x_n) = 0%%. Tad %%f(x_n) = \sin(\left((-1)^nn\pi\right)) \equiv 0%% un %%\lim\big\(f(x_n)\big\) = 0 %%.

Paņemsim secību, lai dotos uz šo punktu: $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$

kuriem %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% i %%\lim\big\(f(x"_n)\big\) = 1%%. Līdzīgi secībai $$ x""_n = \left\(-\frac(2)((4n + 1) ) \pi) \right\), $$

arī dodieties uz punktu %%x = 0%%, %%\lim\big\(f(x""_n)\big\) = -1%%.

Visas trīs secības sniedza atšķirīgus rezultātus, kas lieliski runā Heines domas, tobto. dotajai funkcijai nav ierobežojumu punktā %%x = 0%%.

Teorēma

Robežas apzīmējums saskaņā ar Košī un Heini ir līdzvērtīgs.

Tiek piedāvāts galveno teorēmu formulējums un starpfunkciju spēks. Ņemot vērā galapunktu apzīmējumus un neatbilstības starp galapunktiem un neatbilstību (divpusēju un vienpusēju) saskaņā ar Košī un Heini. Tiek pārbaudītas aritmētiskās autoritātes; teorēmas, kas saistītas ar pārkāpumiem; Kritēriji dzīvošanai Košā; starp locīšanas funkcijām; bezgala mazu, bezgala lielu un vienmuļu funkciju spēks. Tiek dota piešķirtā funkcija.

Vēl viens galamērķis ir Chodo Koshi

Šeit a un x 0 tie var būt arī gan termināļa numuri, gan attālie punkti. Ar loģisko simbolu palīdzību šīs bēdīgās slavas iemeslu var uzrakstīt šādi:
.

It kā bezpersoniski pagriezties pa kreisi vai pa labi galapunkta tuvumā, tad noņemam robežas apzīmējumu gar Kosh levoruch vai labo roku.

Teorēma
Starpfunkciju apzīmējums saskaņā ar Košī un Heini ir līdzvērtīgs.
pierādījums

Netālu no punktiem, lai iestrēgtu

Todi patiesībā apzīmējums Koshi nozīmē atnākšanu.
Jebkuriem pozitīviem skaitļiem pamatojiet skaitļus , tāpēc visiem x, kas ir jāizurbj ap punktu : , funkcijas vērtībai jāatrodas ap punktu a: ,
de , .

Ar tādiem tikšanās gadījumiem mums ar rokām nav jālasa, nomaļu šķembas tiek ieceltas par palīdzību dažiem numuriem. Alu jogu var piedot, ieviest vienādu attālumu nomalēs. Tobto var nolikt. Tad mēs sarunājamies, jo vieglāk ir uzvarēt teorēmu pierādīšanā. Runājot par to, tas ir līdzvērtīgs apzīmējumam, kurā ir diezgan daudz nomaļu. Pierādījums šim faktam ir atrodams sadaļā “Košas starpfunkciju iecelšanas līdzvērtība”.

To pašu var attiecināt uz vienu savstarpējo funkciju apzīmējumu gala un bezgalīgi attālos punktos:
.
Šeit par galapunktiem
; ;
.
Be-yakі okі okolitsі neskіchenno vіddalenih punktiņi є caurdurt:
; ; .

Starpfunkciju beigu punktos

Ar loģisko simbolu palīdzību starpfunkciju apzīmējuma augstprātības iemeslu var uzrakstīt šādi:
.

Vienpusējs starp.
Kreisā robeža punktos (kreisā robeža):
.
Robežas tiesības punktos (labā robeža):
.
Mezhі levoruch i pravoruch bieži apzīmēja šādi:
; .

Starpfunkciju beigas bezgalīgi attālos punktos

Tāpat robežas tiek noteiktas bezgalīgi attālos punktos.
.
.
.

Bezgalīgas starpfunkcijas

Starp dziedošajām zīmēm var ieviest arī nekonsekventu apzīmējumu, kas vienāds ar:
.
.

Dominance un teorēmas starp funkcijām

Turklāt mēs atzīmējam, ka šīs funkcijas ir piešķirtas punkcijai pie punkta, vai nu pēc gala skaitļa, vai ar vienu no simboliem: . Arī jūs varat būt vienpusējas robežas punkts, lai māte izskatījās abo. Apkaime ir divpusēja abpusējai robežai, bet vienpusēja - vienpusējai.

Galvenās pilnvaras

Kāda ir funkcijas f vērtība (x) mainiet (vai padariet to nenozīmīgu) pie gala skaitļa punktu x 1, x 2, x 3, ... x n, tad izmaiņas nekādā veidā nav saistītas ar starpfunkcijas vērtību pietiekamā punktā x 0 .

Ja ir skaidra robeža, tad ir caurdurta punkta x nomale 0 , kurai funkcijai f (x) iežogota:
.

Lai funkcijai varētu būt punkts x 0 robežas beigas, vіdmіnna vіd nulle:
.
Tad jebkuram ciparam c intervāls tiek caurdurts ap punktu x 0 priekš kam,
, jakšo;
jakscho.

Jakščo, uz dejakom izdurtas ap punkta perifēriju, - ātri, tad.

Kā noteikt apmaļu galu un uz deaka izdurt punkta x nomali 0
,
tad.

Jakščo, un faktiskajā punkta nomalē
,
tad.
Zokrema, piemēram, deyakіy nomalē punktu
,
tad yakscho, tad i;
jakščo, tad es.

Yakshcho uz deyakomu caurdurts ap punktu x 0 :
,
un іsnuyat kintsі (vai nedziedāt zīmi) ir vienāds starp:
, tad
.

Pierādiet galvenās spējas, kas atvestas malā
"Pamata jauda starp funkcijām".

Ļaujiet funkcijām piešķirt faktiskajam caurdurtam ap punktu. Es neinteresēšu:
ka .
І not hai C ir konstants, tas ir dots skaitlis. Todi
;
;
;
jakscho.

Jakšo kaut ko.

Pierādiet aritmētiskos spēkus, kas novirzīti uz sāniem
"Aritmētiskā autoritāte starp funkcijām".

Kritēriji Koshі іsnuvannya mezhі funkії

Teorēma
Lai funkcija tiktu piešķirta deakim, kas caurdurts tuvu gala punktam vai bezgalīgi attālumā x 0 , mazs šajā robežas punktā, nepieciešams un pietiekams, neatkarīgi no ε > 0 іsnuvalа tāds caurdurts punkta x nomalē 0 , Scho par jebkuriem punktiem un z tsієї nomalē, vykonuvalsya nerіvnіst:
.

Starp locīšanas funkcijām

Teorēma par locīšanas funkcijas robežu
Ļaujiet funkcijai pārvietoties starp un parādīt caurdurtās punkta nomales punkta caurdurtajā nomalē. Lai funkcija tiktu piešķirta šai apkaimē un maijs tās robežai.
Šeit - kіntsі chi neskіchenno vіddalenі punkti: . Apkaimes, kas ir redzamas starp tām, var būt gan divpusējas, gan vienpusējas.
Todі іsnuє starp salokāmām funkcijām un vіn dorіvnyuє:
.

Ar teorēmu par saliekamas funkcijas robežu pietiek tādā gadījumā, ja funkcija nav piešķirta punktam vai tai var būt vērtība, tā neatrodas robežā. Lai pārbaudītu teorēmu, ir jāizmanto punkcija ap punktu , de bezjēdzīga funkcijas vērtība, lai nepārdurtu punktu:
.

Ja funkcija kādā punktā ir bez pārtraukuma, tad zīmi starp var iestrēgt pirms nepārtrauktās funkcijas argumenta:
.
Turklāt tika ierosināta teorēma, kas izrādīsies dzīvotspējīga.

Teorēma par robežu starp nepārtraucamu funkciju un funkciju
Ļaujiet man zināt starp funkcijām g (x) kā x → x 0 , es uzvarēju dоrіvnyuє t 0 :
.
Šeit ir punkts x 0 jūs varat būt kіntsevoi chi neskaidri vіddalenou: .
І ļauj funkcijai f (t) nepārtraukti punktā t 0 .
Todі іsnuє starp locīšanas funkcijām f (g(x)), i vіn dоvnіuє f (t0):
.

Pierādīt teorēmas, kas norādītas uz sāniem
"Starp un nepārtrauktas locīšanas funkcijas".

Bezgala mazas un bezgala lieliskas funkcijas

Bezgalīgi mazas funkcijas

Pieraksts
Funkciju sauc par bezgalīgi mazu pie , Tātad
.

Suma, mazumtirdzniecība un TV beigu skaits bezgalīgi mazu funkciju pie є bezgalīgi maza funkcija pie .

Papildus funkcija, mainīta uz deyakomu caurdurt punkta nomalē, uz bezgalīgi maza pie є bezgalīgi maza funkcija pie.

Lai funkcija starp beigām būtu maza, tā ir nepieciešama un pietiekama, tātad
,
bezgalīgi maza funkcija .

"Bezgalīgi mazu funkciju spēks".

Bezgala lieliskas funkcijas

Pieraksts
Funkciju sauc par bezgalīgi lielisku, kad
.

Funkciju summa vai starpība, uz deakim tie caurdur punktus ap punktu , un bezgalīgi lieliskā funkcija pie є bezgalīgi lieliskā funkcija pie .

Ja funkcija ir nepielūdzami liela pie , un funkcija ir ieskauta deacom punkcijā ap punktu , tad
.

Kā funkcija uz deka tie izurbās ap punktiem, apmierinot nelīdzenumus:
,
un funkcija ir bezgalīgi maza:
, i (uz deakim, kas caurdurts ap punktu ), tad
.

Pierādiet rakstīšanas spēku filiālē
"Bezgala lielu funkciju spēks".

Saikne starp bezgalīgi lieliskām un bezgalīgi mazām funkcijām

No diviem frontālajiem spēkiem ir dzirdama saikne starp bezgalīgi lielām un bezgalīgi mazām funkcijām.

Ja funkcija ir bezgalīgi liela pie , tad funkcija ir bezgalīgi maza pie .

Ja funkcija ir bezgalīgi maza , i , tad funkcija ir bezgalīgi liela .

Saikni starp bezgalīgi mazo un bezgala lielo funkciju var izteikt ar simbolisku secību:
, .

Tā kā funkcijai ir bezgalīgi maza zīme pie , tāpēc tā ir pozitīva (vai negatīva) šādā punkcijā ap punktu , tad šo faktu var izteikt šādi:
.
Tā kā funkcija pati par sevi ir bezgalīgi liela, tai var būt dziedāšanas zīme pie , tad rakstiet:
.

To pašu simbolisko saikni starp bezgala mazām un bezgala lieliskām funkcijām var papildināt ar šādu rakstību:
, ,
, .

Sānos var atrast papildu formulas, kas saista neatbilstības simbolus
"Neskaidri tā spēka punktu attālumā".

Starp monotoniskām funkcijām

Pieraksts
Tiek izsaukta funkcija, kas piešķirta reālo skaitļu reālajam reizinātājam X stingri augošs kā visiem tādiem, ka nerivnist ir fiksēts:
.
Acīmredzot, priekš suvoro norimst funkcijas
.
Priekš dārgi:
.
Priekš neaugšana:
.

Tas izklausās pēc funkcijas, ka tas stingri aug, tas ir arī neiznīcināms. Stingri trūdoša funkcija ir arī neaugšana.

Funkcija tiek izsaukta vienmuļš, it kā netiks pazemināts, vai neaug.

Teorēma
Lai funkcija nemainās ar intervāliem, de.
Turpat Jakšto ieskauj zvērs ar numuru M: Jakščo tad nav zvēru ieskauts.
Jakščo apakšā robežojas ar skaitli m: Ja tas nav apmales no apakšas, tad.

Ja punkti a un b ir neskaidri atstati, tad zimes zem zimem starp atrodas uz robežas, sho.
Šo teorēmu var formulēt kompaktāk.

Lai funkcija nemainās ar intervāliem, de. Pēc tam punktos a un b nosakiet vienpusējas robežas:
;
.

Ir līdzīga teorēma funkcijai, kas neaug.

Lai funkcija nepalielinās uz intervāla, de. Todі іsnuyut vienpusējs interі:
;
.

Teorēmas pierādījums tika pievienots malā
"Starp monotoniskām funkcijām".

Norādītās funkcijas

funkcija y=f (x) likumu (noteikumu) sauc, zgіdno z yakim, ādas elementu x reizinātāju X liek viena un tikai viena elementa y reizinātāja Y formā.

Elements x ∈ X nosaukums funkcijas arguments vai neatkarīga mana.
elements y ∈ Y nosaukums funkciju vērtības vai papuvē.

Bezpersoniskais X tiek saukts piešķirtās funkcijas apgabals.
Anonīmie elementi y ∈ Y, yakі var iepriekš konfigurēt reizinātāju X, ko sauc apgabala vai bezpersoniskas funkcijas vērtība.

Funkcija tiek izsaukta bārkstis ar zvēru (no apakšas) yaksho іsnuє tāds skaitlis M
.
Tiek izsaukta ciparu funkcija obmezhenoyu yaksho іsnuє tāds numurs M , scho visiem :
.

Augšējā puse vai precīzs augšējais kordons Faktiski funkcijas sauc par mazāko no skaitļiem, kas ieskauj zvēra vērtības laukumu. Tas ir skaitlis s, kuram visiem un jebkam ir šāds arguments, kura funkcijas vērtība tiek pārnesta s′:.
Funkcijas augšējo robežu var definēt šādi:
.

Vidpovidno apakšējā seja vai precīzs apakšējais kordons Faktiski funkcijas nosauc lielāko no skaitļiem, kas ieskauj apgabalu ar tālāk norādīto vērtību. Šādam skaitlim i , jebkuram visiem i par būt - jebkuram ir tāds arguments , kura funkcijas vērtība ir mazāka par i : .
Funkcijas apakšējo robežu var definēt šādi:
.

Vikoristanas literatūra:
L.D. Kudrjavci. Matemātiskās analīzes kurss. 1. sējums. Maskava, 2003. g.
CM. Mikilskis. Matemātiskās analīzes kurss. 1. sējums. Maskava, 1983. gads.