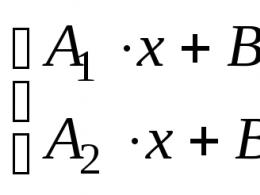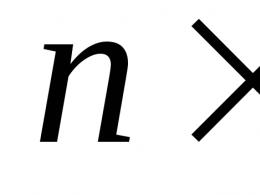Город на підвіконні

Знаходження прямого перетину площин. Пряма, задана перетином двох площин. Рівняння прямої, що проходить через дві дані точки

Пряма в просторі може бути визначена як лінія перетину двох непаралельних площин і, тобто як безліч точок, що задовольняють системі двох лінійних рівнянь

(V.5)

Справедливе і зворотне твердження: система двох незалежних лінійних рівнянь виду (V.5) визначає пряму як лінію перетину площин (якщо вони паралельні). Рівняння системи (V.5) називаються загальним рівняннямпрямий у просторі
.

ПрикладV.12 . Скласти канонічне рівняння прямої, заданої загальними рівняннями площин

Рішення. Щоб написати канонічне рівняння прямої або, що саме, рівняння прямої, що проходить через дві дані точки, потрібно знайти координати будь-яких двох точок прямої. Ними можуть бути точки перетину прямої з якими-небудь двома координатними площинами, наприклад Oyzі Oxz.

Точка перетину пряма з площиною Oyzмає абсцису
. Тому, вважаючи в даній системі рівнянь
, Отримаємо систему з двома змінними:

Її вирішення
,
разом з
визначає точку
шуканий прямий. Вважаючи в даній системі рівнянь
, отримаємо систему

рішення якої
,
разом з
визначає точку
перетину прямої з площиною Oxz.

Тепер запишемо рівняння прямої, що проходить через крапки
і
:
або
, де
буде напрямним вектором цієї прямої.

ПрикладV.13. Пряма задана канонічним рівнянням
. Скласти загальне рівняння цієї прямої.

Рішення.Канонічне рівняння прямої можна записати у вигляді системи двох незалежних рівнянь:



Отримали загальне рівняння прямої, яка тепер задана перетином двох площин, одна з яких
паралельна осі Oz (
), а інша
- Осі Оу (
).

Цю пряму можна у вигляді лінії перетину двох інших площин, записавши її канонічне рівняння у вигляді іншої пари незалежних рівнянь:



Зауваження . Одна і та ж пряма може бути задана різними системами двох лінійних рівнянь (тобто перетином різних площин, тому що через одну пряму можна провести безліч площин), а також різними канонічними рівняннями (залежно від вибору точки на прямій та її напрямного вектора) .

Ненульовий вектор, паралельний прямій лінії, називатимемо її напрямним вектором .

Нехай у тривимірному просторі задана пряма l, що проходить через точку
, та її напрямний вектор
.

Будь-який вектор
, де
, що лежить на прямий, коліна з вектором тому їх координати пропорційні, тобто

. (V.6)

Це рівняння називається канонічним рівнянням прямої. В окремому випадку, коли ﻉ є площина, отримуємо рівняння прямої на площині

. (V.7)

ПрикладV.14. Знайти рівняння прямої, що проходить через дві точки
,
.

де
,
,
.

Зручно рівняння (V.6) записати у параметричній формі. Оскільки координати напрямних векторів паралельних прямих пропорційні, то вважаючи

де t - Параметр,
.

Відстань від точки до прямої

Розглянь двовимірний евклідовий простір з декартовою системою координат. Нехай точка
ﻉ та lﻉ. Знайдемо відстань від цієї точки до прямої. Покладемо
, і пряма lзадається рівнянням
(Рис.V.8).

Відстань
, вектор
, де
– нормальний вектор прямий l,
і - Колінеарні, тому їх координати пропорційні, тобто
, отже,
,
.

Звідси
або помножуючи ці рівняння на Aі Bвідповідно і складаючи їх, знаходимо
, звідси

(V.8)

визначає відстань від точки
до прямої
.

ПрикладV.15. Знайти рівняння прямої, що проходить через точку
перпендикулярно до прямої l:
і знайти відстань від
до прямої l.

З рис. V.8 маємо
, а нормальний вектор прямий l
. З умови перпендикулярності маємо

Так як
, то

. (V.9)

Це і є рівняння прямої, яка проходить через точку
,перпендикулярно до прямої
.

Нехай маємо рівняння прямої (V.9), що проходить через точку
, перпендикулярна до прямої l:
. Знайдемо відстань від точки
до прямої l, використовуючи формулу (V.8)

Для знаходження потрібної відстані достатньо знайти рівняння прямої, що проходить через дві точки
і точку
, що лежить на прямій підставі перпендикуляра. Нехай
тоді

Так як
, а вектор
, то

. (V.11)

Оскільки точка
лежить на прямий l, то маємо ще одну рівність
або

Наведемо систему до вигляду, зручного для застосування методу Крамера

Її рішення має вигляд

. (V.12)

Підставляючи (V.12) (V.10), отримуємо вихідну відстань.

ПрикладV.16. У двомірному просторі задана точка
та пряма
. Знайти відстань від точки
до прямої; записати рівняння прямої, яка проходить через точку
перпендикулярно заданій прямій і знайти відстань від точки
до основи перпендикуляра до вихідної прямої.

За формулою (V.8) маємо

Рівняння прямої, що містить перпендикуляр, знайдемо як пряму, що проходить через дві точки
і
, скориставшись формулою (V.11) Так як
, то, з урахуванням того, що
, а
, маємо

Для знаходження координат
маємо систему з урахуванням того, що точка
лежить на вихідній прямій

Отже,
,
, Звідси.

Розглянемо тривимірне евклідове простір ﻉ. Нехай точка
ﻉ та площину ﻉ. Знайдемо відстань від цієї точки
до площини, заданої рівнянням (рис.V.9).

Аналогічно двомірному простору маємо
та вектор
, а, звідси

. (V.13)

Рівняння прямої, що містить перпендикуляр до площини , запишемо як рівняння прямої, що проходить через дві точки
і
, що лежить у площині:

. (V.14)

Для знаходження координат точки
до двох будь-яких рівностей формули (V.14) додамо рівняння

Вирішуючи систему трьох рівнянь (V.14), (V.15), знайдемо ,,– координати точки
. Тоді рівняння перпендикуляра запишеться як

Для знаходження відстані від точки
до площини замість формулою (V.13) скористаємося

У задачі необхідно знайти лінію перетину двох площин і визначити натуральну величину однієї з нихметодом плоскопаралельного переміщення.

Для вирішення такої класичної задачі з накреслювальної геометрії необхідно знати наступний теоретичний матеріал:

- Нанесення проекцій точок простору на комплексне креслення за заданими координатами;

- способи завдання площини на комплексному кресленні, площині загального та приватного становища;

- Головні лінії площини;

- Визначення точки перетину прямої лінії з площиною (знаходження «точки зустрічі»);

метод плоскопаралельного переміщення для визначення натуральної величини плоскої фігури;

- Визначення видимості на кресленні прямих ліній і площин за допомогою конкуруючих точок.

Порядок розв'язання Завдання

1. Згідно з варіантом Завдання за координатами точок наносимо на комплексне креслення дві площини, задані у вигляді трикутників. ABC(A', B', C'; A, B, C) та DKE(D', K', E'; D, K, Е) ( рис.1.1).

Рис.1.1

2 . Для знаходження лінії перетину скористаємося методом проекції площини. Суть його в тому, що береться одна сторона (лінія) першої площини (трикутника) і полягає в проекції площини. Визначається точка перетину цієї лінії із площиною другого трикутника. Повторивши це завдання ще раз, але для прямої другого трикутника та площини першого трикутника, визначимо другу точку перетину. Оскільки отримані точки одночасно належать обом площинам, вони повинні перебувати на лінії перетину цих площин. З'єднавши ці точки прямий, матимемо лінію перетину площин.

3. Завдання вирішується так:

а)укладаємо в проеціюючу площину Ф(Ф’)бік AB(A’ B’) першого трикутника у фронтальній площині проекцій V. Зазначаємо точки перетину проєкуючої площини зі сторонами DKі DEдругого трикутника, отримуючи точки 1(1') та 2 (2'). Переносимо їх лініями зв'язку на горизонтальну площину проекцій Hна відповідні сторони трикутника, точка 1 (1) на стороні DEі крапка 2(2) на стороні DK.

Рис.1.2

б)з'єднавши проекції точок 1 та 2, матимемо проекцію проєкуючої площини Ф. Тоді точка перетину прямої АВз площиною трикутника DKE визначиться (згідно з правилом) разом перетину проекції проекції площини 1-2 та однойменної проекції прямої AB. Таким чином, отримали горизонтальну проекцію першої точки перетину площин – M, За якою визначаємо (проеціюємо по лініях зв'язку) її фронтальну проекцію - M’ на прямий A’ B’ (рис.1.2.а);

в)аналогічним шляхом знаходимо другу точку. Укладаємо в проеціюючу площину Г(Г)бік другого трикутника DK(DK) . Зазначаємо точки перетину проєкуючої площини зі сторонами першого трикутника ACіBCу горизонтальній проекції, одержуючи проекції точок 3 та 4. Проектуємо їх на відповідні сторони у фронтальній площині, отримуємо 3’ та 4’. З'єднавши їх прямий, маємо проекцію площини, що проеціює. Тоді друга точка перетину площин буде в місці перетину лінії 3’-4’ зі стороною трикутника D’ K’ , яку укладали в проеціюючу площину. Таким чином, отримали фронтальну проекцію другої точки перетину – N’ , по лінії зв'язку знаходимо горизонтальну проекцію - N (рис.1.2.б).

г)з'єднавши отримані точки MN(MN) і (M’ N’) на горизонтальній та фронтальній площинах, маємо лінію перетину заданих площин.

4. За допомогою конкуруючих точок визначаємо видимість площин. Візьмемо пару конкуруючих точок, наприклад, 1’=5’ у передній проекції. Спроектуємо їх на відповідні сторони у горизонтальну площину, отримаємо 1 та 5. Бачимо, що точка 1 , що лежить на стороні DЕмає велику координату до осі xніж точка 5 , що лежить на стороні AВ. Отже, згідно з правилом, більшої координати, точка 1 та сторона трикутника D’ЄУ фронтальній площині будуть видимі. Таким чином, визначається видимість кожної сторони трикутника в горизонтальній та фронтальній площинах. Видимі лінії на кресленнях проводяться суцільною контурною лінією, а чи не видимі — штриховою лінією. Нагадаємо, що в точках перетину площин ( M— N іM’- N’ ) відбуватиметься зміна видимості.

Рис.1.3

Ріс.1.4 .

На епюрі додатково показано визначення видимості у горизонтальній площині з використанням конкуруючих точок. 3 і 6 на прямих DKі АВ.

5. Методом плоскопаралельного переміщення визначаємо натуральну величину площини трикутника ABC, для чого:

а)у зазначеній площині через точку С(С)проводимо фронталь C— F(С-FіC’- F’) ;

б)на вільному полі креслення у горизонтальній проекції беремо (зазначаємо) довільну точку З 1, вважаючи, що це одна з вершин трикутника (конкретно вершина C). З неї відновлюємо перпендикуляр до передньої площини (через вісь х);

Рис.1.5

в)плоскопаралельним переміщенням переводимо горизонтальну проекцію трикутника ABC, у нове положення A 1 B 1 C 1 таким чином, щоб у фронтальній проекції він зайняв проецірующее положення (перетворився на пряму лінію). Для цього: на перпендикулярі від точки З 1, відкладаємо фронтальну проекцію горизонталі C 1 — F 1 (довжина l CF) отримуємо точку F 1 . Розчином циркулю з точки F 1величиною F-Aробимо дугове засічення, а з точки C 1 - Засікання величиною CAтоді в перетині дугових ліній отримуємо точку A 1 (Друга вершина трикутника);

- аналогічно отримуємо точку B 1 (З точки C 1 робимо засічку завбільшки C— B(57мм), а з точки F 1 величиною F— B(90мм). Зауважимо, що при правильному вирішенні три точки A 1 F’ 1 і B’ 1 повинні лежати на одній прямій (сторона трикутника A 1 — B 1 ) дві інші сторони З 1 — A 1 і C 1 — B 1 виходять шляхом з'єднання їх вершин;

г)з методу обертання випливає, що при переміщенні або обертанні точки в якійсь площині проекцій - на сполученій площині проекція цієї точки повинна рухатися прямою лінією, в нашому конкретному випадку по прямій паралельній осі х. Тоді проводимо з точок A’ B’ C’ фронтальної проекції ці прямі (їх називають площинами обертання точок), та якщо з фронтальних проекцій переміщених точок A 1 В 1C 1 відновимо перпендикуляри (лінії зв'язку) ( рис.1.6).

Рис.1.6

Перетин зазначених ліній з відповідними перпендикулярами дає нові положення фронтальної проекції трикутника ABC, конкретно A’ 1 В 1C’ 1 який має стати проектуючим (прямою лінією), оскільки горизонталь h 1 ми провели перпендикулярно фронтальній площині проекцій ( рис.1.6);

5) тоді для отримання натуральної величини трикутника досить його фронтальну проекцію розгорнути паралельно з горизонтальною площиною. Розворот здійснюємо за допомогою циркуля через точку А’ 1, рахуючи її як центр обертання, ставимо трикутник A’ 1 В 1C’ 1 паралельно осі х, отримуємо A’ 2 В 2C’ 2 . Як було сказано вище, при обертанні точки, на сполученій (тепер на горизонтальній) проекції вони рухаються по прямих паралельних осях х. Опускаючи перпендикуляри (лінії зв'язку) з передніх проекцій точок A’ 2 В 2C’ 2 перетину їх з відповідними лініями знаходимо горизонтальну проекцію трикутника ABC (A 2 В 2C 2 ) в натуральну величину ( рис.1.7).

Рис. 1.7

У мене є всі готові розв'язання задач із такими координатами, купити можна

Ціна 55 руб, креслення з накреслювальної геометрії з книги Фролова Ви легко можете завантажити одразу після оплати або я надішлю Вам на пошту. Вони знаходяться в ZIP архіві у різних форматах:
*.jpg – звичайний кольоровий малюнок креслення масштабу 1 до 1 хорошому дозволі 300 dpi;
*.cdw – формат програми Компас 12 та вище або версії LT;
*.dwg та.dxf — формат програми AUTOCAD; nanoCAD;

Розділ: Накреслювальна геометрія /

Канонічні рівняння прямої

Постановка задачі. Знайти канонічні рівняння прямої, заданої як лінія перетину двох площин (загальними рівняннями)

План розв'язання. Канонічні рівняння прямої з напрямним вектором , що проходить через цю точку , мають вигляд

. (1)

Тому, щоб написати канонічні рівняння прямої, необхідно знайти її напрямний вектор і якусь точку на прямій.

1. Оскільки пряма належить одночасно обом площинам, її напрямний вектор ортогонален нормальним векторам обох площин, тобто. згідно з визначенням векторного твору, маємо

. (2)

2. Вибираємо якусь точку на прямій. Оскільки напрямний вектор прямий паралельний хоча б однієї з координатних площин, то пряма перетинає цю координатну площину. Отже, як точка на прямій може бути взята точка її перетину з цією координатною площиною.

3. Підставляємо знайдені координати напрямного вектора та точки в канонічні рівняння прямої (1).

Зауваження. Якщо векторний добуток (2) дорівнює нулю, то площини не перетинаються (паралельні) і записати канонічні рівняння прямої неможливо.

Завдання 12.Написати канонічні рівняння прямої.

Канонічні рівняння прямої:

де – координати будь-якої точки прямої, – її напрямний вектор.

Знайдемо якусь точку прямої . Нехай тоді

Отже, – координати точки, що належить прямій.

Завдання на перетин площин через свою важливість носить у ряду авторів найменування «позиційне завдання № 2».

Зі стереометрії відомо, що лінією перетину двох площин служить пряма. У попередніх попередніх завданнях, де йшлося про окремі випадки перетину площин, ми виходили з цього визначення.

Як відомо, щоб побудувати ту чи іншу пряму, у найпростішому випадку потрібно відшукати дві точки, що належать до цієї прямої. У разі завдання площини слідами як ці дві точки виступають точки перетину однойменних слідів площин, що перетинаються.

Приклади для самостійної роботи

Вправа 5.1

Побудувати лінії перетину площин, заданих слідами (мал. 72):

а) горизонтально проецірующій I і фронтально проецірующій А;
б) горизонтально проецирующей Z та площині загального положення Q;
в) двох площин загального становища I та 0.

Рис. 72

На рис. 73 наведено відповіді на цю вправу.

Для випадків завдання площин локальними плоскими фігурами доречне використання принаймні двох різних способів вирішення.

Рис. 73

Перший шлях вирішення -використання триступеневого алгоритму знаходження точки зустрічі прямого загального стану з площиною загального положення. Для знаходження лінії перетину двох трикутників один із трикутників залишають без зміни, а другий подумки розчленовують на окремі відрізки, представляючи їх як прямі загального положення. Спочатку знаходять точку перетину однієї з прямих загального стану з площиною трикутника. Потім знаходять ще одну відсутню точку, що належить шуканої лінії. Це робиться аналогічним шляхом, повторюючи всю описану послідовність дій.

Вправа 5.2

За заданими координатами вершин двох трикутників ЛОМі DEKпобудувати епюр останніх та знайти лінію їх перетину. Вказати видимість елементів обох трикутників на епюрі: А(0, 9, 2); ?(10, 1, 16); З (23, 14, 9); D(3, 17, 18); ? (22, 11, 17); ? (12,0, 2). Для знаходження ліній перетину трикутників рекомендується спочатку знайти точку зустрічі прямої KDз трикутником АВС,а потім точку зустрічі прямої СВз трикутником EDK.

Загальний вигляд отриманого епюра наведено на рис. 74.

Другий шлях вирішення -використання двох допоміжних сіючих площин рівня.

Задані плоскі фігури, що перетинаються, слід двічі перетнути допоміжними площинами рівня (одноіменними або різноіменними - байдуже), наприклад двома горизонтальними площинами рівня.

Неважко зрозуміти, що одноразове розтин дозволяє знайти дві перетинаються прямі h lі І 2 ,дають одну точку А,що належить шуканій лінії перетину (рис. 75). Проводячи ще одну аналогічну допоміжну площину на певній відстані

Рис. 74

Рис. 75

від першої, отримують аналогічну побудову та ще одну точку. З'єднуючи однойменні проекції двох отриманих точок, знаходять лінію перетину двох площин.

Вправа 5.3

За заданими координатами точок двох трикутних фігур побудувати епюр останніх, на якому побудувати з використанням допоміжних площин лінію перетину трикутників. Вказати видимість елементів обох трикутників на епюрі:

до АВС. А(16, 5, 17); Я (10, 19,

A DEF: D (24, 12, 14); ? (4, 18,

Загальний вигляд вирішеної задачі зображено на рис. 76.

Вправа 5.4

Для закріплення навичок знаходження лінії перетину двох площин наводиться задача, розв'язання якої дається в динаміці побудов відповідно до ступенів алгоритму.

Знайти лінію перетину двох площин загального положення. рис jq

ня, заданих двома трикутниками АВСі DEF,і визначити видимість їхнього взаємопроникнення (рис. 77).

Рішення прикладу зводиться до пошуку точок перетину сторонами (прямими) А АВСз площиною загального положення, заданою A DEF.Алгоритм розв'язання цього прикладу відомий.

Укладаємо бік (прямий) АС ЬЛВСу допоміжну фронтально проецірующій площину т _1_ П 2 (рис. 78).

Фронтальний слід цієї допоміжної площини перетинає проекції сторін D 2 E 2 глЕ 2 - 1 2 D 2 F 2пт 2 = 2 2 у точках 1 2 та 2 2 . Проекційні лінії зв'язку дозволяють на горизонтальній площині проекцій визначити лінію перетину (1 !~2 2) = n A D X E X F ( .Тоді точка До 1та її проекція До 2визначають точку перетину прямої АСз A DEF.

Повторюємо алгоритм знаходження точки перетину сторони А АВСпрямий НДз ADEF. Укладаємо ПС у допоміжну фронтально проецірующую площину р _L П 2 (рис. 79).

Знаходимо проекції точок 3 та 4 і на горизонтальній площині проекцій визначаємо проекцію точки перетину прямої У 1 З [з лінією перетину (3,-4,):

Проекційна лінія зв'язку дозволяє знайти її фронтальну проекцію крапку М2.

З'єднуємо знайдені точки Кі Мізнаходимо лінію перетину двох площин загального положення A ABC n A DEF=АЖ (рис. 80).

Видимість сторін ААВСщодо ADEFвизначається за допомогою конкуруючих точок. Спочатку визначаємо видимість геометричних постатей на площині проекцій П 2 . Для цього через конкуруючі точки 5 та 6 (5 2 = 6 2) проводимо проекційну лінію зв'язку, перпендикулярну до осі проекцій х п(Рис. 81).

По горизонтальних проекціях 5 Уі 6 { точок 5 і 6, в яких лінія проекційного зв'язку відповідно перетинає прямі, що схрещуються АС 4 DF,з'ясовується, що точка 6 більш віддалена від площини проекцій П 2 ніж точка 5. Тому точка 6 і пряма DF,якій вона належить, видно щодо площини проекцій П 2 . Звідси випливає, що відрізок (До 2 -6 2)буде невидимим. Аналогічно визначаємо видимість сторін А ЛОМта A DEF - НДі DF,тобто. відрізок (Ж 2 -8 2) буде невидимим.

Видимість ААВСі ADEFщодо площини проекцій П j встановлюється аналогічно. Для визначення видимості прямих, що схрещуються АС*DFі НД ±DFщодо площини проекцій П] через конкуруючі точки 9 1 = 10 1 та 11 1 = 12 1 проводимо проекційні лінії зв'язку перпендикулярно х п.По фронтальним проекціям цих конкуруючих точок встановлюємо, що проекції точок 10 2 і 12 більш віддалені від площини проекцій П ( .Отже, відрізки (А^-ЮД і (М р 2 1)будуть невидимими. Звідси видимість ААВСі ADEFнаочно представлена на рис. 82.

Канонічними рівняннями прямої в просторі називаються рівняння, що визначають пряму, що проходить через задану точку колінеарно спрямовуючому вектору.

Нехай дана точка та напрямний вектор. Довільна точка лежить на прямій lтільки в тому випадку, якщо вектори та колінеарні, тобто для них виконується умова:

Наведені вище рівняння є канонічні рівняння прямої.

Числа m , nі pє проекціями напрямного вектора координатні осі. Оскільки вектор ненульовий, всі числа m , nі pне можуть одночасно дорівнювати нулю. Але один або два з них можуть виявитися рівними нулю. В аналітичній геометрії допускається, наприклад, такий запис:

яка означає, що проекції вектора на осі Ойі Ozрівні нулю. Тому і вектор, і пряма, задана канонічними рівняннями, перпендикулярні до осей. Ойі Oz, тобто площині yOz .

приклад 1.Скласти рівняння прямої у просторі, перпендикулярній площині і проходить через точку перетину цієї площини з віссю Oz .

Рішення. Знайдемо точку перетину даної площини з віссю Oz. Оскільки будь-яка точка, що лежить на осі Ozмає координати , то, вважаючи в заданому рівнянні площини x = y = 0 , отримаємо 4 z- 8 = 0 або z= 2 . Отже, точка перетину даної площини з віссю Ozмає координати (0; 0; 2). Оскільки пряма перпендикулярна площині, вона паралельна вектору її нормалі . Тому напрямним вектором прямий може бути вектор нормалі заданої поверхні.

Тепер запишемо шукані рівняння прямої, що проходить через точку A= (0; 0; 2) у напрямку вектора:

Рівняння прямої, що проходить через дві дані точки

Пряма може бути задана двома точками, що на ній лежать і У цьому випадку напрямним вектором прямий може бути вектор . Тоді канонічні рівняння прямий набудуть вигляду

Наведені вище рівняння визначають пряму, що проходить через дві задані точки.

приклад 2.Скласти рівняння прямої в просторі, що проходить через точки і .

Рішення. Запишемо шукані рівняння прямої у вигляді, наведеному вище в теоретичній довідці:

Оскільки , то пряма перпендикулярна осі Ой .

Пряма як лінія перетину площин

Пряма у просторі може бути визначена як лінія перетину двох непаралельних площин і, тобто як безліч точок, що задовольняють системі двох лінійних рівнянь

Рівняння системи називаються загальними рівняннями прямої в просторі.

Приклад 3.Скласти канонічні рівняння прямої у просторі, заданій загальними рівняннями

Рішення. Щоб написати канонічні рівняння прямої або, що те саме, рівняння прямої, що проходить через дві дані точки, потрібно знайти координати будь-яких двох точок прямої. Ними можуть бути точки перетину прямої з якими-небудь двома координатними площинами, наприклад yOzі xOz .

Точка перетину пряма з площиною yOzмає абсцису x= 0. Тому, вважаючи в даній системі рівнянь x= 0 отримаємо систему з двома змінними: