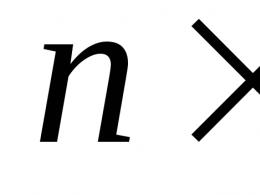Рівновість тіла за наявності тертя ковзання. Рівновість твердого тіла за наявності тертя Рівновість тіла за наявності тертя ковзання

Модуль 2 складається з двох лекцій у яких вивчаються такі питання:

1. Рівновість системи тел.
2. Розрахунок ферм.
3. Концепція ферми.
4. Аналітичний розрахунок плоских ферм.
5. Графічний розрахунок плоских ферм.
6. Тертя.
7. Закони тертя ковзання.
8. Реакції шорстких зв'язків.
9. Кут тертя.
10. Рівноваги за наявності тертя.
11. Тертя кочення та обертання.
12. Момент сили щодо центру як вектор.
13. Час пари сил як вектор.
14. Момент сили щодо осі.
15. Залежність між моментами сили щодо центру та щодо осі.
16. Приведення просторової системи зусиль до даного центру.
17. Умови рівноваги довільної просторової системи сил.
18. Завдання на рівновагу тіла під впливом просторової системи сил.
19. Центр важкості твердого тіла.
20. Координати центрів тяжкості однорідних тіл.
21. Центри тяжкості деяких однорідних тіл.

Вивчення даних питань необхідно надалі вивчення динаміки руху тіл з урахуванням тертя ковзання і тертя кочення, динаміки руху центру мас механічної системи, кінетичних моментів, на вирішення завдань у дисципліні «Опір матеріалів».

Рівновість систем тел.

Статичний розрахунок інженерних споруд у багатьох випадках зводиться до розгляду умов рівноваги конструкції із системи тіл, з'єднаних якими-небудь зв'язками. Зв'язки, що з'єднують частини даної конструкції, називатимемо внутрішніми, на відміну від зовнішніх зв'язків, що скріплюють конструкцію з тілами, які до неї не входять (наприклад, з опорами).

Якщо після відкидання зовнішніх зв'язків (опор) конструкція залишається жорсткою, то для неї завдання статики вирішуються як для абсолютно твердого тіла.

Однак, можуть зустрічатися такі інженерні конструкції, які після відкидання зовнішніх зв'язків не залишаються жорсткими. Прикладом такої конструкції є тришарнірна арка (рис. 22). Якщо відкинути опори А та В, то арка не буде жорсткою: її частини можуть повертатися навколо шарніру.

На підставі принципу затвердіння система сил, що діють на таку конструкцію, при рівновазі повинна задовольняти умовам рівноваги твердого тіла. Але ці умови, як вказувалося, необхідними, не будуть достатніми, тому з них не можна буде визначити всіх невідомих. Для вирішення задачі необхідно додатково розглянути рівновагу якої-небудь однієї або декількох частин конструкції.

Наприклад, складаючи умови рівноваги для сил, що діють на три шарнірну арку (див. рис. 22), ми отримаємо три рівняння з чотирма невідомими XA, YA, XB, YB. Розглянувши додатково умови рівноваги лівої (або правої) її половини, ми отримаємо ще три рівняння, що містять два нові невідомі ХC, YC, на рис. 22 не показані. Вирішуючи отриману систему шести рівнянь, знайдемо усі шість невідомих.

Інший спосіб вирішення подібних завдань полягає в тому, що конструкцію відразу розчленовують на окремі тіла та становлять умови рівноваги кожного з тіл, розглядаючи його як вільне. При цьому реакції внутрішніх зв'язків будуть рівні по модулю і протилежні у напрямку. Для конструкції з п тіл, на кожне з яких діє довільна плоска система сил, вийде таким шляхом 3n рівнянь, що дозволяють знайти Зn невідомих (за інших систем сил число рівнянь відповідно зміниться). Якщо для даної конструкції число всіх реакцій зв'язків буде більшим за кількість рівнянь, в які ці реакції входять, то конструкція буде статично невизначеною.

Розрахунок ферм.

Концепція ферми. Аналітичний розрахунок плоских ферм.

Фермою називається жорстка конструкція із прямолінійних стрижнів, з'єднаних на кінцях шарнірами. Якщо всі стрижні ферми лежать в одній площині, то ферма називається плоскою. Місця з'єднання стрижнів ферми називають вузлами. Усі зовнішні навантаження до ферми прикладаються лише у вузлах. При розрахунку ферми тертям у вузлах і вагою стрижнів (порівняно із зовнішніми навантаженнями) нехтують або розподіляють ваги стрижнів за вузлами. Тоді на кожен із стрижнів ферми діятимуть дві сили, прикладені до його кінців, які при рівновазі можуть бути спрямовані лише вздовж стрижня. Отже, можна вважати, що стрижні ферми працюють тільки на розтяг або на стиснення. Обмежимося розглядом твердих плоских ферм, без зайвих стрижнів, утворених із трикутників. У таких фермах число стрижнів k та число вузлів п пов'язані співвідношенням

Розрахунок ферми зводиться до визначення опорних реакцій та зусиль у її стрижнях.

Опорні реакції можна знайти звичайними методами статики, розглядаючи ферму як тверде тіло. Перейдемо до визначення зусиль у стрижнях.

Метод вирізування вузлів. Цим методом зручно користуватися, коли треба знайти зусилля у всіх стрижнях ферми. Він зводиться до послідовного розгляду умов рівноваги сил, які сходяться на кожному з вузлів ферми. Хід розрахунків пояснимо на конкретному прикладі.

Розглянемо зображену на рис. 2З,а ферму, утворену з однакових рівнобедрених прямокутних трикутників; сили, що діють на ферму, паралельні осі х і рівні: F1 = F2 = F3 = F = 2.

У цій фермі число вузлів n = 6, а число стрижнів k = 9. Отже співвідношення виконується і ферма є жорсткою, без зайвих стрижнів.

Складаючи рівняння рівноваги для ферми загалом, знайдемо, що реакції опор спрямовані, як показано малюнку, і чисельно рівні;

Переходимо до визначення зусиль у стрижнях.

Пронумеруємо вузли ферми римськими цифрами, а стрижні – арабськими. Шукані зусилля позначатимемо S1 (у стрижні 1), S2 (у стрижні 2) і т. д. Відріжемо подумки всі вузли разом з стрижнями, що сходяться в них від решти ферми. Дія відкинутих частин стрижнів замінимо силами, які будуть спрямовані вздовж відповідних стрижнів і чисельно рівні шуканим зусиллям S1, S2, ... Зображаємо відразу всі ці сили на малюнку, спрямовуючи їх від вузлів, тобто вважаючи всі стрижні розтягнутими (мал. 23, а, зображену картину треба уявляти для кожного вузла так, як це показано на рис.23, б для вузла III). Якщо в результаті розрахунку величина зусилля в якомусь стрижні вийде негативною, це означатиме, що даний стрижень не розтягнутий, а стиснутий. Літерних позначень для сил, що діють вздовж стрижнів, ні рис. 2З не введенням, оскільки ясно, що сили, що діють вздовж стрижня 1, чисельно рівні S1, вздовж стрижня 2 - рівні S2 і т. д.

Тепер для сил, що сходяться у кожному вузлі, складаємо послідовно рівняння рівноваги

Починаємо з вузла 1, де сходяться два стрижні, тому що з двох рівнянь рівноваги можна визначити лише два невідомі зусилля.

Складаючи рівняння рівноваги для вузла 1, отримаємо

Звідси знаходимо

Тепер, знаючи S1, переходимо до вузла ІІ. Для нього рівняння рівноваги дають

Визначивши S4, складаємо аналогічним шляхом рівняння рівноваги спочатку для вузла ІІІ, а потім для вузла ІV. З цих рівнянь знаходимо:

Нарешті, для обчислення S9 складаємо рівняння рівноваги сил, що сходяться у вузлі V проектуючи їх на вісь By. Отримаємо звідки

Друге рівняння рівноваги для вузла V та два рівняння для вузла VI можна скласти як перевірочні. Для знаходження зусиль у стрижнях ці рівняння не знадобилися, оскільки замість них було використано три рівняння рівноваги всієї ферми загалом щодо N, ХА, і YА.

Остаточні результати розрахунку можна звести до таблиці:

Як показують знаки зусиль, стрижень 5 розтягнутий, решта стрижні стиснута; стрижень 7 не навантажений (нульовий, стрижень).

Наявність у фермі нульових стрижнів, подібних до стрижня 7, виявляється відразу, тому що якщо у вузлі, не навантаженому зовнішніми силами, сходяться три стрижні, з яких два направлені вздовж однієї прямої, то зусилля в третьому стрижні дорівнює нулю. Цей результат виходить із рівняння рівноваги у проекції на вісь, перпендикулярну до згаданих двох стрижнів.

Якщо під час розрахунку зустрінеться вузол, котрого число невідомих більше двох, можна скористатися методом перерізів.

Метод перерізів (метод Ріттера). Цим методом зручно користуватися визначення зусиль в окремих стрижнях ферми, зокрема, для перевірочних розрахунків. Ідея методу полягає в тому, що ферму поділяють на дві частини перетином, що проходить через три стрижні, в яких (або в одному з яких) потрібно визначити зусилля і розглядають рівновагу однієї з цих частин. Дія відкинутої частини замінюють відповідними силами, спрямовуючи їх уздовж розрізаних стрижнів від вузлів, тобто вважаючи стрижні розтягнутими (як і методом вирізування вузлів). Потім становлять рівняння рівноваги, беручи центри моментів (чи вісь проекцій) те щоб у кожне рівняння увійшло лише одне невідоме зусилля.

Графічний розрахунок плоских ферм.

Розрахунок ферми шляхом вирізування вузлів може здійснюватися графічно. Для цього спочатку визначають опорні реакції. Потім, послідовно відсікаючи від ферми кожен із її вузлів, знаходять зусилля у стрижнях, які у цих вузлах, будуючи відповідні замкнені силові багатокутники. Усі побудови проводяться у масштабі, який має бути заздалегідь обраний. Розрахунок починають із вузла, в якому сходяться два стрижні (інакше не вдасться визначити невідомі зусилля).

Як приклад розглянемо ферму, зображену на рис. 24, а. У цьому фермі число вузлів n =6, а число стрижнів k=9. Отже, співвідношення виконується і ферма є твердою, без зайвих стрижнів. Опорні реакції R4 і R5 для ферми, що розглядається, зображуємо поряд з силами F1, F2 і F3, як відомі.

Визначення зусиль у стрижнях починаємо з розгляду стрижнів, що сходяться у вузлі I (вузли нумеруємо римськими цифрами, а стрижні – арабськими). Подумки відрізавши від цих стрижнів решту ферми, відкидаємо її дію відкинутої частини також подумки замінюємо силами S1 і S2, які повинні бути спрямовані вздовж стрижнів 1 і 2. З сили, що сходяться в вузлі I сил R5, S1 і S2 будуємо замкнутий трикутник (рис. 24). , б). Для цього зображуємо спочатку у вибраному масштабі відому силу R5, а потім проводимо через її початок і кінець прямі, паралельні стрижням 1 і 2. Таким шляхом будуть знайдені сили S1 і S2, що діють на стрижні 1 і 2. Потім розглядаємо рівновагу стрижнів, що сходяться вузлі ІІ. Дія на ці стрижні відкинутої частини ферми подумки замінюємо силами S1 ', S2 і S4, спрямованими вздовж відповідних стрижнів; при цьому сила S1 нам відома, оскільки за рівністю дії і протидії S1 = -S1. Побудувавши із сил, що сходяться у вузлі II, замкнутий трикутник (починаючи з сили S1'), знайдемо величини S3 та S4 (у даному випадку S4 = =0). Аналогічно перебувають зусилля інших стрижнях. Відповідні силові багатокутники для всіх вузлів показано на рис. 24, б. Останній багатокутник (для вузла VI) будується для перевірки, оскільки всі сили, що входять до нього, вже знайдені.

Зі побудованих багатокутників, знаючи масштаб, знаходимо величини всіх зусиль. Знак зусилля у кожному стрижні визначається наступним чином. Подумки вирізавши вузол по стрижням, що сходяться в ньому (наприклад, вузол III), прикладаємо до обрізів стрижнів знайдені сили (рис. 25); сила, спрямована від вузла (S5 на рис. 25), розтягує стрижень, а сила, спрямована до вузла (S3 і S6 на рис. 25) стискає його.

Згідно з прийнятою умовою зусиллям, що розтягують, приписуємо знак «+», а стискаючим - знак «-». У розглянутому прикладі (рис. 25) стрижні 1, 2, 3, 6, 7, 9 стиснуті, а стрижні 5, 8 розтягнуті.

Тертя.

Закони тертя ковзання.

Досвід показує, що при прагненні рухати одне тіло поверхнею іншого в площині дотику тіл виникає сила опору їх відносному ковзанню, звана силою тертя ковзання.

Виникнення тертя обумовлено, насамперед, шорсткістю поверхонь, що створює опір переміщенню, та наявністю зчеплення у притиснутих один до одного тіл. Вивчення всіх особливостей явища тертя є досить складною фізико-механічною проблемою, розгляд якої виходить за рамки курсу теоретичної механіки.

У інженерних розрахунках зазвичай виходять із низки встановлених дослідним шляхом загальних закономірностей, які з достатньої практики точністю відбивають основні особливості явища тертя. Ці закономірності, звані законами тертя ковзання при спокої, можна сформулювати так:

Сила тертя спрямована у бік, протилежний тій, куди сили, що діють, прагнуть зрушити тіло.

Статичний коефіцієнт тертя - число абстрактне; він визначається дослідним шляхом і залежить від матеріалу дотичних тіл і стану поверхонь (характер обробки, температура, вологість, мастило тощо).

1. Величина граничної сили тертя в досить широких межах не залежить від розмірів поверхонь, що стикаються при терті.

Об'єднуючи разом перший і другий закони, отримуємо, що при рівновазі сила тертя спокою (сила зчеплення) або

Реакції шорстких зв'язків. Кут тертя.

До цього часу при вирішенні завдань статики ми нехтували тертям і вважали поверхні зв'язків гладкими, які реакції спрямованими за нормалями до цих поверхонь. Реакція реального (шорсткого) зв'язку складатиметься з двох складових: з нормальної реакції N та перпендикулярної до неї сили тертя F. Отже, повна реакція R буде відхилена від нормалі до поверхні на деякий кут. При зміні сили тертя від нуля до Fпр сила R змінюватиметься від N до Rпр, а її кут з нормаллю зростатиме від нуля до деякого граничного значення φ0 (рис. 26). Найбільший кут φ0, який повна реакція шорсткого зв'язку утворює з нормаллю до поверхні, називається кутом тертя. З креслення видно, що

Оскільки , звідси знаходимо наступний зв'язок між кутом тертя та коефіцієнтом тертя:

При рівновазі повна реакція R, залежно від зсуву, може проходити де завгодно всередині кута тертя. Коли рівновага стає граничною, реакція відхиляється від нормалі на кут φ0.

Якщо до тіла, що лежить на шорсткої поверхні, додати силу Р, що утворює кут α з нормаллю (рис. 27), то тіло зрушиться тільки тоді, коли зсув зусилля Рsinα буде більшим (ми вважаємо, нехтуючи вагою тіла). Але нерівність , в якому виконується тільки при , тобто при α>φ0. Отже, жодною силою, яка утворює з нормаллю кут.

α, менший за кут тертя 0, тіло вздовж даної поверхні зрушити не можна. Цим пояснюються відомі явища заклинювання чи самогальмування тіл.

Рівноваги за наявності тертя.

Вивчення рівноваги тіл з урахуванням тертя зводиться зазвичай до розгляду граничного положення рівноваги, коли сила тертя досягає найбільшого значення . При аналітичному розв'язанні задач реакцію шорсткого зв'язку в цьому випадку зображують двома складовими N і де. Потім становлять звичайні умови рівноваги статики, підставлять у них замість величину і, вирішуючи отримані рівняння, визначають шукані величини.

Тертя кочення та обертання.

Тертям кочення називається опір, що виникає при коченні одного тіла поверхнею іншого.

Розглянемо круглий циліндричний каток радіусу R і ваги Р, що лежить на горизонтальній шорсткій площині. Прикладемо до осі катка силу Q (рис. 28 а), меншу Fпр. Тоді в точці А виникає сила тертя F, чисельно рівна Q, яка перешкоджатиме ковзанню циліндра по площині. Якщо рахувати нормальну реакцію N теж прикладеної в точці А, вона врівноважує силу Р, а сили Q і F утворюють пару, що викликає кочення циліндра. При такій схемі кочення має початися, як бачимо, під дією будь-якої, скільки завгодно малої сили Q

Справжня картина, як показує досвід, виглядає інакше. Пояснюється це тим, що фактично внаслідок деформацій тіл дотик їх відбувається вздовж деякого майданчика АВ (рис. 28, б). При дії сили Q інтенсивність тисків у краю А зменшується, а в краю В зростає. В результаті реакція N виявляється зміщеною у бік дії сили Q. Зі збільшенням Q це зсув зростає до деякої граничної величини k. Таким чином, у граничному положенні на каток діятимуть пара (Qпр, F) з моментом QпрR і пара, що врівноважує (N, Р) з моментом Nk. З рівності моментів знаходимо QпрR = Nk або

Поки що, ковзанка перебуває у спокої; при починається кочення.

Лінійна величина k, що входить у формулу, називається коефіцієнтом тертя кочення. Вимірюють величину k зазвичай сантиметрах. Значення коефіцієнта k залежить від матеріалу тіл та визначається дослідним шляхом.

Відношення k/R більшості матеріалів значно менше статичного коефіцієнта тертя f0. Цим пояснюється те, що у техніці, коли це можливо, прагнуть замінити ковзання коченням (колеса, ковзанки, кулькові підшипники тощо).

Момент сили щодо центру як вектор.

Щоб перейти до розв'язання задач статики для системи сил, як завгодно розташованих у просторі, необхідно кілька уточнити і розширити ряд введених раніше понять. Почнемо з уявлення про момент сили.

1. Зображення моменту вектор. Момент сили F щодо центру (див. рис. 29) як характеристика її обертального ефекту визначається наступними трьома елементами:

1. модулем моменту, рівним добутку модуля сили на плече, тобто Fh; 2) площиною повороту ОАВ, що проходить через лінію дії сили F та центр; 3) напрямом повороту у цій площині. Коли всі сили і центр лежать в одній площині, необхідність задавати щоразу площину повороту ОАВ відпадає, і момент можна визначати як скалярну алгебраїчну величину, що дорівнює ±Fh, де знак вказує напрямок повороту.

Але у разі сил, які довільно розташовані в просторі, площини повороту у різних сил будуть різними і повинні задаватися додатково. Положення площини в просторі можна встановити, задавши відрізок (вектор), перпендикулярний до цієї площини. Якщо одночасно модуль цього вектора вибрати рівним модулю моменту сили і домовитися спрямовувати цей вектор так, щоб його напрямок визначав напрямок повороту сили, такий вектор повністю визначить всі три елементи, що характеризують момент даної сили щодо центру Про.

Тому в загальному випадку момент mo(F) сили F щодо центру О (рис. 29) зображуватимемо прикладеним у центрі Про вектором Мо, рівним за модулем (у вибраному масштабі) добутку модуля сили F на плече h і перпендикулярним до площини ОАВ, що проходить через центр О і силу F. Направляти вектор Мо будемо в той бік, звідки поворот, що чиниться силою, видно, що відбувається проти ходу годинникової стрілки. Таким чином, вектор Мо одночасно характеризувати модуль моменту, площину повороту ОАВ, різну для різних сил, і напрямок повороту в цій площині. Точка програми вектора Мо визначає положення центру моменту.

1. Вираз моменту сили за допомогою векторного твору. Розглянемо векторний добуток ОА x F векторів ОА та F (рис. 29). За визначенням,

,

оскільки модуль вектора Мо теж дорівнює 2 пл. ∆ ОАВ. Направлений вектор (ОА x F) перпендикулярно до площини ОАВ, у той бік, звідки найкоротше поєднання ОА з F (якщо їх відкласти від однієї точки) видно проти ходу годинної стрілки, тобто, так, як вектор Мо. Отже, вектори (ОА x F) і Мо збігаються і за модулем і за напрямом і, як легко перевірити, за розмірністю, тобто обидва ці вектори зображають одну й ту саму величину. Звідси

де вектор r = ОА називається радіусом-вектором точки А щодо центру.

Таким чином, момент сили F щодо центру О дорівнює векторному добутку радіуса вектора r =ОА, що з'єднує центр Про з точкою докладання сили А, на саму силу. Цим виразом моменту сили зручно користуватися при доказі деяких теорем.

Час пари сил як вектор.

Дія пари сил на тіло характеризується: 1) величиною модуля моменту пари; 2) площиною дії; 3) напрямком повороту в цій площині. При розгляді пар, що не лежать в одній площині, для характеристики кожної пар необхідно буде задати всі ці три елементи. Це можна зробити, якщо умовитися, за аналогією з моментом сили, зображати момент пари відповідним чином, побудованим вектором, а саме: зображуватимемо момент пари вектором т або М, модуль якого дорівнює (у вибраному масштабі) модулю моменту пари,т. е. добутку однієї з її сил на плече, і який спрямований перпендикулярно до площини дії пари в той бік, звідки поворот пари видно тим, що відбувається проти ходу годинної стрілки (рис. 30).

Як відомо, модуль моменту пари дорівнює моменту однієї з її сил щодо точки, де прикладена інша сила, тобто m = mB(F); за напрямом вектори цих моментів збігаються. Отже

.

Момент сили щодо осі.

Щоб перейти до розв'язання задач статики для випадку довільної просторової системи сил, необхідно запровадити поняття про момент сили щодо осі.

Момент сили щодо осі характеризує обертальний ефект, створюваний силою, що прагне повернути тіло навколо цієї осі. Розглянемо тверде тіло, яке може обертатись навколо деякої осі z (рис. 31). Нехай на це тіло діє сила F, прикладена в точці А. Проведемо через точку А площину ху, перпендикулярну до осі z, і розкладемо силу F на складові: Fz, паралельну осі z, і Fxy , що лежить у площині ху (Fxy є одночасно проекцією сили F на площині ху). Сила Fz, спрямована паралельно осі z, вочевидь, неспроможна повернути тіло навколо цієї осі (вона прагне зрушити тіло вздовж осі z). Весь обертальний ефект, створюваний силою F, співпадатиме з обертальним ефектом її складової Fxy. Звідси укладаємо, що

де символ mxy(F) позначає момент сили F щодо осі z.

Для сили Fxy, що лежить у площині, перпендикулярній до осі z, обертальний ефект вимірюється добутком модуля цієї сили на її відстань h від осі. Але цією ж величиною вимірюється момент сили Fxy щодо точки, у якій вісь z перетинається з площиною xу. Отже або, відповідно до попередньої рівності,

.

В результаті приходимо до наступного визначення: моментом сили щодо осі називається скалярна величина, що дорівнює моменту проекції цієї сили на площину, перпендикулярну до осі, взятому щодо точки перетину осі з площиною.

З креслення (рис. 32) видно, що з обчисленні моменту площину ху можна проводити через будь-яку точку осі z. Таким чином, щоб знайти момент сили щодо осі z (рис. 32) треба:

1. провести площину ху, перпендикулярну до осі z (у будь-якому місці);
2. спроектувати силу F на цю площину та обчислити величину Fxy;
3. опустити з точки Про перетин осі з площиною перпендикуляр на напрямок Fxy і знайти його довжину h;
4. обчислити твір Fxyh;
5. визначити знак моменту.

При обчисленні моментів слід пам'ятати такі окремі випадки:

1. Якщо сила паралельна осі, то її момент щодо осі дорівнює нулю (оскільки Fxy = 0).
2. Якщо лінія дії сили перетинає вісь, то її момент щодо осі також дорівнює нулю (оскільки h = 0).

Об'єднуючи обидва випадки разом, укладаємо, що момент сили щодо осі дорівнює нулю, якщо сила і вісь лежать в одній площині.

1. Якщо сила перпендикулярна до осі, то її момент щодо осі дорівнює добутку модуля сили на відстань між силою та віссю.

Залежність між моментами сили щодо центру та щодо осі.

Нехай на тіло діє прикладена в точці А сила F (рис. 33). Проведемо якусь вісь z і візьмемо на ній довільну точку О. Момент сили F щодо центру Про буде зображатись вектором М0 перпендикулярним до площини ОАВ, причому за модулем

Проведемо тепер через будь-яку точку O1 на осі z площину ху, перпендикулярну до осі; проектуючи силу F на цю площину, знайдемо

Але трикутник О1А1В1 є проекцією трикутника ОАВ на площину xy . Кут між площинами цих трикутників дорівнює куту.між перпендикулярами до площин, тобто дорівнює γ. Тоді, за відомою геометричною формулою, .

Помножуючи обидві частини цієї рівності на 2 і помічаючи, що подвоєні пощади трикутників О1А1В1 і ОАВ рівні відповідно mz(F) і Мо, знайдемо остаточно:

.

Так як твір дає проекцію вектора на вісь z, то рівність можна ще уявити у вигляді

В результаті ми довели, що між моментом сили щодо осі та її моментом щодо якогось центру, що лежить на цій осі, існує наступна залежність: момент сили F щодо осі дорівнює проекції на цю вісь вектора, що зображає момент даної сили щодо будь-якого центру, що лежить на осі.

Приведення просторової системи зусиль до даного центру.

Отримані результати дозволяють вирішити задачу про приведення будь-якої системи сил до даного центру. Це завдання вирішується за допомогою теореми про паралельне перенесення сили. Для перенесення чинної на абсолютно тверде тіло сили F з точки А (рис. 34 а) в точку Про прикладаємо в точці Про сили F' = F і F" = -F. Тоді сила F' = F виявиться прикладеною в точці О і до неї буде приєднана пара (F, F") з моментом т, що можна показати ще так, як на рис. 34, б. При цьому

Розглянемо тепер тверде тіло, на яке діє будь-яка система сил F1, F2, …, Fn (рис. 35, а). Виберемо довільну точку О за центр приведення і перенесемо всі сили системи до цього центру, приєднуючи при цьому відповідні пари. Тоді на тіло діятиме система сил

F '1 = F 1, F '2 = F 2, …, F 'n = Fn.

доданих у центрі О, та система пар, моменти яких дорівнюватимуть

m1 = m0(F1), m2 = m0(F2), …, mn = m0(Fn),

Сили, прикладені в точці, замінюються однією силою R, прикладеної в тій же точці. У цьому чи, .

Щоб скласти усі отримані пари, треба геометрично скласти вектори моментів цих пар. В результаті система пар заміниться однією парою, момент якої або,

Як і у разі плоскої системи, величина R, що дорівнює геометричній сумі всіх сил, називається головним вектором системи; величина Мо, рівна геометричній сумі моментів всіх сил щодо центру, називається головним моментом системи щодо цього центру.

Таким чином ми довели наступну теорему, будь-яка система сил, що діють на абсолютно тверде тіло, при приведенні до довільно взятого центру Про замінюється однією силою R, що дорівнює головному вектору системи і прикладеної в центрі приведення Про, і однією парою з моментом Мо, рівним головному моменту системи щодо центру О (рис. 35, б).

Вектори R і Mо зазвичай визначають аналітично, тобто за їх проекціями на осі координат.

Вирази Rx, Ry, Rz нам відомі.

Проекції вектора Мо на осі координат позначатимемо Mx, My, Mz. За теоремою про проекції суми векторів на вісь буде або,

Mx=My=Mz=0 або коли чинні сили задовольняють умовам

Таким чином, для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей і суми моментів щодо цих осей дорівнювали нулю.

Завдання на рівновагу тіла під впливом просторової системи сил.

Принцип вирішення завдань цього розділу залишається тим самим, що й для плоскої системи сил. Встановивши, рівновага якого тіла буде розглядатися, замінюють накладені на тіло зв'язку їх реакціями і становлять умови рівноваги цього тіла, розглядаючи його як вільне. З отриманих рівнянь визначаються потрібні величини.

Для отримання більш простих систем рівнянь рекомендується осі проводити так, щоб вони перетинали більше невідомих сил або були до них перпендикулярні (якщо це зайве не ускладнює обчислення проекцій та моментів інших сил).

Новим елементом у складанні рівнянь є обчислення моментів сил щодо осей координат.

У випадках, коли із загального креслення важко побачити, чому дорівнює момент даної сили щодо якоїсь осі, рекомендується зобразити на допоміжному кресленні проекцію тіла (разом із силою) на площину, перпендикулярну до цієї осі.

У тих випадках, коли при обчисленні моменту виникають труднощі у визначенні проекції сили на відповідну площину або плеча цієї проекції, рекомендується розкласти силу на дві взаємно перпендикулярні складові (з яких одна паралельна до будь-якої координатної осі), а потім скористатися теоремою Варіньйона.

Вивчення рівноваги тіл з урахуванням тертя зводиться зазвичай до розгляду граничного положення рівноваги, коли сила тертя досягає найбільшого значення . При аналітичному розв'язанні задач реакцію шорсткого зв'язку в цьому випадку зображають двома складовими Nі де. Потім складають звичайні умови рівноваги статики, підставляють у них замість величини, вирішуючи отримані рівняння, визначають шукані величини.

приклад 1.

Розглянемо тіло, що має вертикальну площину симетрії (рис.28). Перетин тіла цієї площини має форму прямокутника. Ширина тіла дорівнює 2 a.

До тіла у точці З, що лежить на осі симетрії, прикладена вертикальна сила і в точці А, що лежить на відстані від основи, горизонтальна сила. Реакція площини основи (реакція зв'язку) приводиться до нормальної реакції та сили тертя. Лінія дії сили невідома. Відстань від точки Здо лінії дії сили позначимо x ().

Рис.28

Складемо три рівняння рівноваги:

Відповідно до закону Кулона, тобто.

Оскільки , то(2)

Проаналізуємо отримані результати:

Збільшуватимемо силу.

Якщо , то рівновага буде мати місце доти, поки сила тертя не досягне своєї граничної величини, умова (1) перетвориться на рівність. Подальше збільшення сили призведе до ковзання тіла поверхнею.

Якщо , то рівновага буде мати місце доти, поки сила тертя не досягне величини, умова (2) перетвориться на рівність. Величина xбуде рівна h. Подальше збільшення сили призведе до того, що тіло перекидатиметься навколо точки B(ковзання не буде).

приклад 2.

На яку максимальну відстань аможе піднятися людина сходами, приставленими до стіни (рис.29)? Якщо вага людини – Р, коефіцієнт тертя ковзання між сходами та стіною – , між сходами та підлогою –.

Рис.29

Розглядаємо рівновагу сходів із людиною. Показуємо силу, нормальні реакції і додаємо сили тертя: і. Вважаємо, що людина знаходиться на відстані, при більшому значенні якої почнеться рух сходів. Складаємо рівняння рівноваги.

Підставивши значення сил тертя та розв'язавши систему рівнянь, отримаємо

Тепер можна визначити кут під яким треба поставити сходи, щоб дістатися до стіни. Вважаючи , отримаємо, після перетворень, і

Рис.30

Зауважимо, що й рівнодіюча всіх активних сил (всіх крім реакцій) спрямовано під кутом(рис.30), то нормальна реакція, а сила тертя. Для того, щоб почалося ковзання, має виконуватися умова. або. І оскільки , то . Значить кут має бути більшим за кут. Отже, якщо сила діє всередині кута або конуса тертя (), то як би була велика ця сила, ковзання тіла не відбудеться. Така умова називається умовою заклинювання, самогальмування.

Ми розглянули ковзання твердих тіл на поверхні. Але нерідко зустрічається ковзання гнучких тіл по неплоскій поверхні. Наприклад, небажане прослизання в ременной передачі ременя по шківу, або троса, каната, намотаного на нерухомий циліндр.

Приклад 3.

Нехай є нитка, перекинута через нерухому циліндричну поверхню (рис.31). За рахунок сил тертя натяг лівого та правого кінців цієї нитки будуть різними.

Рис.31 Рис.32

Припустимо, нормальна реакція і сила тертя розподіляються рівномірно по дузі контакту нитки на циліндрі. Розглянемо рівновагу ділянки нитки завдовжки. (Рис.32). На лівому кінці цієї ділянки натяг, правому. Складаємо рівняння рівноваги, проектуючи сили на осі:

Так як кут - мала величина, то вважаємо З урахуванням цього з рівнянь знаходимо, тому що, маємо або інтегруючи, отримаємо . Або

Цей результат називається формулою Ейлер.

Наприклад, якщо нитка перекинута через нерухомий шків і коефіцієнт тертя, то відношення натягу . А, обернувши циліндр один раз (), тобто можна утримати вантаж на іншому кінці нитки силою майже втричі меншою за вагу тіла.

Якщо тіло, що розглядається, має форму катка і під дією прикладених активних сил може котитися по поверхні іншого тіла, то через деформацію поверхонь цих тіл у місці дотику можуть виникнути сили реакції, що перешкоджають не тільки ковзанню, але і коченню. Прикладами таких котків є різні колеса, як, наприклад, у електровозів, вагонів, автомашин, кульки та ролики в кулькових та роликових підшипниках тощо.

Нехай циліндрична ковзанка знаходиться на горизонтальній площині під дією активних сил. Дотик котка з площиною через деформацію фактично відбувається не вздовж однієї утворюючої, як у випадку абсолютно твердих тіл, а по деякому майданчику. Якщо активні сили прикладені симетрично щодо середнього перерізу котки, тобто викликають однакові деформації вздовж усієї його утворюючої, то можна вивчати лише один середній переріз котки. Цей випадок розглянуто нижче.

Між котком і площиною, на якій він спочиває, виникають сили тертя, якщо прикласти до осі катка силу (мал. 7.5), що прагне рухати його по площині.

Розглянемо випадок, коли сила паралельна горизонтальній площині. З досвіду відомо, що з зміні модуля сили від нуля до деякого граничного значення ковзанка залишається у спокої, тобто. сили, що діють на ковзанку, врівноважуються. Крім активних сил (ваги та сили ), до котка, рівновага якого розглядається, прикладена реакція площини. З умови рівноваги трьох непаралельних сил випливає, що реакція площини має проходити через центр катка Про, тому що дві інші сили прикладені до цієї точки.

Отже, точка застосування реакції Зповинна бути зміщена на деяку відстань від вертикалі, що проходить через центр колеса, інакше реакція не матиме горизонтальної складової, необхідної для задоволення умов рівноваги. Розкладемо реакцію площини на дві складові: нормальну складову та дотичну реакцію, що є силою тертя (рис. 7.6).

У граничному положенні рівноваги ковзанки до нього будуть прикладені дві пари, що взаємно врівноважуються: одна пара сил (, ) з моментом (де r– радіус катка) та друга пара сил ( , ), що утримує каток у рівновазі.

Момент пари, званої моментом тертя кочення, Визначається формулою:

,

з якої випливає, що для того, щоб мало місце чисте кочення (без ковзання), необхідно, щоб сила тертя кочення була меншою за максимальну силу тертя ковзання:

де f- Коефіцієнт тертя ковзання.

Таким чином, чисте кочення (без ковзання) буде, якщо .

Тертя кочення виникає через деформацію ковзанки і площини, внаслідок чого зіткнення між ковзанкою і площиною відбувається по деякій поверхні, зміщеній від нижньої точки катка у бік можливого руху.

Якщо сила не спрямована по горизонталі, її слід розкласти на дві складові, спрямовані по горизонталі і вертикалі. Вертикальну складову слід скласти із силою, і ми знову приходимо до схеми дії сил, зображених на рис. 7.6.

Встановлено такі наближені закони для максимального моменту пари сил, що перешкоджає коченню:

1. Найбільший момент пари сил, що перешкоджає коченню, у досить широких межах не залежить від радіусу котка.

2. Граничне значення моменту пропорційно до нормального тиску та рівної йому нормальної реакції: .

Коефіцієнт пропорційності d називають коефіцієнтом тертя кочення при спокоїабо коефіцієнтом тертя другого роду. Коефіцієнт d має розмірність довжини.

3. Коефіцієнт тертя кочення d залежить від матеріалу катка, площини та фізичного стану їх поверхонь. Коефіцієнт тертя при коченні в першому наближенні можна вважати таким, що не залежить від кутової швидкості кочення котка і його швидкості ковзання по площині. Для випадку кочення вагонного колеса по сталевій рейці коефіцієнт тертя кочення.

Закони тертя кочення, як і закони тертя ковзання, справедливі для невеликих нормальних тисків і не дуже легко деформуються матеріалів катка і площини.

Ці закони дозволяють не розглядати деформації ковзанки та площини, вважаючи їх абсолютно твердими тілами, що стосуються однієї точки. У цій точці дотику крім нормальної реакції та сили тертя треба прикласти ще й пару сил, що перешкоджають коченню.

Для того, щоб ковзанка не ковзала, необхідно виконання умови

.

Для того щоб ковзанка не котилася, повинна виконуватися умова

Рішення: Складемо рівняння рівноваги в проекціях на осі координат:

; ;

Т.к. , Виразимо з другого рівняння нормальну реакцію поверхні: тоді . Підставимо отриманий вираз у перше рівняння:

Підставивши відомі чисельні значення, отримаємо:

Тобто. величина проекції сили тяжіння перевищує величину проекції граничної сили тертя, отже, тіло перебуває у рівновазі і ковзає.

Для знаходження величини сили тертя (рис. 7.8) підставимо чисельні значення раніше отриманий вираз для цієї сили:

кн.

Відповідь: тіло ковзає; кн.

Самостійно вирішіть наступні тестові завдання:

Тіло вагою G= 10 (Н) утримується в рівновазі на шорсткій похилій площині (рис. 7.13) з кутом нахилу α=30° (коефіцієнт тертя ковзання f=0,2) силою (Н).

Мінімальне значення сили S, що утримує тіло від переміщення внизпо похилій площині, рівно …

Рис. 7.13

Варіанти відповідей: 1) 6,7 2) 3,3 3) 7,6 4) 9,6

Тіло вагою G= 10 (Н) утримується в рівновазі на шорсткій похилій площині (рис. 7.14) з кутом нахилу α=45° (коефіцієнт тертя ковзання f=0,2) силою (Н).

3.4.1 Рівновість твердого тіла за наявності тертя ковзання

Тертям ковзанняназивається опір, що виникає при відносному ковзанні двох дотичних тіл.

Величина сили тертя ковзання пропорційна нормальному тиску одного з дотичних тіл на інше:

Реакція шорсткої поверхні відхилена від нормалі деякий кут φ (рис. 3.7). Найбільший кут, який повна реакція шорсткого зв'язку утворює з нормаллю до поверхні, називається кутом тертя.

де статичний коефіцієнт тертя.

Цей коефіцієнт зазвичай більше коефіцієнта тертя під час руху.

З рис. 3.7 видно, що кут тертя дорівнює значенню

. (3.26)

Рівність (3.26) виражає зв'язок між кутом тертя та коефіцієнтом тертя.

Методика вирішення завдань статики за наявності тертя залишається такою ж, як і у разі відсутності тертя, тобто зводиться до складання та вирішення рівнянь рівноваги. При цьому реакцію шорсткої поверхні слід уявити двома складовими - нормальною реакцією та силою тертя.

Слід пам'ятати, що у таких завданнях розрахунок ведеться зазвичай на максимальну величину сили тертя, що визначається формулою (3.25).

Приклад 3.6:

Вантаж А ваги Qлежить на шорсткої площині, нахиленої до

горизонту під кутом α, і утримується ниткою, намотаною на щабель блоку радіусу R.При якій вазі Рвантажу В система перебуватиме в рівновазі, якщо коефіцієнт тертя ковзання вантажу об площину дорівнює f, а радіус меншого ступеня блоку (рис. 3.8).

Розглянемо рівновагу вантажу У, який діє сила тяжкості і реакція нитки , причому чисельно (рис. 3.8 , а). На вантаж А діють сила тяжкості, реакція нитки, нормальна реакція похилої площини та сила тертя. Оскільки радіус rменшого ступеня блоку в два рази менше більшого ступеня, то в положенні рівноваги , або

Розглянемо випадок, за якого існує рівновага вантажу А, але так, що збільшення сили тяжіння Pвантажу Викличе переміщення вантажу А вгору (рис. 3.8, б). У цьому випадку сила тертя спрямована вниз похилою площиною, причому . Виберемо осі х і у, зазначені на малюнку, і складемо два рівняння рівноваги системи сил, що сходяться на площині:

(3.27)

Отримаємо, що , тоді сила тертя .

Підставимо на рівність (3.27) значення і , знайдемо величину Р:

Тепер розглянемо випадок коли існує рівновага вантажу А, але так, що зменшення сили тяжіння Рвантажу Викличе переміщення вантажу А вниз (рис. 3.8, в). Тоді сила тертя буде спрямована вгору похилою площиною. Оскільки значення Nне зміниться, достатньо скласти одне рівняння в проекції на вісь х:

. (3.29)

Підставивши в рівність (3.29) значення і отримаємо, що

Таким чином, рівновага даної системи буде можлива за умови

3.4.2. Рівновість твердого тіла за наявності тертя кочення

Тертям коченняназивається опір, що виникає при коченні одного тіла поверхнею іншого.

Уявлення про природу тертя кочення можна отримати, виходячи межі статики твердого тіла. Розглянемо циліндричний каток радіусу Rта ваги Р, що спирається на горизонтальну площину. Прикладемо до осі катка силу , меншу за силу тертя (рис. 3.9, а). Тоді сила тертя, чисельно рівна, перешкоджає ковзанню циліндра по площині. Якщо нормальна реакція прикладена в точці А, вона врівноважує силу , а сили і утворюють пару, що викликає кочення циліндра навіть при малому значенні сили S.

Насправді, внаслідок деформацій тіл дотик їх відбувається вздовж деякої площі АВ (рис. 3.9 б). При дії сили інтенсивність тиску точки А зменшується, а у точки В зростає. В результаті нормальна реакція зміщується у бік дії сили на величину k, Яка називається коефіцієнтом тертя кочення Цей коефіцієнт вимірюється у одиницях довжини.

В ідеальному положенні рівноваги катка до нього будуть прикладені дві пари, що взаємно врівноважуються: одна пара сил з моментом і друга пара сил , що утримує каток в рівновазі. Момент пари, званий моментом тертя кочення, визначається формулою

З цієї рівності випливає, що для того, щоб мало місце чисте кочення (без ковзання), необхідно, щоб сила тертя кочення була меншою за максимальну силу тертя ковзання: , де f- Коефіцієнт тертя ковзання. Таким чином, чисте кочення можливе за умови .

Слід розрізняти напрямок зміщення точки докладання нормальної реакції ведучого та веденого колеса. Для ведучого колеса деформаційний валик, що викликає зміщення точки докладання нормальної реакції площини, знаходиться ліворуч від його центру, якщо колесо буде рухатися вправо. Тому для цього колеса напрямок сили тертя збігається з напрямком його руху (рис. 3.10, а). У веденому колесі деформаційний валик зміщений щодо центру в напрямку руху. Отже, сила тертя у разі спрямована убік, протилежну напрямку руху центру колеса.

Приклад 3.7:

Циліндр ваги Р=10 Н та радіуса R= 0,1 м знаходиться на шорсткої площині, нахиленої під кутом α = 30˚ до горизонту. До осі циліндра прив'язана нитка, перекинута через блок і несуча на іншому кінці вантаж В. При якій вазі Qвантажу В циліндр не покотиться, якщо коефіцієнт тертя кочення дорівнює k= 0,01 м (рис. 3.11 а)?

Розглянемо рівновагу циліндра у двох випадках. Якщо величина сили Qмає найменше значення, то можливий рух циліндра вниз по похилій площині (рис. 3.11 б). До циліндра прикладено вагу циліндра та натяг нитки. В цьому випадку нормальна реакція похилої площини буде зміщена на відстань kліворуч від перпендикуляра, опущеного із центру циліндра на похилу площину. Сила тертя спрямована вздовж похилої площини протилежно до можливого руху центру циліндра.

Рис. 3.11

Для визначення значення достатньо скласти рівняння рівноваги щодо точки З. При обчисленні моменту сили щодо цієї точки силу розкладемо на складові: складова перпендикулярна до похилої площини, а складова паралельна цій площині. Момент сили і щодо точки С дорівнюють нулю, тому що вони прикладені в цій точці:

Звідки

У другому випадку, коли сила Qдосягає максимального значення, можливе переміщення центру циліндра вгору похилою площиною (рис. 3.11, в). Тоді сили і будуть спрямовані аналогічно до першого випадку. Реакція похилої площини буде прикладена в точці і зміщена на відстань kправоруч по похилій площині. Сила тертя спрямована протилежно до можливого руху центру циліндра. Складемо рівняння моментів щодо точки.

Якщо два тіла I і II (рис. 6.1) взаємодіють одне з одним, стикаючись у точці А, то завжди реакцію RA , що діє, наприклад, з боку тіла II і прикладена до тіла I, можна розкласти на дві складові: NA , спрямовану по загальної нормалі до поверхні дотичних тіл у точці А і Т А, що лежить в дотичній площині. Складова N A називається нормальною реакцією, сила Т А називається силою тертя ковзання - вона перешкоджає ковзанню тіла I по тілу II. Відповідно до аксіоми 4 (третій закон Ньютона) на тіло II з боку тіла I діє рівна за модулем і протилежно спрямована сила реакції. Її складова, перпендикулярна дотичній площині, називається силою нормального тиску. Сила тертя Т А = 0, якщо дотичні поверхні ідеально гладкі. У реальних умовах поверхні шорсткі і в багатьох випадках знехтувати силою тертя не можна. Максимальна сила тертя приблизно пропорційна нормальному тиску, тобто T max =fN. (6.3) - закон Амонтона-Кулона. Коефіцієнт f називається коефіцієнтом тертя ковзання. Його значення не залежить від площі дотичних поверхонь, але залежить від матеріалу і ступеня шорсткості дотичних поверхонь. Силу тертя можна вирахувати по ф-ле T=fN тільки якщо має місце критичний випадок. В інших випадках силу тертя слід визначати з рівнів ур. На малюнку показано реакцію R (тут активні сили прагнуть зрушити тіло вправо). Кут j між граничною реакцією R та нормаллю до поверхні називається кутом тертя. tgj = Tmax / N = f.

Геометричне місце всіх можливих напрямів граничної реакції R утворює конічну поверхню - конус тертя (рис. 6.6 б). Якщо коефіцієнт тертя f у всіх напрямках однаковий, то конус тертя буде круговим. У тих випадках, коли коефіцієнт тертя f залежить від напрямку можливого руху тіла, конус тертя не буде круговим. Якщо рівнодіюча активна сила. знаходиться всередині конуса тертя, збільшенням її модуля не можна порушити рівновагу тіла; Для того щоб тіло почало рух, необхідно (і достатньо), щоб рівнодіюча активних сил F знаходилася поза конусом тертя. Розглянемо тертя гнучких тіл (рис.6.8). Формула Ейлера допомагає знайти найменшу силу P, здатну врівноважити силу Q. P = Qe -fj *. Можна також знайти таку силу P, здатну подолати опір тертя разом із силою Q. У цьому випадку у формулі Ейлера зміниться тільки знак f: P = Qe f j *.