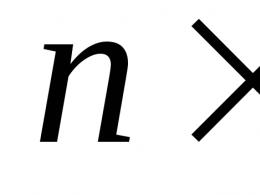Визначення пре. Межа функції: основні поняття та визначення. b. Межа функції з бази

Наводяться визначення межі функції по Гейне (через послідовності) і Коші (через эпсилон і дельта околиці). Визначення даються в універсальному вигляді, що застосовується як для двосторонніх, так і односторонніх меж у кінцевих та нескінченно віддалених точках. Розглянуто визначення, що точка a не є межею функції. Доказ еквівалентності визначень по Гейні та Коші.

Див. також: Околиця точки
Визначення межі функції у кінцевій точці
Визначення межі функції на нескінченності

Перше визначення межі функції (за Гейном)

(x)у точці x 0 :
,
якщо
1) існує така проколота околиця точки x 0
2) для будь-якої послідовності ( x n ), що сходить до x 0 :
, елементи якої належать околиці ,
послідовність ( f(x n ))сходиться до a:
.

Тут x 0 і можуть бути як кінцевими числами, так і нескінченно віддаленими точками. Околиця може бути як двосторонньою, так і односторонньою.

.

Друге визначення межі функції (за Кошою)

Число a називається межею функції f (x)у точці x 0 :
,
якщо
1) існує така проколота околиця точки x 0 , де функція визначена;
2) для будь-якого позитивного числа ε > 0 існує таке число δε > 0 , що залежить від ε , що для всіх x , що належать проколоті δ ε - околиці точки x 0 :
,
значення функції f (x)належать ε - околиці точки a:
.

Крапки x 0 і можуть бути як кінцевими числами, так і нескінченно віддаленими точками. Околиця також може бути як двосторонньою, так і односторонньою.

Запишемо це визначення за допомогою логічних символів існування та загальності:
.

У цьому вся визначенні використовуються околиці з рівновіддаленими кінцями. Можна дати і еквівалентне визначення, використовуючи довільні околиці точок.

Визначення з використанням довільних околиць
Число a називається межею функції f (x)у точці x 0 :
,
якщо
1) існує така проколота околиця точки x 0 , де функція визначена;
2) для будь-якого околиці U (a)точки a існує така проколота околиця точки x 0 , що для всіх x , що належать проколоті околиці точки x 0 :
,
значення функції f (x)належать околиці U (a)точки a:
.

За допомогою логічних символів існування та загальності це визначення можна записати так:
.

Односторонні та двосторонні межі

Наведені вище визначення універсальні тому, що їх можна використовувати будь-яких типів околиць. Якщо, як ми використовуємо ліву проколоту околицю кінцевої точки, то отримаємо визначення лівосторонньої межі . Якщо як околиця використовувати околицю нескінченно віддаленої точки, то отримаємо визначення межі на нескінченності.

Для визначення межі за Гейном це зводиться до того, що на довільну, що сходить до послідовність накладається додаткове обмеження - її елементи повинні належати відповідній проколоті околиці точки.

Для визначення межі по Коші необхідно у кожному разі перетворити висловлювання й у нерівності, використовуючи відповідні визначення околиці точки.
Див. «Навколо точки».

Визначення, що точка a не є межею функції

Часто виникає необхідність використовувати умову, що точка a не є межею функції при . Побудуємо заперечення до викладених вище ухвал. Вони ми припускаємо, що функція f (x)визначена на деякому проколоті околиці точки x 0 . Точки a та x 0 можуть бути як кінцевими числами, так і нескінченно віддаленими. Все сформульоване нижче стосується як двосторонніх, так і односторонніх меж.

По Гейні.
Число a не ємежею функції f (x)у точці x 0 : ,
якщо існує така послідовність ( x n ), що сходить до x 0 :
,
елементи якої належать околиці,
що послідовність ( f(x n ))не сходиться до a:
.
.

По Коші.
Число a не ємежею функції f (x)у точці x 0 :
,
якщо існує така позитивна кількість ε > 0 так для будь-якого позитивного числа δ > 0 існує таке x , що належить проколотій δ - околиці точки x 0 :
,
що значення функції f (x)не належить ε - околиці точки a:
.
.

Зрозуміло, якщо точка a не є межею функції при , то це не означає, що в неї не може бути межі. Можливо, існує межа , але вона не дорівнює a . Також можливий випадок, коли функція визначена в проколоті околиці точки , але не має межі при .

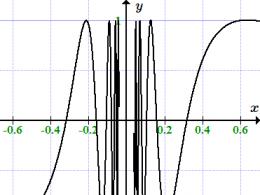
Функція f(x) = sin(1/x)не має межі за x → 0.

Наприклад, функція визначена при , але межі немає. Для доказу візьмемо послідовність. Вона сходиться до точки 0 : . Оскільки, то.
Візьмемо послідовність. Вона також сходиться до точки 0 : . Але оскільки, то.
Тоді межа не може дорівнювати жодному числу a. Дійсно, при , Існує послідовність , З якої . Тому будь-яке відмінне від нуля число не є межею. Але також не є межею, оскільки існує послідовність , з якою .

Еквівалентність визначень межі по Гейні та Коші

Теорема
Визначення межі функції по Гейні та Коші еквівалентні.

Доказ

При доказі ми припускаємо, що функція визначена в деякій проколоті околиці точки (кінцевої або нескінченно віддаленої). Точка a також може бути кінцевою чи нескінченно віддаленою.

Доказ Гейне ⇒ Коші

Нехай функція має у точці межу a згідно з першим визначенням (за Гейном). Тобто для будь-якої послідовності, що належить проколоті околиці точки і має межу
(1) ,
межа послідовності дорівнює a:
(2) .

Покажемо, що функція має межу в точці Коші. Тобто для кожного існує, що для всіх.

Допустимо неприємне. Нехай умови (1) та (2) виконані, але функція не має межі по Коші. Тобто існує таке, що для будь-кого існує, так що
.

Візьмемо , де n – натуральне число. Тоді існує , причому
.
Таким чином ми побудували послідовність, що сходить до, але межа послідовності не дорівнює a. Це суперечить умові теореми.

Перша частина – доведена.

Доказ Коші ⇒ Гейне

Нехай функція має у точці межу a згідно з другим визначенням (за Кошою). Тобто для будь-кого існує, що
(3) для всіх .

Покажемо, що функція має межу a у точці за Гейном.
Візьмемо довільне число. Згідно з визначенням Коші існує число , так що виконується (3).

Візьмемо довільну послідовність, що належить проколотому околиці і сходить до. За визначенням послідовності, що сходить, для будь-якого існує , що
при .
Тоді з (3) випливає, що
при .
Оскільки це виконується для будь-кого, то
.

Теорему доведено.

Використана література:
Л.Д. Кудрявці. Курс математичного аналізу. Том 1. Москва, 2003.

У цій статті ми розповімо, що являє собою межу функції. Спочатку пояснимо загальні моменти, які дуже важливі для розуміння суті цього явища.

Поняття межі

У математиці принципово важливим є поняття нескінченності, яке позначається символом ∞. Його слід розуміти як нескінченно велике + ∞ або нескінченно мале - ∞ число. Коли ми говоримо про нескінченність, часто ми маємо на увазі відразу обидва ці її сенси, проте запис виду + ​​∞ або - ∞ не варто замінювати просто на ∞.

Запис межі функції має вигляд lim x x 0 f (x) . У нижній частині ми пишемо основний аргумент x , а за допомогою стрілочки вказуємо, якого саме значення x 0 він буде прагнути. Якщо значення x 0 є конкретним дійсним числом, ми маємо справу з межею функції в точці. Якщо ж значення x 0 прагне нескінченності (не важливо, ∞ , + ∞ або - ∞), то слід говорити про межу функції на нескінченності.

Межа буває кінцевою і нескінченною. Якщо він дорівнює конкретному дійсному числу, тобто. lim x → x 0 f (x) = A , то його називають кінцевою межею, якщо ж lim x → x 0 f (x) = ∞ , lim x → x 0 f (x) = + ∞ або lim x → x 0 f (x) = - ∞ , то нескінченним.

Якщо ми не можемо визначити ні кінцеве, ні нескінченне значення, це означає, що такої межі немає. Прикладом цього випадку може бути межа від синусу на нескінченності.

У цьому пункті ми пояснимо, як знайти значення межі функції у точці та на нескінченності. Для цього нам потрібно запровадити основні визначення та згадати, що таке числові послідовності, а також їх збіжність та розбіжність.

Визначення 1

Число A є межею функції f (x) при x → ∞ , якщо послідовність її значень буде схожа на A для будь-якої нескінченно великої послідовності аргументів (негативної або позитивної).

Запис межі функції має такий вигляд: lim x → ∞ f (x) = A .

Визначення 2

При x → ∞ межа функції f (x) є нескінченною, якщо послідовність значень для будь-якої нескінченно великої послідовності аргументів буде також нескінченно великою (позитивною або негативною).

Запис виглядає як lim x → f (x) = ∞ .

Приклад 1

Доведіть рівність lim x → ∞ 1 x 2 = 0 за допомогою основного визначення межі x → ∞ .

Рішення

Почнемо із запису послідовності значень функції 1 x 2 для нескінченно великої позитивної послідовності значень аргументу x = 1, 2, 3,. . . , n, . . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 n 2 > . . .

Ми бачимо, що значення поступово зменшуватимуться, прагнучи до 0 . на картинці:

x = - 1, - 2, - 3,. . . , - n , . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . >1-n2>. . .

Тут теж видно монотонне спадання нанівець, що підтверджує вірність даного за умови рівності:

Відповідь:Вірність цього за умови рівності доведено.

Приклад 2

Обчисліть межу lim x → ∞ e 1 10 x .

Рішення

Почнемо, як і раніше, із запису послідовностей значень f(x) = e 1 10 x для нескінченно великої позитивної послідовності аргументів. Наприклад, x = 1, 4, 9, 16, 25,. . . , 10 2 , . . . → + ∞.

e 1 10; e 4 10; e 9 10; e 16 10; e 25 10; . . . ; e 100 10; . . . = = 1, 10; 1, 49; 2, 45; 4, 95; 12, 18; . . . ; 22026, 46; . . .

Ми бачимо, що дана послідовність нескінченно позитивна, отже, f(x) = lim x → + ∞ e 1 10 x = + ∞

Переходимо до запису значень нескінченно великої негативної послідовності, наприклад, x = - 1, - 4, - 9, - 16, - 25,. . . , - 10 2 ,. . . → - ∞.

e-110; e-4 10 ; e-9 10 ; e-16 10 ; e-25 ​​10 ; . . . ; e-100 10 ; . . . = = 0,90; 0, 67; 0, 40; 0, 20; 0, 08; . . . ; 0, 000045; . . . x = 1, 4, 9, 16, 25,. . . , 10 2 , . . . → ∞

Оскільки вона теж прагне нуля, то f (x) = lim x → ∞ 1 e 10 x = 0 .

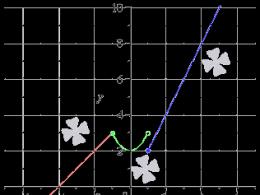
Наочно розв'язання задачі показано на ілюстрації. Синіми точками відзначено послідовність позитивних значень, зеленими – негативних.

Відповідь: lim x → ∞ e 1 10 x = + ∞ , п р і x → + ∞ 0 , п р і x → - ∞ .

Перейдемо методу обчислення межі функції у точці. Для цього нам потрібно знати, як правильно визначити односторонню межу. Це стане нам у нагоді і для того, щоб знайти вертикальні асимптоти графіка функції.

Визначення 3

Число B є межею функції f (x) зліва при x → a у тому випадку, коли послідовність її значень сходить до даного числа при будь-якій послідовності аргументів функції x n , що сходить до a якщо при цьому її значення залишаються менше a (x n< a).

Така межа на листі позначається як lim x → a – 0 f (x) = B .

Тепер сформулюємо, що таке межа функції праворуч.

Визначення 4

Число B є межею функції f (x) праворуч при x → a у тому випадку, коли послідовність її значень сходить до даного числа при будь-якій послідовності аргументів функції xn , що сходить до a якщо при цьому її значення залишаються більше a (xn > a) .

Цю межу записуємо як lim x → a + 0 f (x) = B .

Ми можемо визначити межу функції f (x) у певній точці тоді, коли неї існують рівні межі з лівої і правої боку, тобто. lim x → f (x) = lim x → a - 0 f (x) = lim x → a + 0 f (x) = B . У разі нескінченності обох меж межа функції у вихідній точці також буде нескінченною.

Тепер ми роз'яснимо дані визначення, записавши рішення конкретного завдання.

Приклад 3

Доведіть, що існує кінцева межа функції f(x) = 1 6 (x - 8) 2 - 8 у точці x 0 = 2 та обчисліть його значення.

Рішення

Для того, щоб вирішити задачу, нам потрібно згадати визначення межі функції у точці. Спочатку доведемо, що з вихідної функції є межа зліва. Запишемо послідовність значень фукнції, яка буде сходитися до x 0 = 2 якщо x n< 2:

f (- 2); f(0); f(1); f 1 1 2; f 1 3 4; f 1 7 8; f 1 15 16; . . . ; f 1 1023 1024; . . . = = 8, 667; 2, 667; 0, 167; - 0,958; - 1, 489; - 1, 747; - 1, 874; . . . ; - 1, 998; . . . → - 2

Оскільки наведена послідовність зводиться до - 2 ми можемо записати, що lim x → 2 - 0 1 6 x - 8 2 - 8 = - 2 .

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Значення функції у цій послідовності виглядатимуть так:

f(6); f(4); f(3); f 2 1 2; f 2 3 4; f 2 7 8; f 2 15 16; . . . ; f 2 1023 1024; . . . = = - 7, 333; - 5, 333; - 3, 833; - 2, 958; - 2, 489; - 2, 247; - 2, 124; . . . , - 2, 001,. . . → - 2

Ця послідовність також сходиться до - 2 , отже, lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2 .

Ми отримали, що межі з правої та лівої сторони у цієї функції будуть рівними, отже, межа функції f(x) = 1 6 (x - 8) 2 - 8 у точці x 0 = 2 існує, і lim x → 2 1 6 (x – 8) 2 – 8 = – 2 .

Ви можете побачити хід рішення на ілюстрації (зелені точки – послідовність значень, що сходяться до x n< 2 , синие – к x n > 2).

Відповідь:Межі з правої та лівої сторони цієї функції будуть рівними, значить, межа функції існує, і lim x → 2 1 6 (x - 8) 2 - 8 = - 2 .

Щоб глибше вивчити теорію меж, радимо вам прочитати статтю про безперервність функції у точці та основні види точок розриву.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Межа функції- Число aбуде межею деякої величини, що змінюється, якщо в процесі своєї зміни ця змінна величина необмежено наближається до a.

Або іншими словами, число Aє межею функції y = f(x)у точці x 0, якщо для будь-якої послідовності точок з області визначення функції , не рівних x 0, і яка сходиться до точки x 0 (lim x n = x0), послідовність відповідних значень функції сходиться до A.

Графік функції, межа якої при аргументі, що прагне нескінченності, дорівнює L:

Значення Ає межею (граничним значенням) функції f(x)у точці x 0у випадку, якщо для будь-якої послідовності точок , яка сходиться до x 0, але яка не містить x 0як один зі своїх елементів (тобто в проколоті околиці x 0), послідовність значень функції сходиться до A.

Межа функції по Коші.

Значення Aбуде межею функції f(x)у точці x 0у випадку, якщо для кожного вперед взятого негативного числа ε буде знайдено відповідне йому невід'ємне число δ = δ(ε) таке, що для кожного аргументу x, що задовольняє умові 0 < | x - x0 | < δ , буде виконано нерівність | f(x) A |< ε .

Буде дуже просто, якщо ви розумієте суть межі та основні правила знаходження його. Те, що межа функції f (x)при xщо прагне до aдорівнює A, записується таким чином:

Причому значення, якого прагне змінна x, може бути не тільки числом, а й нескінченністю (∞), іноді +∞ або -∞, або межі взагалі не може бути.

Щоб зрозуміти, як знаходити межі функції, найкраще подивитись приклади рішення.

Необхідно визначити межі функції f (x) = 1/xпри:

x→ 2, x→ 0, x→ ∞.

Знайдемо рішення першої межі. Для цього можна просто підставити замість xчисло, якого вона прагне, тобто. 2, отримаємо:

Знайдемо другу межу функції. Тут підставляти у чистому вигляді 0 замість xне можна, т.к. ділити на 0 не можна. Але ми можемо брати значення, наближені до нуля, наприклад, 0,01; 0,001; 0,0001; 0,00001 і так далі, причому значення функції f (x)збільшуватиметься: 100; 1000; 10000; 100000 і так далі. В.о., можна зрозуміти, що за x→ 0 значення функції, що стоїть під знаком межі, необмежено зростатиме, тобто. прагнути до нескінченності. А значить:

Стосовно третьої межі. Така ж ситуація, як і в минулому випадку, неможливо підставити ∞ В чистому вигляді. Потрібно розглянути випадок необмеженого зростання x. По черзі підставляємо 1000; 10000; 100000 і так далі маємо значення функції f (x) = 1/xбуде спадати: 0,001; 0,0001; 0,00001; і так далі, прагнучи нуля. Тому:

Необхідно обчислити межу функції

Приступаючи до вирішення другого прикладу, бачимо невизначеність. Звідси знаходимо старший ступінь чисельника та знаменника - це x 3, Виносимо в чисельнику та знаменнику його за дужки і далі скорочуємо на нього:

Відповідь

Першим кроком у знаходженні цієї межі, підставимо значення 1 замість x, у результаті маємо невизначеність . Для її вирішення розкладемо чисельник на множники, зробимо це методом знаходження коріння квадратного рівняння x 2 + 2x - 3:

D = 2 2 - 4 * 1 * (-3) = 4 +12 = 16→ √ D =√16 = 4

x 1,2 = (-2±4)/2→ x 1 = -3;x 2= 1.

Таким чином, чисельник буде таким:

Відповідь

Це визначення його конкретного значення або певної області, куди потрапляє функція обмежена межею.

Щоб вирішити межі, дотримуйтесь правил:

Розібравшись у суті та основних правилах вирішення межі, Ви отримаєте базове поняття про те, як їх вирішувати.

Розглянемо функцію %%f(x)%%, визначену, принаймні, в деякому проколоті околиці %%\stackrel(\circ)(\text(U))(a)%% точки %%a \in \overline( \mathbb(R))%% розширеної числової прямої.

Поняття межі по Коші

Число %%A \in \mathbb(R)%% називають межею функції%%f(x)%% у точці %%a \in \mathbb(R)%% (або при %%x%%, що прагне до %%a \in \mathbb(R)%%), якщо, яке б не було позитивне число %%\varepsilon%%, знайдеться позитивне число %%\delta%%, таке, що для всіх точок проколотою %%\delta%%-околиці точки %%a%% значення функції належать %%\varepsilon %%-околиці точки %%A%%, або

$$ A = \lim\limits_(x \to a)(f(x)) \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Rightarrow f(x) \in \text(U)_\varepsilon (A) \big) $$

Це визначення називається визначенням мовою %%varepsilon%% і %%delta%%, запропоноване французьким математиком Огюстеном Коші і використовується з початку XIX століття по теперішній час, оскільки має необхідну математичну строгість і точність.

Комбінуючи різні околиці точки %%a%% виду %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta^- (a) %% з околицями %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \text(U) _\varepsilon (-\infty)%%, отримаємо 24 визначення межі по Коші.

Геометричний сенс

Геометричний сенс межі функції

З'ясуємо, у чому полягає геометричний сенс межі функції у точці. Побудуємо графік функції %% y = f (x) % % і відзначимо на ньому точки % % x = a % % і % % y = A % %.

Межа функції %%y = f(x)%% у точці %%x \to a%% існує і дорівнює A, якщо для будь-якої %%\varepsilon%%-околиці точки %%A%% можна вказати таку %%\ delta%%-околиця точки %%a%%, що для будь-якого %%x%% з цієї %%\delta%%-околиці значення %%f(x)%% буде знаходитися в %%\varepsilon%%-околиці точки %%A%%.

Зазначимо, що за визначенням межі функції по Коші для існування межі при %%x \to a%% не важливо, яке значення набуває функція в самій точці %%a%%. Можна навести приклади, коли функція не визначена при %%x = a%% або приймає значення, відмінне від %%A%%. Проте межа може дорівнювати %%A%%.

Визначення межі за Гейном

Елемент %%A \in \overline(\mathbb(R))%% називається межею функції %%f(x)%% при %% x \to a, a \in \overline(\mathbb(R))%% , якщо для будь-якої послідовності %%\(x_n\) \to a%% з області визначення, послідовність відповідних значень %%\big\(f(x_n)\big\)%% прагне %%A%%.

Визначення межі по Гейне зручно використовувати, коли виникають сумніви щодо існування межі функції у цій точці. Якщо можна побудувати хоча б одну послідовність %%\(x_n\)%% з межею в точці %%a%% таку, що послідовність %%\big\(f(x_n)\big\)%% не має межі, то можна зробити висновок про те, що функція %%f(x)%% не має межі у цій точці. Якщо для двох різнихпослідовностей %%\(x"_n\)%% та %%\(x""_n\)%%, що мають однаковиймежа %%a%%, послідовності %%\big\(f(x"_n)\big\)%% та %%\big\(f(x""_n)\big\)%% мають різнімежі, то цьому випадку також немає межа функції %%f(x)%%.

Приклад

Нехай %%f(x) = \sin(1/x)%%. Перевіримо, чи існує межа цієї функції у точці %%a = 0%%.

Виберемо спочатку послідовність, що сходить до цієї точки, $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\). $$

Ясно, що %%x_n \ne 0~\forall~n \in \mathbb(N)%% та %%\lim (x_n) = 0%%. Тоді %%f(x_n) = \sin(\left((-1)^nn\pi\right)) \equiv 0%% та %%\lim\big\(f(x_n)\big\) = 0 %%.

Потім візьмемо послідовність, що сходить до тієї ж точки, $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$

для якої %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% і %%\lim\big\(f(x"_n)\big\) = 1%%. Аналогічно для послідовності $$ x""_n = \left\(-\frac(2)((4n + 1) \pi) \right\), $$

також сходить до точки %%x = 0%%, %%\lim\big\(f(x""_n)\big\) = -1%%.

Усі три послідовності дали різні результати, що суперечить умові визначення Гейне, тобто. дана функція немає межі в точці %%x = 0%%.

Теорема

Визначення межі по Коші та Гейні еквівалентні.

Наводяться формулювання основних теорем та властивостей межі функції. Дано визначення кінцевих та нескінченних меж у кінцевих точках та на нескінченності (двосторонніх та односторонніх) по Коші та Гейні. Розглянуто арифметичні властивості; теореми, пов'язані з нерівностями; критерій збіжності Коші; межа складної функції; властивості нескінченно малих, нескінченно великих та монотонних функцій. Дано визначення функції.

Друге визначення щодо Коші

Тут a і x 0 також можуть бути як кінцевими числами, так і віддаленими точками. За допомогою логічних символів існування та загальності це визначення можна записати так:
.

Якщо як безліч взяти ліву або праву околицю кінцевої точки, то отримаємо визначення межі по Коші ліворуч або праворуч.

Теорема
Визначення межі функції по Коші та Гейні еквівалентні.
Доказ

Околиці точок, що застосовуються

Тоді, фактично, визначення Коші означає наступне.
Для будь-яких позитивних чисел , існують числа , так що для всіх x, що належать проколоті околиці точки : , значення функції належать околиці точки a: ,
де , .

З таким визначенням не зовсім зручно працювати, оскільки околиці визначаються за допомогою чотирьох чисел. Але його можна спростити, якщо ввести околиці з рівновіддаленими кінцями. Тобто можна покласти. Тоді ми отримаємо визначення, яке простіше використовувати за доказом теорем. При цьому воно є еквівалентним визначенню, в якому використовуються довільні околиці. Доказ цього факту наводиться у розділі «Еквівалентність визначень межі функції Коші» .

Тоді можна дати єдине визначення межі функції в кінцевих та нескінченно віддалених точках:
.
Тут для кінцевих точок
; ;
.
Будь-які околиці нескінченно віддалених точок є проколотими:
; ; .

Кінцеві межі функції у кінцевих точках

За допомогою логічних символів існування та загальності визначення межі функції можна записати так:
.

Односторонні межі.
Ліва межа в точці (лівостороння межа):
.
Права межа в точці (правостороння межа):
.
Межі ліворуч і праворуч часто позначають так:
; .

Кінцеві межі функції у нескінченно віддалених точках

Аналогічно визначаються межі в нескінченно віддалених точках.
.
.
.

Нескінченні межі функції

Також можна ввести визначення нескінченних меж певних знаків, рівних та :
.
.

Властивості та теореми межі функції

Далі ми вважаємо, що ці функції визначені у відповідній проколоті околиці точки , яка є кінцевим числом або одним із символів: . Також може бути точкою односторонньої межі, тобто мати вигляд або . Околиця є двосторонньою для двосторонньої межі та односторонньою для односторонньої.

Основні властивості

Якщо значення функції f (x)змінити (або зробити невизначеними) у кінцевому числі точок x 1, x 2, x 3, ... x n, то ця зміна ніяк не вплине на існування та величину межі функції у довільній точці x 0 .

Якщо існує кінцева межа, то існує така проколота околиця точки x 0 , на якій функція f (x)обмежена:
.

Нехай функція має у точці x 0 кінцева межа, відмінна від нуля:
.
Тоді, для будь-якого числа c з інтервалу існує така проколота околиця точки x 0 , що для ,
, якщо;
якщо .

Якщо, на деякому проколоті околиці точки , - постійна, то .

Якщо існують кінцеві межі та і на деякому проколоті околиці точки x 0
,
то.

Якщо , і на деякій околиці точки
,
то.
Зокрема, якщо на деякій околиці точки
,
то якщо, то і;
якщо, то і.

Якщо на деякому проколоті околиці точки x 0 :
,
і існують кінцеві (або нескінченні певного знака) рівні межі:
, то
.

Докази основних властивостей наведено на сторінці
"Основні властивості межі функції".

Нехай функції і визначені в деякій проколоті околиці точки. І нехай існують кінцеві межі:
та .
І нехай C – постійна, тобто задане число. Тоді
;
;
;
якщо .

Якщо то .

Докази арифметичних властивостей наведено на сторінці
"Арифметичні властивості межі функції".

Критерій Коші існування межі функції

Теорема
Для того, щоб функція , визначена на деякому проколоті околиці кінцевої або нескінченно віддаленої точки x 0 , мала в цій точці кінцеву межу, необхідно і достатньо, щоб для будь-якого ε > 0 існувала така проколота околиця точки x 0 , Що для будь-яких точок і з цієї околиці, виконувалася нерівність:
.

Межа складної функції

Теорема про межу складної функції
Нехай функція має межу і відображає проколоту околицю точки на проколоту околицю точки. Нехай функція визначена на цьому околиці і має на ній межу.
Тут - кінцеві чи нескінченно віддалені точки: . Околиці та відповідні їм межі можуть бути як двосторонні, і односторонні.
Тоді існує межа складної функції і він дорівнює:
.

Теорема про межу складної функції застосовується у тому випадку, коли функція не визначена у точці або має значення, відмінне від граничного . Для застосування цієї теореми, повинна існувати проколота околиця точки , де безліч значень функції не містить точку :
.

Якщо функція безперервна у точці , то знак межі можна застосовувати до аргументу безперервної функції:
.
Далі наводиться теорема, що відповідає цьому випадку.

Теорема про межу безперервної функції від функції
Нехай існує межа функції g (x)при x → x 0 , і він дорівнює t 0 :
.
Тут точка x 0 може бути кінцевою чи нескінченно віддаленою: .
І нехай функція f (t)безперервна в точці t 0 .
Тоді існує межа складної функції f (g(x)), і він дорівнює f (t 0):
.

Докази теорем наведено на сторінці
«Межа і безперервність складної функції».

Нескінченно малі та нескінченно великі функції

Нескінченно малі функції

Визначення
Функція називається нескінченно малою при , якщо
.

Сума, різницю та твіркінцевого числа нескінченно малих функцій при є нескінченно малою функцією при .

Добуток функції, обмеженоїна деякому проколоті околиці точки, на нескінченно малу при є нескінченно малою функцією при.

Для того, щоб функція мала кінцеву межу, необхідно і достатньо, щоб
,
де - нескінченно мала функція при .

"Властивості нескінченно малих функцій".

Нескінченно великі функції

Визначення
Функція називається нескінченно великою при , якщо
.

Сума або різниця обмеженої функції, на деякому проколоті околиці точки , і нескінченно великий функції при є нескінченно великою функцією при .

Якщо функція є нескінченно великою при , а функція - обмежена, на деякому проколоті околиці точки , то
.

Якщо функція , на деякому проколоті околиці точки , задовольняє нерівності:
,
а функція є нескінченно малою при:
, і (на деякому проколоті околиці точки ), то
.

Докази властивостей викладені у розділі
"Властивості нескінченно великих функцій".

Зв'язок між нескінченно великими та нескінченно малими функціями

З двох попередніх властивостей випливає зв'язок між нескінченно великими та нескінченно малими функціями.

Якщо функція є нескінченно великою при , то функція є нескінченно малою при .

Якщо функція є нескінченно малою при , і , то функція є нескінченно великою при .

Зв'язок між нескінченно малою та нескінченно великою функцією можна виразити символічним чином:
, .

Якщо нескінченно мала функція має певний знак при , тобто позитивна (або негативна) на деякому проколоті околиці точки , то цей факт можна виразити так:
.
Так само якщо нескінченно велика функція має певний знак при , то пишуть:
.

Тоді символічний зв'язок між нескінченно малими та нескінченно великими функціями можна доповнити такими співвідношеннями:
, ,
, .

Додаткові формули, що зв'язують символи нескінченності, можна знайти на сторінці
«Нескінченно віддалені точки та їх властивості».

Межі монотонних функцій

Визначення
Функція , визначена на деякій множині дійсних чисел X називається строго зростаючоюякщо для всіх таких що виконується нерівність:
.
Відповідно, для суворо спадаючоюфункції виконується нерівність:
.
Для невтратною:
.
Для незростаючою:
.

Звідси випливає, що функція, що строго зростає, також є неубутньою. Строго спадна функція також є незростаючою.

Функція називається монотонної, якщо вона незнижена або незростаюча.

Теорема
Нехай функція не зменшується на інтервалі, де.
Якщо вона обмежена зверху числом M:, існує кінцева межа. Якщо не обмежена зверху, то .
Якщо обмежена знизу числом m:, існує кінцева межа. Якщо не обмежена знизу, то .

Якщо точки a і b є нескінченно віддаленими, то виразах під знаками меж мається на увазі, що .
Цю теорему можна сформулювати компактніше.

Нехай функція не зменшується на інтервалі, де. Тоді існують односторонні межі в точках a і b:
;
.

Аналогічна теорема для функції, що не зростає.

Нехай функція не зростає на інтервалі, де. Тоді існують односторонні межі:
;
.

Доказ теореми викладено на сторінці
"Межі монотонних функцій".

Визначення функції

функцією y = f (x)називається закон (правило), згідно з яким, кожному елементу x множини X ставиться у відповідність один і тільки один елемент y множини Y .

Елемент x ∈ Xназивають аргументом функціїабо незалежної змінної.
Елемент y ∈ Yназивають значенням функціїабо залежною змінною.

Безліч X називається областю визначення функції.
Безліч елементів y ∈ Y, які мають прообрази у множині X , називається областю або безліччю значень функції.

Дійсна функція називається обмеженою зверху (знизу)якщо існує таке число M , що для всіх виконується нерівність:
.
Числова функція називається обмеженоюякщо існує таке число M , що для всіх :
.

Верхньою граннюабо точним верхнім кордономНасправді функції називають найменше з чисел, що обмежує область її значень зверху. Тобто це таке число s, для якого для всіх і для будь-якого, знайдеться такий аргумент, значення функції якого перевищує s′:.
Верхня грань функції може позначатися так:
.

Відповідно нижньою граннюабо точним нижнім кордономНасправді функції називають найбільше з чисел, що обмежує область її значень знизу. Тобто це таке число i , для якого для всіх і для будь - якого , знайдеться такий аргумент , значення функції якого менше ніж i : .
Нижня грань функції може позначатися так:
.

Використана література:
Л.Д. Кудрявці. Курс математичного аналізу. Том 1. Москва, 2003.
С.М. Микільський. Курс математичного аналізу. Том 1. Москва, 1983.