Метод сполучених напрямків. Сполучені напрямки Метод сполучених напрямків c
Подібні документи
Розгляд ефективності застосування методів штрафів, безумовної оптимізації, сполучених напрямів та якнайшвидшого градієнтного спуску для вирішення задачі пошуку екстремуму (максимуму) функції кількох змінних за наявності обмеження рівності.
контрольна робота , доданий 16.08.2010
Аналіз теорем сполучених функцій. Природне перетворення як сімейство морфізмів. Характеристика властивостей рефлективних підкатегорій Ознайомлення з універсальними стрілками. Розгляд особливостей способу побудови сполучених функторов.
курсова робота , доданий 27.01.2013
Методика перетворення обертання та її значення у вирішенні алгебраїчних систем рівнянь. Отримання результуючої матриці. Ортогональні перетворення відображенням. Ітераційні способи з мінімізацією нев'язки. Рішення шляхом поєднаних напрямів.
реферат, доданий 14.08.2009
Методи вирішення систем лінійних алгебраїчних рівнянь, їх характеристика та відмінні риси, особливості та сфери застосування. Структура методу ортогоналізації та методу сполучених градієнтів, їх різновиди та умови, етапи практичної реалізації.
курсова робота , доданий 01.10.2009
Численні методи пошуку безумовного екстремуму. Завдання безумовної мінімізації. Розрахунок мінімуму функції шляхом покоординатного спуску. Вирішення задач лінійного програмування графічним та симплексним методом. Робота із програмою MathCAD.
курсова робота , доданий 30.04.2011
Формування функції Лагранжа, умови Куна та Таккера. Численні методи оптимізації та блок-схеми. Застосування методів штрафних функцій, зовнішньої точки, покоординатного спуску, сполучених градієнтів для зведення завдань умовної оптимізації до безумовної.
курсова робота , доданий 27.11.2012
Математична модель завдання. Вирішення транспортного завдання методом потенціалів. Значення цільової функції. Система, що складається з 7 рівнянь з 8 невідомими. Розв'язання задач графічним методом. Виділення напівплощини, що відповідає нерівності.
контрольна робота , доданий 12.06.2011
Методи знаходження мінімуму функції однієї змінної та функції багатьох змінних. Розробка програмного забезпечення обчислення локального мінімуму функції Хіммельблау методом покоординатного спуску. Пошук мінімуму функції методом золотого перерізу.
курсова робота , доданий 12.10.2009
Вирішення систем лінійних рівнянь алгебри методом простої ітерації. Поліноміальна інтерполяція функції методом Ньютона із розділеними різницями. Середньоквадратичне наближення функції. Чисельне інтегрування функцій шляхом Гауса.
курсова робота , доданий 14.04.2009
Основні відомості про симплекс-метод, оцінка його ролі та значення у лінійному програмуванні. Геометрична інтерпретація та алгебраїчний сенс. Знаходження максимуму та мінімуму лінійної функції, особливі випадки. Розв'язання задачі матричним симплекс-методом.
Метод орієнтований вирішення завдань із квадратичними цільовими функціями і полягає в фундаментальних теоретичних результатах. Хоча алгоритми, що використовуються в реальних ситуаціях, є ефективними для квадратичних цільових функцій, можуть погано працювати при більш складних цільових функціях, проте цей підхід є цілком розумним.
Визначення. Нехай – симетрична матриця порядку  . Вектори
. Вектори  називаються
називаються  - пов'язаними, якщо вони лінійно незалежні та виконується умова
- пов'язаними, якщо вони лінійно незалежні та виконується умова  при
при  .
.
приклад.Розглянемо функцію
Як матриця  можна взяти матрицю Гессе
можна взяти матрицю Гессе
 .
.
Як один з напрямків виберемо  . Тоді напрямок
. Тоді напрямок  має задовольняти рівність
має задовольняти рівність
 .
.
Слід зазначити, що пов'язані напрями вибираються неоднозначно. Проте якщо додати умову нормування, їх можна визначити однозначно:
Твердження. Будь-яка квадратична функція  змінних, що має мінімум, може бути мінімізована за
змінних, що має мінімум, може бути мінімізована за  кроків, за умови, що пошук ведеться вздовж пов'язаних щодо матриці Гессе напрямків.
кроків, за умови, що пошук ведеться вздовж пов'язаних щодо матриці Гессе напрямків.
Довільна функція може бути досить добре представлена на околиці оптимальної точки її квадратичної апроксимацією. Тому сполучені напрямки можуть бути корисними для її оптимізації. Однак потрібно більш ніж  кроків. Для визначення сполучених напрямків застосовується спосіб, що базується на наступному затвердженні.
кроків. Для визначення сполучених напрямків застосовується спосіб, що базується на наступному затвердженні.
Твердження. Нехай задана квадратична функція  , дві довільні точки
, дві довільні точки  та напрямокS..Якщо точка
та напрямокS..Якщо точка  є точкою мінімуму функції
є точкою мінімуму функції  вздовж напрямкуSз точки
вздовж напрямкуSз точки  , а
, а  - точкою мінімуму функції вздовж напрямкуSз точки
- точкою мінімуму функції вздовж напрямкуSз точки  , то напрям
, то напрям  пов'язано з напрямкомS.
пов'язано з напрямкомS.
Алгоритм
Крок 1.Задати початкову точку  та систему
та систему  лінійно незалежних напрямків
лінійно незалежних напрямків  (Вони спочатку можуть збігатися з напрямками координатних осей).
Мінімізувати функцію
(Вони спочатку можуть збігатися з напрямками координатних осей).
Мінімізувати функцію  при послідовному русі по
при послідовному русі по  напрямки; використовуючи якийсь одномірний пошук; і отриману раніше точку мінімуму взяти як вихідну.
напрямки; використовуючи якийсь одномірний пошук; і отриману раніше точку мінімуму взяти як вихідну.
Крок 2Виконати додатковий крок  , що відповідає повному переміщенню на кроці 1. Обчислити точку
, що відповідає повному переміщенню на кроці 1. Обчислити точку  (Рис 12). Перевірити критерій (*) увімкнення нового напряму в систему сполучених напрямків.
(Рис 12). Перевірити критерій (*) увімкнення нового напряму в систему сполучених напрямків.
Крок 3Нехай  – найбільше зменшення цільової функції у одному з напрямів
– найбільше зменшення цільової функції у одному з напрямів  :
:

і  є напрямком, що відповідає
є напрямком, що відповідає  .
.
Якщо виконуються умови
 (*)
(*)
то пошук продовжити вздовж початкових напрямків  з точки
з точки  або
або  (З тієї точки, де менше значення функції).
(З тієї точки, де менше значення функції).

Крок 4Якщо
умови  не виконуються, то мінімізувати функцію
не виконуються, то мінімізувати функцію  вздовж напрямку
вздовж напрямку  . Точку цього мінімуму взяти як початкову на наступному етапі. На цьому етапі використовувати систему напрямків
. Точку цього мінімуму взяти як початкову на наступному етапі. На цьому етапі використовувати систему напрямків
тобто. напрямок  замінити на
замінити на  , яке помістити в останній стовпець матриці напрямків.
, яке помістити в останній стовпець матриці напрямків.
Крок 5.Якщо  , то мінімум знайдено. Інакше виконайте крок 1.
, то мінімум знайдено. Інакше виконайте крок 1.
приклад.Клацнувши по значку, відкриється Mathcad документ методу сполучених напрямків, у якому можна виконати обчислення.


Мінімізація функції
методом сполучених напрямків
Може здатися нераціональним відкидати найвдаліший напрямок поточної ітерації та встановлювати новий перспективний напрямок на останнє місце замість першого. Однак неважко бачити, що найвдаліший напрямок швидше за все вичерпав себе, а новий перспективний напрямок щойно було використано для одномірної оптимізації і застосовувати його відразу ж немає жодного сенсу, оскільки просування просто не буде.
Пауелл довів, що визначник матриці напрямків набуває максимального значення тоді і тільки тоді, коли напрямки  ,
, пов'язані щодо матриці Гессе. Він дійшов висновку, що напрямок повного переміщення має замінювати попереднє лише у тому випадку, коли цей напрямок збільшує визначник матриці напрямків, оскільки тільки тоді новий набір напрямків буде ефективним.
пов'язані щодо матриці Гессе. Він дійшов висновку, що напрямок повного переміщення має замінювати попереднє лише у тому випадку, коли цей напрямок збільшує визначник матриці напрямків, оскільки тільки тоді новий набір напрямків буде ефективним.
Доведено, що процедура Пауелла сходить до точки, в якій градієнт дорівнює нулю, якщо цільова функція випукла. Ця точка є локальним мінімумом. Метод дуже чутливий до способу побудови пов'язаних напрямків і тому залежить від точності використовуваного одновимірного пошуку. Пауелл запропонував використати послідовність квадратичних інтерполяцій зі спеціальною процедурою налаштування параметрів цього лінійного пошуку. Проте чисельні дослідження показали, що метод сполучених напрямів Пауелла не слід використовувати за розмірності понад 20.
Методи якнайшвидшого спуску та спуску по координатах навіть для квадратичної функції вимагають нескінченного числа ітерацій. Однак можна побудувати такі напрямки спуску, що для квадратичної функції
- (3.12)
- (Де r є n-мірний вектор) з симетричною позитивно визначеною матрицею А процес спуску зійдеться точно до мінімуму за кінцеве число кроків.
Позитивно певна матриця дозволяє ввести норму вектора таким чином:
Визначення (3.13) означає, що під скалярним твором двох векторів x і тепер розуміється величина (х, Ау). Вектори, ортогональні у сенсі цього скалярного твору
(х, Ау) = 0 (3.14)
називають сполученими (стосовно даної матриці А).
На цьому заснована велика група методів: сполучених градієнтів, сполучених напрямків, паралельних дотичних та інші.
Для квадратичної функції вони використовуються з однаковим успіхом. На довільні функції добре узагальнюється метод сполучених напрямів, у якого деталі алгоритму ретельно відібрані.
Спочатку розглянемо, як цей метод застосовується до квадратичної формі (3.12). Для цього нам потрібні деякі властивості сполучених векторів.
Нехай є деяка система попарно сполучених векторів х i. Нормуємо кожен із цих векторів у сенсі норми (3.14), тоді співвідношення між ними набудуть вигляду
Доведемо, що взаємно пов'язані вектори лінійно-незалежні. З рівності
що суперечить позитивній визначеності матриці. Це протиріччя доводить наше твердження. Отже, система n-сполучених векторів є базисом у n-мірному просторі. Для даної матриці є безліч базисів, що складаються з взаємно пов'язаних векторів.
Нехай знайшли деякий спряжений базис х i , 1 in. Виберемо довільну точку r0. Будь-який рух із цієї точки можна розкласти по сполученому базису

Підставляючи цей вираз у праву частину формули (3.12), перетворимо її з урахуванням сполученості базису (3.15) до наступного виду:
Остання сума складається з членів, кожен з яких відповідає лише одному компоненту суми (3.16). Це означає, що рух по одному зі сполучених напрямків х i змінює лише один член суми (3.17), не торкаючись інших.
Зробимо з точки r 0 почергові спуски до мінімуму по кожному зі сполучених напрямків x i . Кожен спуск мінімізує свій член суми (3.17), тому мінімум квадратичної функції точно досягається після виконання одного циклу спусків, тобто за кінцеве число дій.
Сполучений базис можна побудувати методом паралельних дотичних площин.
Нехай деяка пряма паралельна вектору х, а квадратична функція досягає цієї прямої мінімального значення в точці r 0 . Підставимо рівняння цієї прямої r = r 0 + бx у вираз (3.12) і вимагатимемо виконання умови мінімуму функції
ц(б) = Ф(r 0) + б 2 + б (x, 2Аr 0 + b),
і покладемо (dц/dб) б-0 = 0. Звідси випливає рівняння, якому задовольняє точка мінімуму:
(х, 2Аr 0 + b) = 0. (3.18)
Нехай на якійсь іншій прямій, паралельно першій, функція набуває мінімального значення в точці r 1 ; тоді аналогічно знайдемо (х, 2Аr 1 + b) = 0. Віднімаючи цю рівність з (3.18), отримаємо
(х, А(r 1 r 0)) = 0. (3.19)
Отже, напрям, що з'єднує точки мінімуму на двох паралельних прямих, пов'язане з напрямом цих прямих.
Таким чином, завжди можна побудувати вектор, пов'язаний з довільним заданим вектором х. Для цього достатньо провести дві прямі, паралельні х і знайти на кожній прямій мінімум квадратичної форми (3.12). Вектор r 1 r 0 сполучає ці мінімуми, пов'язаний х. Зауважимо, що пряма стосується лінії рівня у тій точці, де функція на даній прямій набуває мінімального значення; із цим пов'язана назва способу.
Нехай є дві паралельні m-вимірні площини, породжені системою сполучених векторів х i , 1 imn. Нехай квадратична функція досягає свого мінімального значення цих площинах відповідно в точках r 0 і r 1 . Аналогічними міркуваннями можна довести, що вектор r 1 r 0 з'єднує точки мінімуму, пов'язаний з усіма векторами х i . Отже, якщо задана неповна система сполучених векторів х i то цим способом завжди можна побудувати вектор r 1 r 0 , пов'язаний всім векторам цієї системи.
Розглянемо один цикл процесу побудови сполученого базису. Нехай вже побудований базис, у якому останні m векторів взаємно пов'язані, а перші n-m векторів не пов'язані останнім. Знайдемо мінімум квадратичної функції (3.12) у якійсь m-мірній площині, породженій останніми mвекторами базису. Оскільки ці вектори взаємно пов'язані, то для цього достатньо довільно вибрати точку r 0 і зробити з неї спуск по черзі з кожного з цих напрямків (до мінімуму). Точку мінімуму у цій площині позначимо через r 1 .
Тепер з точки r 1 зробимо почерговий спуск за першими n - m векторами базису. Цей спуск виведе траєкторію з першої площини та приведе її до певної точки r 2 . З точки r 2 знову зробимо за останніми напрямками m спуск, який приведе в точку r 3 . Цей спуск означає точне знаходження мінімуму у другій площині, паралельній першій площині. Отже, напрямок r 3 - r 1 пов'язане з останніми m векторами базису.
Якщо одне з несопряженных напрямів у базисі замінити напрямом r 3 - r 1 , то новому базисі вже m + 1 напрям буде взаємно пов'язане.
Почнемо розрахунок циклів із довільного базису; йому вважатимуться, що m=1. Описаний процес за цикл збільшує на одиницю число сполучених векторів у базисі. Отже, за n - 1 цикл усі вектори базису стануть сполученими, і наступний цикл приведе траєкторію до точки мінімуму квадратичної функції (3.12).
Хоча поняття сполученого базису визначено лише для квадратичної функції, описаний вище процес побудований так, що його можна формально застосовувати для довільної функції. Вочевидь, що у своїй шукати мінімум вздовж напрями треба шляхом парабол, не використовуючи ніде формул, що з конкретним видом квадратичної функції (3.12).
У малій околиці мінімуму збільшення досить гладкої функції зазвичай представило у вигляді симетричної позитивно визначеної квадратичної форми типу (3.2). Якби це уявлення було точним, то спосіб сполучених напрямів сходився б за кінцеве число кроків. Але уявлення приблизно, тому число кроків буде нескінченним; Проте збіжність цього методу поблизу мінімуму буде квадратичною.
Завдяки квадратичній збіжності метод сполучених напрямків дозволяє знаходити мінімум із високою точністю. Методи з лінійною збіжністю зазвичай визначають екстремальні значення координат менш точно.
Метод сполучених напрямів є, мабуть, найефективнішим методом спуску. Він непогано працює і при виродженому мінімумі, і при розв'язних ярах, і за наявності слабо похилих ділянок рельєфу - «плато», і за великої кількості змінних - до двох десятків.
СПОРУЖЕНІ НАПРЯМКИ
Пара напрямків, що виходять з точки Рповерхні Sі таких, що їх прямі є сполученими діаметрами індикатриси Дюпена поверхні Sвточці Р.Для того щоб напрямки ( du:dv), вточці Рповерхні Sбули С. н., необхідно і достатньо виконання умови
де L, Мі N -коефіцієнти другої квадратичної форми поверхні S,обчислені у точці Р.Приклади: асимптотичні напрями, основні напрями.
Літ.: Погорєлов А. Ст, Диференціальна, 5 видавництво, М., 1969.
Є. В. Шикін.
Математична енциклопедія. - М: Радянська енциклопедія. І. М. Виноградов. 1977-1985.
Дивитися що таке "СПОРУЖЕНІ НАПРЯМКИ" в інших словниках:
Розділ геометрії, в якому вивчаються геометрич. образи, насамперед криві та поверхні, методами математич. аналізу. Зазвичай у Д. р. вивчаються властивості кривих і поверхонь у малому, тобто властивості скільки завгодно малих їх шматків. Крім того, у … Математична енциклопедія
1) Сума квадратів довжин сполучених півдіаметрів еліпса є величина постійна, що дорівнює сумі квадратів довжин його півосей. 2) Площа описаного навколо еліпса паралелограма, сторони якого мають пов'язані напрямки, постійна і дорівнює ... Математична енциклопедія
Напрямок на регулярній поверхні, крім кривизна нормального перерізу поверхні дорівнює нулю. Для того, щоб напрям у точці Рбуло А. н., необхідно і достатньо виконання умови: де внутрішні координати на поверхні, а L, М і N. Математична енциклопедія
Численні методи розділу обчислювальної математики, присвячений математику. опису та дослідження процесів чисельного розв'язання задач лінійної алгебри. Серед завдань Л. а. Найбільше значення мають дві: рішення системи лінійних алгебраїч. рівнянь… … Математична енциклопедія
Мережа ліній на поверхні, утворена двома сімействами ліній такими, що в кожній точці поверхні лінії мережі різних сімейств мають пов'язані напрямки. Якщо координатна мережа є С. с., то коефіцієнт М другої квадратичної форми. Математична енциклопедія
З 34.21.308-2005: Гідротехніка. Основні поняття. терміни та визначення- Термінологія З 34.21.308 2005: Гідротехніка. Основні поняття. Терміни та визначення: 3.10.28 аванпорт: Обмежена хвилезахисними дамбами акваторія у верхньому б'єфі гідровузла, забезпечена причальними пристроями та призначена для розміщення … Словник-довідник термінів нормативно-технічної документації
I I. Історія розвитку залізниць. Ж. дорога, у тому вигляді, в якому вона існує тепер, винайдено не відразу. Три елементи, її складові, рейковий шлях, перевізні засоби та рухова сила пройшли кожну окрему стадію розвитку. Енциклопедичний словник Ф.А. Брокгауза та І.А. Єфрона
Заробітня плата- (Wages) Найважливіший засіб підвищення зацікавленості працівників Участь трудящих у частці новостворених матеріальних і духовних благ Зміст Зміст. > вести - це найважливіший засіб підвищення зацікавленості… … Енциклопедія інвестора
Диверсифікація- (Diversification) Диверсифікація це інвестиційний підхід спрямований на зниження фінансових ринків Поняття, основні методи та цілі диверсифікації виробництва, бізнесу та фінансових ризиків на валютних, фондових та сировинних ринках Зміст… Енциклопедія інвестора
XIII. Справи внутрішні (1866-1871). 4 го квітня 1866 року, о четвертій годині дня, Імператор Олександр, після звичайної прогулянки в Літньому саду, сідав у візок, коли невідома людина вистрілила в нього з пістолета. У цю хвилину, що стояв у ... Велика біографічна енциклопедія
Крок 1. Задати початкову точку х(0) та систему Nлінійно незалежних напрямків; можливий випадок, коли s(i) = e(i) i = 1, 2, 3,..., N.
Крок 2. Мінімізувати f(x)при послідовному русі ( N+1) напрямкам; при цьому отримана раніше точка мінімуму береться як вихідна, а напрямок s(N)використовується як за першому, і останньому пошуку.
Крок 3. Визначити новий сполучений напрямок за допомогою узагальненої властивості паралельного підпростору.
Крок 4. Замінити s(l) на s(2) і т. д. Замінити s (N)пов'язаним напрямком. Перейти до кроку 2.
Для того, щоб застосувати викладений метод на практиці, його необхідно доповнити процедурами перевірки збіжності та лінійної незалежності системи напрямків. Перевірка лінійної незалежності особливо важлива у випадках, коли функція f(x)не є квадратичною.
З способу побудови алгоритму випливає, що у випадку, коли цільова функція квадратична і має мінімум, точка мінімуму перебуває в результаті реалізації Nциклів, що включають кроки 2, 3 та 4, де N- Кількість змінних. Якщо ж функція не є квадратичною, то потрібно більш ніж Nциклів. Разом з тим, можна дати суворий доказ того, що при деякому припущенні метод Пауелла сходиться до точки локального мінімуму. суперлінійнийшвидкістю (див. дане нижче визначення).
Швидкість збіжності. Розглянутий метод дозволяє побудувати послідовність точок х (k),яка сходиться до рішення x*.Метод називається схожим,якщо нерівність
≤ 1, де (3.39)
= x - х *, (3.40)
виконується кожної ітерації. Оскільки під час розрахунків зазвичай оперують кінцевими десятковими дробами, навіть найефективніший алгоритм вимагає проведення нескінченної послідовності ітерацій. Тому насамперед інтерес представляють асимптотичні властивості збіжності методів, що вивчаються. Говоритимемо, що алгоритм має збіжність порядку r(див. ), якщо
 , (3.41)
, (3.41)
де З- Постійна величина. З формули (3.39) випливає, що за r= 1має місце нерівність З ≤ 1. Якщо r= 1або r= 2, то алгоритм характеризується лінійноїабо квадратичною швидкістю збіжностівідповідно. При r= 1і З= 0 алгоритм характеризується суперлінійнийшвидкістю збіжності.
Приклад 3.6. Метод сполучених напрямків Пауелла
Знайти точку мінімуму функції
f(x) = 2x + 4x x – 10x x+ x,
якщо задана початкова точка х(0) = T , в якій f(x (0)) = 314.
Крок 1. s(1) = T , s(2) = T.
Крок 2. (а) Знайдемо таке значення λ, за якого
f (x (0) + λ s(2)) → min.
Отримаємо: λ* - 0,81, звідки
x(l) = T - 0,81 T = T, f(x(l)) = 250.
(б) Знайдемо таке значення λ, за якого f (x(1) + λ s(1)) → min.
λ* = – 3,26, x (2) = T,f(x (2)) = 1.10.
(в) Знайдемо таке значення λ, за якого f (x(2) + λ s(2)) → min.
λ* = – 0.098, x (3) = T,f(x (3)) = 0.72.
Крок 3. Покладемо s (3) = х (3) - x (1) = [-3.26,-0.098]T. Після нормування отримаємо
s (3) = = [– 0,99955, – 0,03]T.
Покладемо s(1) = s(2) , s(2) = s(3) і перейдемо до кроку 2 алгоритму.
Крок 4. Знайдемо таке значення λ, за якого f (x(3) + λ s(2)) → min.
λ* = – 0.734, x (4) = T,f(x (4)) = – 2,86.
Примітка.Якби f(x)була квадратичною функцією, то отримана точка була вирішенням завдання (якщо знехтувати помилкою округлення). У разі ітерації слід продовжити до отримання рішення.
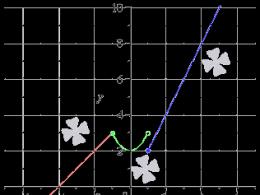
Напрямки пошуку, отримані у процесі реалізації методу, показано на рис. 3.13.
Результати обчислювальних експериментів дозволяють стверджувати, що метод Пауелла (доповнений процедурою перевірки лінійної залежності напрямів) відрізняється щонайменше так само високою надійністю, як і інші методи прямого пошуку, і в ряді випадків є значно ефективнішим. Тому проблема вибору алгоритму прямого пошуку часто (і обґрунтовано) вирішується на користь методу Пауелла.
Тут закінчується розгляд методів прямого пошуку рішень на завдання безумовної оптимізації. У наступному розділі описуються методи, що ґрунтуються на використанні похідних.
Градієнтні методи
У попередньому розділі розглядалися методи, що дозволяють отримати розв'язання задачі на основі використання лише значень цільової функції. Важливість прямих методів безсумнівна, оскільки у ряді практичних інженерних завдань інформація про значення цільової функції є єдиною надійною інформацією, яку має дослідник.
f(x) = 2x + 4x x – 10x x+ x

Рис. 3.13. Розв'язання задачі з прикладу 3.6 методом сполучених напрямків Пауелла.
З іншого боку, при використанні найефективніших прямих методів для отримання рішення іноді потрібна надзвичайно велика кількість обчислень значень функції. Ця обставина поряд із цілком природним прагненням реалізувати можливості знаходження стаціонарних точок [т. е. точок, що задовольняють необхідній умові першого порядку (3.15а)] призводить до необхідності розгляду методів, що ґрунтуються на використанні градієнта цільової функції. Зазначені методи носять ітеративний характер оскільки компоненти градієнта виявляються нелінійними функціями керованих змінних.
Далі скрізь передбачається, що f(х), f(x)і f(x)існують і безперервні. Методи з використанням як перших, так і других похідних розглядаються лише коротко і головним чином у зв'язку з більш корисними методами. Особлива увага приділяється докладному викладу методів сполучених градієнтів,в основі яких лежить введене вище поняття сполученості напрямів, і про квазиньютоновских методів, які аналогічні методу Ньютона, але використовують лише інформацію про перших похідних. Передбачається, що компоненти градієнта можуть бути записані в аналітичному вигляді або з високою точністю обчислені за допомогою чисельних методів. Крім того, розглядаються способи чисельної апроксимації градієнтів.
x = x +α s(x) (3.42)
де x -поточне наближення до рішення х *; α - Параметр характеризує довжину кроку; s(x) = s -напрямок пошуку в N-мірномупросторі керованих змінних x i , i = 1, 2, 3,..., N.Спосіб визначення s(x)та α на кожній ітерації пов'язаний з особливостями методу, що застосовується. Зазвичай вибір α здійснюється шляхом вирішення задачі мінімізації f(x)в напрямку s(x). Тому при реалізації методів, що вивчаються, необхідно використовувати ефективні алгоритми одновимірної мінімізації.
3.3.1. Метод Коші
Припустимо, що у певній точці простору керованих змінних потрібно визначити напрямок якнайшвидшого локального спуску, тобто найбільшого локального зменшення цільової функції. Як і раніше, розкладемо цільову функцію на околиці точки у ряд Тейлора
f(x) = f()+ f() ∆x+… (3.43)
і відкинемо члени другого порядку та вище. Неважко бачити, що локальне зменшення цільової функції визначається другим доданком, оскільки значення f()фіксовано. Найбільше зменшення fасоціюється з вибором такого напрямку (3.42), якому відповідає найбільша негативнавеличина скалярного твору, що фігурує як другий доданок розкладання. З якості скалярного твору випливає, що зазначений вибір забезпечується при
s() = – f(),(3.44)
і другий доданок набуде вигляду
–α f() f().
Розглянутий випадок відповідає якнайшвидшому локальному спуску. Тому в основі найпростішого градієнтного методулежить формула
x = x –α f(x), (3.45)
де - заданий позитивний параметр. Метод має два недоліки: по-перше, виникає необхідність вибору відповідного значення α , і, по-друге, методу властива повільна збіжність до точки мінімуму внаслідок малості fна околиці цієї точки.
Таким чином, доцільно визначати значення α на кожній ітерації
x = x –α f(x), (3.46)
Значення α обчислюється шляхом вирішення задачі мінімізації f (x(k +1)) вздовж напрямку f(x) за допомогою того чи іншого методу одновимірного пошуку. Розглянутий градієнтний метод носить назву методу якнайшвидшого спуску, або методу Коші,оскільки Коші першим використовував аналогічний алгоритм на вирішення систем лінійних рівнянь.
Пошук уздовж прямої відповідно до формули (3.46) забезпечує більш високу надійність методу Коші порівняно з найпростішим градієнтним методом, проте швидкість його збіжності при вирішенні низки практичних завдань залишається неприпустимо низькою. Це цілком зрозуміло, оскільки зміни змінних безпосередньо залежать від величини градієнта, яка прагне нуля в околиці точки мінімуму, і немає механізму прискорення руху до точки мінімуму на останніх ітераціях. Одна з головних переваг методу Коші пов'язана із його стійкістю. Метод має важливу властивість, яка полягає в тому, що при досить малій довжині кроку ітерації забезпечують виконання нерівності
f (x) ≤ f (x). (3.47)
З урахуванням цієї властивості зауважимо, що метод Коші, як правило, дозволяє істотно зменшити значення цільової функції під час руху з точок, розташованих на значних відстанях від точки мінімуму, і тому часто використовується при реалізації градієнтних методів як початкова процедура. Нарешті, з прикладу методу Коші можна продемонструвати окремі прийоми, які застосовуються при реалізації різних градієнтних алгоритмів.
Приклад 3.7. Метод Коші
Розглянемо функцію
f(x) = 8x + 4x x + 5x
та використовуємо метод Коші для вирішення задачі її мінімізації.
Рішення. Насамперед обчислимо компоненти градієнта
= 16x + 4x, = 10x + 4x.
Для того щоб застосувати метод якнайшвидшого спуску, поставимо початкове наближення
x (0) = T
і за допомогою формули (3.46) збудуємо нове наближення
x = x-α f(x)
f(x) = 8x + 4x x + 5x

Рис. 3.14. Ітерації методом Коші з допомогою методу квадратичної інтерполяції.
Таблиця 3.1.Результати обчислень за методом Коші
| k | x | x | f(x) |
| 1 | -1.2403 | 2.1181 | 24.2300 |
| 2 | 0.1441 | 0.1447 | 0.3540 |
| 3 | -0.0181 | 0.0309 | 0.0052 |
| 4 | 0.0021 | 0.0021 | 0.0000 |
Виберемо α таким чином, щоб f (x(1)) → min.; α = 0,056. Отже, x (1) = [– 1,20, 2.16]TДалі знайдемо точку
x = x –α f(x),
обчисливши градієнт у точці xі провівши пошук вздовж прямої.
У таблиці 3.1 представлені дані, отримані під час проведення ітерацій з урахуванням одномірного пошуку методом квадратичної інтерполяції . Послідовність отриманих точок зображено на рис. 3.14.
Незважаючи на те, що метод Коші не має великого практичного значення, він реалізує найважливіші кроки більшості градієнтних методів. Блок-схема алгоритму Коші наведено на рис. 3.15. Зауважимо, що робота алгоритму завершується, коли модуль градієнта або модуль вектора ∆xстає досить малим.

Рис. 3.15. Блок-схема методу Коші.
3.3.2. Метод Ньютона
Неважко бачити, що в методі Коші застосовується найкраща локальна стратегія пошуку з використанням градієнта. Однак рух у напрямку, протилежному градієнту, приводить в точку мінімуму лише в тому випадку, коли лінії рівня функції fявляють собою кола. Таким чином, напрям, протилежний градієнту, взагалі кажучи, неможе бути прийнятним глобальнимнапрямом пошуку точок оптимуму нелінійних функцій. Метод Коші ґрунтується на послідовній лінійній апроксимації цільової функції та вимагає обчислення значень функції та її перших похідних на кожній ітерації. Щоб побудувати більш загальну стратегію пошуку, слід залучити інформацію про другі похідні цільової функції.
Знову розкладемо цільову функцію в ряд Тейлора
f(x)=f(x)+ f(x ) ∆x+½∆x f(x )∆x+O(∆x³).
Відкидаючи всі члени розкладання третього порядку та вище, отримаємо квадратичну апроксимацію f(x):
(x; x) = f(x) + f(x ) T ∆x + ½∆x f(x )∆x,(3.48)
де (x; x)- апроксимуюча функціязмінної х,побудована у точці x.На основі квадратичної апроксимації функції f(х)сформуємо послідовність ітерацій таким чином, щоб у точці, що знову одержується. xградієнт апроксимуючоюфункції звертався на нуль. Маємо
(x; x) = + f(x)+ f(x) = 0, (3.49)