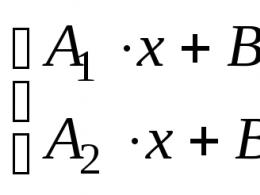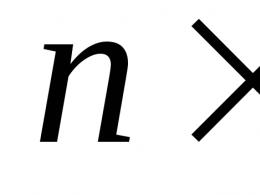Проекція точки на пряму координати проекції точки на пряму. Проекція точки на пряму, координати проекції точки на пряму Спроектувати точку на пряму x y z

1-12. Проекція точки на площину чи пряму

ПОСТАНОВКА ЗАДАЧІ.Знайти координати проекції Р" точки P(^PiУРЧzp) па площину Ах + By -\- Cz-\- D = О,

ПЛАН РІШЕННЯ. Проекція Р точки Р на площину є підставою перпендикуляра, опущеного з точки Р на цю площину.

1. Складаємо рівняння прямої, що проходить через точку Р пер пендикулярно даній площині. Для цього як напрямний вектор прямий беремо нормальний вектор площини: а = п = = (А, В, С). Тоді канонічні рівняння прямої мають вигляд

X = At-\-хр, у = Bt-\-yp, Z=z Ct-\-Zp.

3. Підставляючи x^y^z у рівняння площини та вирішуючи його щодо t, знаходимо значення параметра t = to, при якому відбувається перетин прямої та площини.

4. Знайдене значення ^о підставляємо в параметричні рівняння прямої і одержуємо шукані координати точкиР".

ЗАУВАЖЕННЯ. Аналогічно вирішується задача про знаходження координат проекції точки на пряму.

ПРИКЛАД. Знайти координати проекції Р точки Р(1,2,-1) на площину Зж - 2/4-22: - 4 = 0.

1. Складаємо рівняння прямої, що проходить через точку Р пер пендикулярно даній площині. Для цього як напрямний вектор прямий беремо нормальний вектор площини: а = п =

3. Підставляючи ці вирази для х^ у і z до рівняння площини, знаходимо значення параметра ^, при якому відбувається перетин прямий та площини:

3(3t + 1) – l(-t + 2) + 2(2t – 1) – 27 = О = > to = 2.

4. Підставляючи параметричні рівняння прямий знайдене значення to = 2, отримуємо жо = 7, уо = О, ^о = 1.

Таким чином, точка перетину прямої та площини і, отже, проекція точки Р на площину має координати (7,0,1).

Відповідь. Проекція Р має координати (7,0,1).

Відповіді. 1.(2,3/2,2). 2. (-3/2,-3/2,-1/2). 3. (2,-1/2,-3/2). 4. (-1/2,1,1). 5. (1,-1/2,-1/2). 6. (3/2,-1/2,0). 7. (1/2,-1,-1/2). 8. (1/2,-1/2,1/2). 9. (1/2,-1/2,1/2). 10. (1,1 / 2,0).

1.13. Симетрія щодо прямої або площини

ПОСТАНОВКА ЗАДАЧІ.Знайти координати точки Q, симетріч

ПЛАН РІШЕННЯ. Шукана точка Q лежить на прямій, перпендикулярній даній і перетинає її в точці Р". Оскільки точка Р " ділить відрізок PQ навпіл, координати залізничного, уд і ZQ ТОЧКИ Q визначаються з умов

її проекції Р" на цю пряму.

1. Знайдемо проекцію крапкиР дану пряму, тобто. точку Р "(див. задачу 1.12). Для цього:

а) складемо рівняння площини, що проходить через точку Р пер пендикулярно даній прямій. В якості нормального вектора цієї площини можна взяти напрямний вектор даної прямий, тобто. п = а = (l^m^n). Отримуємо

1(х - Хр) + т(у - УР) -f n(z - zp) = 0;

б) знайдемо координати точки перетину Р " цієї площини з даною прямою. Для цього запишемо рівняння прямої в параметричній формі

X = Н-\-жо, y = mt-\-yo, Z = nt-\-ZQ.

Підставляючи x^y^z у рівняння площини і вирішуючи його щодо t, знаходимо значення параметра t = to, при якому відбувається перетин прямої та площини;

в) знайдене значення to підставляємо в параметричні рівняння прямої і отримуємо шукані координати точки Р".

2. Координати точки Q, симетричної точки Р щодо даної прямої, визначаємо з умов (1). Отримуємо

XQ = 2хр/ - Хр, yq = 2ур" - ур, ZQ = 22; р/ - zp.

ЗАУВАЖЕННЯ. Аналогічно вирішується задача про знаходження координат точки, симетричної даної, щодо площини.

ПРИКЛАД. Знайти координати точки Q, симетричної точки Р(2, -1,2) щодо прямої

X - 1 _ у __ Z -\-1

РІШЕННЯ.

1. Знайдемо проекцію крапкиР дану пряму, тобто. точку Р". Для цього:

а) складемо рівняння площини, що проходить через точку Р пер пендикулярно даній прямій. В якості нормального вектора цієї площини можна взяти напрямний вектор даної прямої: n = a = (1,0,-2). Тоді

Підставляючи ці вирази для х, у і z рівняння площини, знаходимо значення параметра t, при якому відбувається перетин прямий і площини: to = -1;

в) підставляючи параметричні рівняння прямої знайдене значення to = -1, отримуємо

жр/ = О, г/р/ = О, zpr = 1.

Таким чином, точка перетину прямої та площини і, отже, проекція точки Р на пряму є Р”(0,0,1).

2. Координати точки Q, симетричної точки Р щодо даної прямої, визначаються з умов (1):

XQ = 2хр" - Хр = -2,

VQ = 2ур/ - 2/р = 1,

ZQ = 2zpf – zp = 0.

Відповідь. Крапка Q має координати (-2,1,0).

Умови завдання. Знайти координати точки, симетричній точці Р відносно заданої прямої.

У цій статті спочатку дано визначення проекції точки на пряму (на вісь) і наведено малюнок, що пояснює. Далі розібраний спосіб знаходження координат проекції точки на пряму у введеній прямокутній системі координат на площині та тривимірному просторі, показані рішення прикладів з докладними поясненнями.

Навігація на сторінці.

Проекція точки на пряму – визначення.

Оскільки всі геометричні фігури складаються з точок, а проекція фігури є безліч проекцій всіх точок цієї фігури, то проектування фігури на пряму необхідно вміти проектувати точки цієї фігури цю пряму.

То що називають проекцією точки на пряму?

Визначення.

Проекція точки на пряму- Це або сама точка, якщо вона лежить на даній прямій, або основа перпендикуляра, опущеного з цієї точки на задану пряму.

На наведеному нижче малюнку точка H 1 є проекцією точки M 1 на пряму a, а точка M 2 є проекція самої точки М 2 на пряму a тому, що М 2 лежить на прямій a .

Це визначення проекції точки на пряму справедливе як випадку на площині, так випадку у тривимірному просторі.

На площині, щоб побудувати проекцію точки М 1 на пряму a потрібно провести пряму b яка проходить через точку М 1 і перпендикулярна прямий a . Тоді точка перетину прямих a і є проекцією точки М 1 на пряму a .

У тривимірному просторі проекцією точки М 1 на пряму a є точка перетину прямої a та площини, що проходить через точку М 1 перпендикулярно до прямої a.

Знаходження координат проекції точки на пряму – теорія та приклади.

Почнемо з знаходження координат проекції точки на пряму, коли точка, що проектується, і пряма задані в прямокутній системі координат Oxy на площині. Після цього покажемо, як знаходяться координати проекції точки на пряму прямокутну систему координат Oxyz в тривимірному просторі.

Координати проекції точки прямо на площині.

Нехай на площині зафіксована Oxy, задана точка пряма a і потрібно визначити координати проекції точки М 1 на пряму a.

Розв'яжемо це завдання.

Проведемо через точку М 1 пряму b , перпендикулярну до прямої a , і позначимо точку перетину прямих a і b як H 1 . Тоді H1 – проекція точки М1 на пряму a.

З проведеної побудови логічно випливає алгоритм, що дозволяє знайти координати проекції точки на пряму a:

Розберемося із знаходженням координат проекції точки на пряму при вирішенні прикладу.

приклад.

На площині щодо прямокутної системи координат Oxy задані точка та пряма a , якій відповідає загальне рівняння прямого виду

Рішення.

Рівняння прямої нам відомо з умови, так що можна переходити до другого кроку алгоритму.

Отримаємо рівняння прямої b, яка проходить через точку М1 і перпендикулярна до прямої a. Для цього нам потрібні координати напрямного вектора прямої b. Оскільки пряма b перпендикулярна до прямої a, то нормальний вектор прямої a є напрямним вектором прямої b. Очевидно, нормальним вектором прямий є вектор з координатами , отже, напрямним вектором прямої є вектор . Тепер ми можемо написати канонічне рівняння прямої b, оскільки знаємо координати точки, якою вона проходить, і координати її напрямного вектора: .

Залишилося знайти координати точки перетину прямих a і b, які дадуть шукані координати проекції точки М 1 на пряму a. Для цього спочатку перейдемо від канонічних рівнянь прямої до її загального рівняння: . Тепер складемо систему рівнянь із загальних рівнянь прямих a і b, після чого знайдемо її розв'язання (при необхідності звертайтеся до статті):

Таким чином, проекція точки на пряму має координати.

Відповідь:

приклад.

На площині прямокутної системи координат Oxy задані три точки . Знайдіть координати проекції точки М1 на пряму АВ.

Рішення.

Для знаходження координат проекції точки М 1 на пряму АВ діятимемо за отриманим алгоритмом.

Напишемо рівняння прямої, що проходить через дві задані точки і :
.

Тепер можна від отриманого канонічного рівняння прямої АВ перейти до загального рівняння прямої АВ та продовжити рішення за аналогією з попереднім прикладом. Але давайте розглянемо інший спосіб знаходження рівняння прямої b, що проходить через точку М1 перпендикулярно до прямої АВ.

З канонічного рівняння прямої АВ отримаємо рівняння прямої з кутовим коефіцієнтом: . Кутовий коефіцієнт прямої АВ дорівнює , а кутовий коефіцієнт прямої b , яка перпендикулярна до прямої АВ дорівнює (дивіться умову перпендикулярності прямих). Тоді рівняння прямої b, що проходить через точку і має кутовий коефіцієнт, має вигляд.

Щоб визначити координати проекції точки на пряму АВ, залишилося вирішити систему рівнянь. :

Відповідь:

Давайте ще окремо зупинимося на знаходженні координат проекції точки на координатні прямі Ox і Oy, а також на прямі, паралельні їм.

Очевидно, що проекцією точки на координатну пряму Ox , якій відповідає неповне загальне рівняння прямої виду є точка з координатами . Аналогічно проекція точки на координатну пряму Oy має координати .

Будь-яка пряма, паралельна осі абсцис, може бути задана неповним загальним рівнянням виду , А пряма, паралельна осі ординат, - рівнянням виду . Проекціями точки на прямі є точки з координатами і відповідно.

приклад.

Які координати мають проекції точки на координатну пряму Oy і пряму .

Рішення.

Проекцією точки на пряму Oy є точка з координатами.

Перепишемо рівняння прямої як . Тепер добре видно, що проекція точки прямо має координати .

Відповідь:

І.

Координати проекції точки на пряму у тривимірному просторі.

Тепер переходимо до знаходження координат проекції точки на пряму щодо прямокутної системи координат Oxyz, введеної у тривимірному просторі.

Нехай у просторі зафіксована прямокутна система координат Oxyz, задана точка , Пряма a і потрібно знайти координати проекції точки М 1 на пряму a.

Розв'яжемо це завдання.

Побудуємо площину, яка проходить через точку М1 перпендикулярно до прямої a. Проекцією точки М 1 на пряму a є точка перетину прямої і площини . Таким чином, отримуємо алгоритм, що дозволяє знайти координати проекції точки на пряму a:

Розглянемо рішення прикладу.

приклад.

У прямокутній системі координат Oxyz задана точка та пряма a , причому пряму a визначають канонічні рівняння прямої у просторі виду . Знайдіть координати проекції точки М1 на пряму a.

Рішення.

Для визначення координат проекції точки М 1 на пряму скористаємося отриманим алгоритмом.

Рівняння прямої нам відразу відомі з умови, так що переходимо до другого кроку.

Отримаємо рівняння площини, яка перпендикулярна до прямої і проходить через точку. Для цього нам потрібно знати координати нормального вектора площини. Знайдемо їх. З канонічних рівнянь прямої a видно координати напрямного вектора цієї прямої: . Напрямний вектор прямої є нормальним вектором площини, яка перпендикулярна до прямої a . Тобто, - Нормальний вектор площини. Тоді рівняння площини, що проходить через точку і має нормальний вектор , має вигляд .

Залишилося знайти координати точки перетину прямої a та площини - вони є шуканими координатами проекції точки на пряму a . Покажемо два способи їхнього знаходження.

Перший метод.

З канонічних рівнянь прямої a отримаємо рівняння двох площин, що перетинаються , які визначають пряму a:

Координати точки перетину прямої та площині ми отримаємо, розв'язавши систему лінійних рівнянь виду . Застосуємо (якщо Вам більше подобається або якийсь інший метод розв'язання систем лінійних рівнянь, то застосовуйте його):

Таким чином, точка з координатами є проекцією точки М на пряму a .

Другий спосіб.

Знаючи канонічні рівняння прямої a легко записати її параметричні рівняння прямої в просторі : . Підставимо в рівняння площини виду замість x , y та z їх вираження через параметр:

Тепер ми можемо обчислити шукані координати точки перетину прямої a та площини за параметричними рівняннями прямої a при:

Ця стаття розглядає поняття проекції точки на пряму (вісь). Ми дамо йому визначення з використанням малюнку, що пояснює; вивчимо спосіб визначення координат проекції точки на пряму (на площині або тривимірному просторі); Розберемо приклади.

У статті "Проекція точки на площину, координати" ми згадували, що проектування фігури є узагальненим поняттям перпендикулярного або ортогонального проектування.

Всі геометричні фігури складаються з точок, відповідно проекція цієї фігури є безлічю проекцій усіх її точок. Тому щоб мати можливість спроектувати фігуру на пряму, необхідно отримати навичку проектування точки на пряму.

Визначення 1

Проекція точки на пряму– це або сама точка, якщо вона належить заданій прямій, або основа перпендикуляра, опущеного з цієї точки на задану пряму.

Розглянемо малюнок нижче: точка H 1 служить проекцією точки М 1 на пряму a, а точка М 2 , що належить прямий, є проекцією сама себе.

Дане визначення правильне для випадку на поверхні і в тривимірному просторі.

Щоб на площині отримати проекцію точки М 1 на пряму a проводиться пряма b , що проходить через задану точку M 1 і перпендикулярна прямий a . Таким чином, точка перетину прямих a та b буде проекцією точки М 1 на пряму a .

У тривимірному просторі проекцією точки на пряму буде точка перетину прямої a і площини α, що проходить через точку М 1 і перпендикулярної прямої a .

Знаходження координат проекції точки на пряму

Розглянемо це питання у випадках проектування на площині та у тривимірному просторі.

Нехай нам задані прямокутна система координат O x y, точка М1 (x1, y1) і пряма a. Необхідно знайти координати проекції точки М1 на пряму a.

Прокладемо через задану точку М 1 (x 1 , y 1) пряму b перпендикулярно до прямої a . Точку перетину маркуємо як H1. Точка Н 1 буде точкою проекції точки М 1 на пряму a .

З описаної побудови можна сформулювати алгоритм, який дозволяє знаходити координати проекції точки М 1 (x 1 y 1) на пряму a:

Складаємо рівняння прямої (якщо воно не задано). Для здійснення цієї дії необхідна навичка складання основних рівнянь на площині;

Записуємо рівняння прямої b (що проходить через точку М 1 і перпендикулярної прямої a). Тут допоможе стаття про рівняння прямої, що проходить через задану точку перпендикулярно до заданої прямої;

Визначаємо шукані координати проекції як координати точки перетину прямих a і b. І тому вирішуємо систему рівнянь, складові якої – рівняння прямих a і b .

Приклад 1

На площині O x y задані точки М 1 (1, 0) та пряма a (загальне рівняння – 3 x + y + 7 = 0). Необхідно визначити координати проекції точки М1 на пряму a.

Рішення

Рівняння заданої прямої відоме, тому, згідно з алгоритмом, переходимо до кроку запису рівняння прямої b. Пряма b перпендикулярна прямий a, отже нормальний вектор прямий a служить напрямним вектором прямий b. Тоді напрямний вектор прямий b запишемо як b → = (3, 1). Запишемо і канонічне рівняння прямої b , оскільки нам також задані координати точки М 1 через яку проходить пряма b:

Завершальним кроком визначаємо координати точки перетину прямих a і b. Перейдемо від канонічних рівнянь прямої до загального її рівняння:

x - 1 3 = y 1 ⇔ 1 · (x - 1) = 3 · y ⇔ x - 3 y - 1 = 0

Складемо систему рівнянь із загальних рівнянь прямих a і b і розв'яжемо її:

3 x + y + 7 = 0 x - 3 y - 1 = 0 ⇔ y = - 3 x - 7 x - 3 y - 1 = 0 ⇔ y = - 3 x - 7 x - 3 · (- 3 x - 7 ) - 1 = 0 ⇔ ⇔ y = - 3 x - 7 x = - 2 ⇔ y = - 3 · (- 2) - 7 x = - 2 ⇔ y = - 1 x = - 2

Зрештою, ми отримали координати проекції точки М 1 (1 , 0) на пряму 3 x + y + 7 = 0: (- 2 , - 1) .

Відповідь: (- 2 , - 1) .

Докладніше розглянемо випадок, коли необхідно визначити координати проекції заданої точки на координатні прямі та паралельні їм прямі.

Нехай задані координатні прямі O x і O y, а також точка М 1 (x 1, y 1). Зрозуміло, що проекцією заданої точки на пряму координату O x виду y = 0 буде точка з координатами (x 1 , 0) . Так і проекція заданої точки на координатну пряму O y матиме координати 0 , y 1 .

Будь-яку довільну пряму, паралельну осі абсцис, можна встановити неповним загальним рівнянням B y + C = 0 ⇔ y = - C B , а пряму, паралельну осі ординат - A x + C = 0 ⇔ x = - C A.

Тоді проекціями точки М 1 (x 1, y 1) на прямі y = - C B і x = - C A стануть точки з координатами x 1, - C B і - C A, y 1 .

Приклад 2

Визначте координати проекції точки М 1 (7 , - 5) на координатну пряму O y , а також на пряму, паралельну до прямої O y 2 y - 3 = 0 .

Рішення

Запишемо координати проекції заданої точки на пряму O y: (0 - 5) .

Запишемо рівняння прямої 2 y - 3 = 0 як y = 3 2 . Стає видно, що проекція заданої точки на пряму y = 3 2 матиме координати 7 3 2 .

Відповідь:(0 , - 5) та 7 , 3 2 .

Нехай у тривимірному просторі задані прямокутна система координат O x y z , точка М 1 (x 1 , y 1 , z 1) та пряма a . Знайдемо координати проекції точки М1 на пряму a.

Побудуємо площину α, що проходить через точку М 1 і перпендикулярну до прямої a . Проекцією заданої точки на пряму a стане точка перетину прямої a та площини α. Виходячи з цього, наведемо алгоритм для знаходження координат проекції точки М 1 (x 1 , y 1 , z 1) на пряму a:

Запишемо рівняння прямої а (якщо воно не задано). Для вирішення цього завдання необхідно ознайомитися із статтею про рівняння прямої у просторі;

Складемо рівняння площини ?

Знайдемо шукані координати проекції точки М 1 (x 1 , y 1 , z 1) на пряму a – це будуть координати точки перетину прямої α та площини α (на допомогу – стаття «Координати точки перетину прямої та площини»).

Приклад 3

Задано прямокутну систему координат O x y z , і в ній – точку М 1 (0 , 1 , - 1) і пряму a . Прямий a відповідають канонічні рівняння виду: x + 23 = y - 6 - 4 = z + 11. Визначте координати проекції точки М1 на пряму a.

Рішення

Використовуємо вказаний вище алгоритм. Рівняння прямої відомі, тому перший крок алгоритму пропускаємо. Запишемо рівняння площини α. Для цього визначимо координати нормального вектора площини. Із заданих канонічних рівнянь прямої a виділимо координати напрямного вектора цієї прямої: (3, - 4, 1), який буде нормальним вектором площини α, перпендикулярної прямої a. Тоді n → = (3, - 4, 1) – нормальний вектор площини α. Таким чином, рівняння площини α матиме вигляд:

3 · (x - 0) - 4 · (y - 1) + 1 · (z - (- 1)) = 0 ⇔ 3 x - 4 y + z + 5 = 0

Тепер знайдемо координати точки перетину прямої а та площини α, для цього використовуємо два способи:

1. Задані канонічні рівняння дозволяють отримати рівняння двох площин, що перетинаються, що визначають пряму a:

x + 2 3 = y - 6 - 4 = z + 1 1 ⇔ - 4 · (x + 2) = 3 · (y - 6) 1 · (x + 2) = 3 · (z + 1) 1 · ( y - 6) = - 4 · (z + 1) ⇔ 4 x + 3 y - 10 = 0 x - 3 z - 1 = 0

Щоб знайти точки перетину прямої 4 x + 3 y - 10 = 0 x - 3 z - 1 = 0 і площині 3 x - 4 y + z + 5 = 0 , розв'яжемо систему рівнянь:

4 x + 3 y - 10 = 0 x - 3 z - 1 = 0 3 x - 4 y + z + 5 = 0 ⇔ 4 x + 3 y = 10 x - 3 z = 1 3 x - 4 y + z = - 5

В даному випадку використовуємо метод Крамера, але можна застосувати будь-який зручний:

∆ = 4 3 0 1 0 - 3 3 - 4 1 = - 78 ∆ x = 10 3 0 1 0 - 3 - 5 - 4 1 = - 78 ⇒ x = ∆ x ∆ = - 78 - 78 = 1 ∆ y = 4 10 0 1 1 - 3 3 - 5 1 = - 156 ⇒ y = ∆ y ∆ = - 156 - 78 = 2 ∆ z = 4 3 10 1 0 1 3 - 4 - 5 = 0 ⇒ z = ∆ z ∆ = 0 – 78 = 0

Таким чином, проекцією заданої точки на пряму a є точка з координатами (1 , 2 , 0)

1. На основі заданих канонічних рівнянь легко записати параметричні рівняння прямої у просторі:

x + 2 3 = y - 6 - 4 = z + 1 1 ⇔ x = - 2 + 3 · λ y = 6 - 4 · λ z = - 1 + λ

Підставимо в рівняння площини, що має вигляд 3 x - 4 y + z + 5 = 0 замість x , y і z їх вираження через параметр:

3 · (- 2 + 3 · λ) - 4 · (6 - 4 · λ) + (- 1 + λ) + 5 = 0 ⇔ 26 · λ = 0 ⇔ λ = 1

Обчислимо шукані координати точки перетину прямої a та площини α за параметричними рівняннями прямої a при λ = 1:

x = - 2 + 3 · 1 y = 6 - 4 · 1 z = - 1 + 1 ⇔ x = 1 y = 2 z = 0

Таким чином, проекція заданої точки на пряму a має координати (1, 2, 0)

Відповідь: (1 , 2 , 0)

Наостанок зазначимо, що проекціями точки М 1 (x 1 , y 1 , z 1) на координатні прямі O x , O y і O z будуть точки з координатами (x 1 , 0 , 0) , (0 , y 1 , 0 ) та (0 , 0 , z 1) відповідно.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter