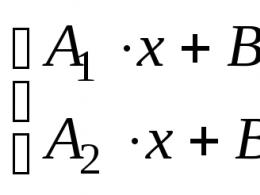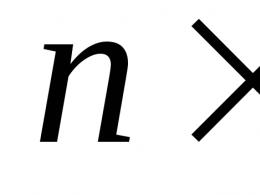Граничні умови першого та другого роду. Кордонні та початкові умови. Коректність постановки граничних умов

Початкові умови

Для можливості відліку змін температури в точках тіла в той чи інший бік у наступні моменти часу має бути заданий початковий термічний стан для його кожної точки. Іншими словами, повинна бути задана безперервна або розривна функція координат Т0 (х, у, z), що повністю описує температурний стан у всіх точках тіла в початковий момент часу t = 0, і потрібна функція Т (х, у, z, t), яка є рішенням диференціального рівняння (1.8), має задовольняти початкову умову

Т (х, у, z, 0i = o = Т0 (х, у, z). (1.11)

Граничні умови

Теплопровідне тіло може бути в різних умовах зовнішнього термічного впливу через його поверхню. Тому з усіх розв'язків диференціального рівняння (1.8) потрібно вибрати те, що відповідає даним умовам на поверхні S, тобто даним конкретним граничним умовам. Використовуються такі форми математичного завдання граничних умов.

1. Температура в кожній точці поверхні тіла може змінюватися з часом за конкретним заданим законом, тобто температура поверхні тіла буде представляти безперервну (або розривну) функцію координат і часу Ts (х, у, z, і). При цьому потрібна функція Т (х, у, z, t), яка є рішенням рівняння (1.8), повинна задовольняти граничну умову

Т (x, y, z, 0 Is = Ts (x, y, z, i). (1.12)

У найпростіших випадках температура поверхні тіла 7 (х, у, z, t) може бути періодичною функцією часу або вона може бути постійною.

2. Відомий потік тепла через поверхню тіла як безперервна (або розривна) функція координат точок поверхні та часу qs (х, у, z, I). Тоді функція Т (х, у, г, I) повинна задовольняти граничну умову:

X grad Т (х, у, z, 0U = Qs (*. У> г> 0-(1 -13))

3. Встановлено температуру навколишнього середовища Та і закон теплообміну між навколишнім середовищем і поверхнею тіла, якою для простоти використовується закон Ньютона. Відповідно до цього закону кількість теплоти dQ, що віддається

за час dt елементом поверхні dS із температурою

Ts (х, у, z, t) у навколишнє середовище, визначається за формулою

dQ = k (Ts – Та) dS dt, (1.14)

де k - коефіцієнт тепловіддачі кал/см2 - сек-°С. З іншого боку, відповідно до формули (1.6), ця кількість тепла підводиться до елемента поверхні зсередини і визначається рівністю

dQ = - х (grad„ 7")s dS dt. (1.15)

Прирівнюючи (1.14) і (1.15), отримаємо, що потрібна функція Т (х, у, z, t) повинна задовольняти граничну умову

(gradnr) s = -±-(Ts-Та). (1.16)

Як зазначалося вище, при стикуванні на монтажі двох секцій конструкції умови для виконання зварювання є найважчими. Виконання зварювання всього перерізу одночасно - абсолютно неможливо, а тому після накладання частини швів.

Якщо загальні деформації зварних конструкцій великий вплив надає послідовність накладання окремих швів, то місцеві деформації і деформації з площини зварюваних листів істотно впливає метод виконання кожного шва. …

Як зазначалося вище, при зварюванні складних складових перерізів і конструкцій характер деформацій, що виникають, залежить від порядку накладання швів. Тому одним із основних засобів боротьби з деформаціями при виготовленні зварних конструкцій.

Одного рівняння руху (1.116) при математичному описі фізичного процесу недостатньо. Потрібно сформулювати умови, достатні для однозначного визначення процесу. При розгляді завдання про коливання струни додаткові умови можуть бути двох видів: початкові та граничні (крайові).

Сформулюємо додаткові умови для струни із закріпленими кінцями. Так як кінці струни довжини закріплені, то їх відхилення в точках і повинні бути рівними нулю при будь-яких :

Умови (1.119) називаються граничнимиумовами; вони показують, що відбувається на кінцях струни протягом процесу коливання.

Очевидно, процес коливань залежатиме від того, яким способом струна виводиться із стану рівноваги. Найзручніше вважати, що струна почала коливатися в момент часу. У початковий момент часу всім точкам струни повідомляються деякі зсуви та швидкості:

,

, ,

(1.120)

де - задані функції.

Умови (1.120) називаються початковимиумовами.

Отже, фізичне завдання про коливання струни звелося до наступного математичного завдання: знайти таке рішення рівняння (1.116) (або (1.117) або (1.118)), яке б задовольняло граничним умовам (1.119) і початковим умовам (1.120). Це завдання називається змішаним крайовим завданням, оскільки включає і граничні і початкові умови. Доведено, що при деяких обмеженнях, накладених на функції і змішана задача має єдине рішення.

Виявляється, що до задачі (1.116), (1.119), (1.120), крім задачі про коливання струни, зводяться інші фізичні завдання: поздовжні коливання пружного стрижня, крутильні коливання валу, коливання рідин і газу в трубі та ін.

Крім граничних умов (1.119), можливі граничні умови інших типів. Найбільш поширеними є такі:

I. , ;

ІІ. , ;

ІІІ. , ,

де , - Відомі функції, а , - Відомі постійні.

Наведені граничні умови називають відповідно граничними умовами першого, другого, третього роду. Умови I мають місце у разі, якщо кінці об'єкта (струна, стрижень тощо.) переміщуються за заданим законом; умови II – у разі, якщо до кінців додано задані сили; умови III – у разі пружного закріплення кінців.

Якщо функції, задані у правій частині рівностей, дорівнюють нулю, то граничні умови називаються однорідними.Так, граничні умови (1.119) – однорідні.

Комбінуючи різні перелічені типи граничних умов, отримаємо шість типів найпростіших крайових завдань.

Для рівняння (1.116) може бути й інше завдання. Нехай струна досить довга і нас цікавить коливання її точок, досить віддалених від кінців, причому протягом малого проміжку часу. У цьому випадку режим на кінцях не надаватиме суттєвого впливу і тому його не враховують; струну ж у своїй вважають нескінченною. Замість повного завдання ставлять граничну задачу з початковими умовами для необмеженої області: знайти рішення рівняння (1.116) для , задовольняє початковим умовам:

, .

), що задає його поведінку в початковий момент часу або на межі області, що розглядається відповідно.

Зазвичай диференціальне рівняння має не одне рішення, а ціле їхнє сімейство. Початкові та граничні умови дозволяють вибрати з нього одне, що відповідає реальному фізичному процесу чи явищу. У теорії звичайних диференціальних рівнянь доведено теорему існування та єдиності розв'язання задачі з початковою умовою (т. зв. задачі Коші). Для рівнянь у приватних похідних отримані деякі теореми існування та єдиності рішень для певних класів початкових та крайових завдань.

Термінологія

Іноді до граничних відносять і початкові умови в нестаціонарних задачах, таких як розв'язання гіперболічних або параболічних рівнянь.

Для стаціонарних завдань існує поділ граничних умов на головніі природні.

Головні умови зазвичай мають вигляд u (∂ Ω) = g (\displaystyle u(\partial \Omega)=g), де ∂ Ω (\displaystyle \partial \Omega )- кордон області Ω (\displaystyle \Omega).

Природні умови містять також і похідну рішення щодо нормалі до кордону.

Приклад

Рівняння d 2 y d t 2 = − g (\displaystyle (\frac (d^(2)y)(dt^(2)))=-g)описує рух тіла на полі земного тяжіння . Йому задовольняє будь-яка квадратична функція виду y (t) = − g t 2 / 2 + a t + b (\displaystyle y(t)=-gt^(2)/2+at+b,)де a, b (\displaystyle a,b)- Довільні числа. Для виділення конкретного закону руху необхідно вказати початкову координату тіла та його швидкість, тобто початкові умови.

Коректність постановки граничних умов

Завдання математичної фізики описують реальні фізичні процеси, тому їх постановка повинна задовольняти наступним природним вимогам:

1. Рішення має існуватиу якомусь класі функцій;
2. Рішення має бути єдиниму якомусь класі функцій;
3. Рішення має безперервно залежати від даних(Початкових та граничних умов, вільного члена, коефіцієнтів тощо).

Вимога безперервної залежності рішення обумовлюється тим обставиною, що фізичні дані, як правило, визначаються з експерименту приблизно, і тому потрібно бути впевненим у тому, що розв'язання задачі в рамках обраної математичної моделі не суттєво залежатиме від похибки вимірювань. Математично цю вимогу можна записати, наприклад, так (для незалежності від вільного члена):

Нехай задано два диференціальні рівняння: L u = F 1 , L u = F 2 (Displaystyle Lu = F_ (1), ~ Lu = F_ (2))з однаковими диференціальними операторами та однаковими граничними умовами, тоді їх рішення безперервно залежатимуть від вільного члена, якщо:

Багато функцій, для яких виконуються перелічені вимоги, називається класом коректності. Некоректну постановку граничних умов добре ілюструє

U| x=0 = g 1 (t), U | x=l = g 2 (t)

Ці умови фізично означають, що у кінцях задані режими коливань.

ІІ. Граничні умови другого роду

U x | x=0 = g 1 (t), U x | x=l = g 2 (t)

Такі умови відповідають з того що на кінцях задані сили.

ІІІ. Граничні умови третього роду

(U x -σ 1 U) | x=0 = g 1 (t) , (U x –σ 2 U) | x=l = g 2 (t)

Ці умови відповідають пружному закріпленню кінців.

Граничні умови (5), (6) та (7) називаються однорідними, якщо праві частини g 1 (t) та g 2 (t) тотожно рівні нулю при всіх значеннях t. Якщо хоча б одна з функцій у правих частинах не дорівнює нулю, то граничні умови називаються неоднорідними.

Аналогічно формулюються граничні умови й у разі трьох чи чотирьох змінних за умови, що з цих змінних - час. Кордоном у цих випадках буде або замкнута крива Г, що обмежує деяку плоску область, або замкнута поверхня Ω, що обмежує область у просторі. Відповідно зміниться і похідна від функції, що фігурує в граничних умовах другого та третього роду. Це буде похідна нормалі n до кривої Г на площині або до поверхні Ω в просторі, причому, як правило, розглядають нормаль, зовнішню по відношенню до області (рис.5).

Наприклад, гранична умова (однорідне) першого роду на площині записується як U| Γ =О, у просторіU| Ω =0. Кордонна умова другого роду на площині має вигляд, а в просторі. Звичайно, фізичний зміст цих умов різний для різних завдань.

При постановці початкових і граничних умов виникає завдання знайти рішення диференціального рівняння, що задовольняє заданим початковим і граничним (крайовим) умовам. Для хвильового рівняння (3) або (4), початкових умов U(x,0)=φ(x), U t (x,0)=ψ(x) та у разі граничних умов першого роду (5), завдання називається першим початково-крайовим завданням для хвильового рівняння. Якщо замість граничних умов першого роду задавати умови другого роду (6) або третього роду (7), то завдання називатиметься відповідно другим і третім початково-крайовим завданням. Якщо граничні умови на різних ділянках кордону мають різні типи, такі початково-крайові завдання називають змішаними.

Розглянемо дві типові електростатичні задачі :

1) Знайти потенціал електричного поля при невідомому місці розташування вихідних зарядів, але заданому електричному потенціалі на межах області. (Наприклад, завдання про розподіл потенціалу електричного поля, створюваного системою нерухомих провідників, поміщених у вакуум і підключених до батарей. Тут можна виміряти потенціал кожного провідника, але встановити розподіл електричних зарядів на провідниках, що залежить від їх форми, дуже складно.)

2) Знайти потенціал електричного поля, створюваного заданим розподілом у просторі електричних зарядів.

Добре відомо, що прямий метод обчислення потенціалу електричного поля у цих завданнях полягає у вирішенні рівняння Лапласа(Завдання 1)

(1)

і рівняння Пуассона(Завдання 2)

. (2)

Рівняння (1), (2) відноситься до класу диференціальних рівнянь у приватних похідних еліптичного типу.

Далі ми розглядатимемо лише окремий випадок еліптичних рівнянь для поля  , що залежить від двох просторових змінних. Цілком очевидно, що для повного вирішення задачі рівняння (1), (2) необхідно доповнити граничними умовами. Розрізняють три типи граничних умов:

1) граничні умови Діріхле(значення  задаються на деякій замкнутій кривій у площині (х,у) і, можливо, на деяких додаткових кривих, розташованих усередині області (рис. 1));

2) граничні умови Неймана(на кордоні визначається нормальна похідна потенціалу );

3) змішане крайове завдання(на кордоні задається лінійна комбінація потенціалу  та його нормальної похідної).

Початкові та граничні умови. Невід'ємним та найважливішим елементом постановки будь-якого завдання механіки суцільних середовищ є формулювання початкових та граничних умов. Їх значення визначається тим, що та чи інша система вирішальних рівнянь визначає цілий клас рухів відповідного деформируемого середовища, і лише завдання відповідних досліджуваному процесу початкових і граничних умов дозволяє виділити з цього класу цікавий окремий випадок, що відповідає вирішуваному практичному завданню.

Початкові умови - це умови, якими задаються значення шуканих характеристичних функцій на момент початку розгляду досліджуваного процесу. Кількість початкових умов, що задаються, визначається кількістю основних невідомих функцій, що входять в систему вирішальних рівнянь, а також порядком входить до цієї системи вищої похідної за часом. Наприклад, адіабатичний рух ідеальної рідини або ідеального газу описується системою шести рівнянь із шістьма основними невідомими - трьома компонентами вектора швидкості, тиском, щільністю та питомою внутрішньою енергією, при цьому порядок похідних цих фізичних величин за часом не перевищує перший порядок. Відповідно до цього як початкові умови мають бути задані початкові поля цих шести фізичних величин: при t =0 ,. У деяких випадках (наприклад, в динамічній теорії пружності) як основні невідомі в системі дозволяють рівняння використовуються не компоненти вектора швидкості, а компоненти вектора переміщення, а рівняння руху містить похідні другого порядку компонент переміщення, що вимагає завдання двох початкових умов для шуканої функції: при t = 0

Більш складним та різноманітним чином при постановці задач механіки суцільних середовищ задаються граничні умови. Граничні умови - це умови, якими задаються значення функцій (або їх похідних по координатах і часу) на поверхні S області, що займається деформованим середовищем. Розрізняють граничні умови кількох типів: кінематичні, динамічні, змішані та температурні.

Кінематичні граничні умови відповідають випадку, коли на поверхні S тіла (або її частини) задаються переміщення або швидкості де координати точок поверхні S, що змінюються в загальному випадку в залежності від часу.

Динамічні граничні умови (або граничні умови у напругах) задаються, коли на поверхні S діють поверхневі сили р. Як випливає з теорії напруг, в цьому випадку на будь-якому елементарному майданчику поверхні з одиничним вектором нормалі п вектор питомих поверхневих сил рп примусово задає вектор повної напруги? напруг (?) у цій точці з поверхневою силою та орієнтацією вектора п відповідної ділянки поверхні: (?) · п = рп або.

Змішані граничні умови відповідають випадку, коли на поверхні S задаються значення кінематичних, динамічних величин або встановлюються взаємозв'язки між ними.

Температурні граничні умови поділяються на кілька груп (пологів). Кордонні умови першого роду задають на поверхні S деформованого середовища певні значення температури Т. Граничні умови другого роду задають на межі вектор теплового потоку q, що з урахуванням закону теплопровідності Фур'є q = -? grad T, по суті, накладає обмеження на характер температурного розподілу на околиці граничної точки. Граничні умови третього роду встановлюють залежність між вектором теплового потоку q, спрямованим до даного середовища з боку навколишнього середовища, і перепадом температур між цими середовищами і т.д.

Слід зазначити, що постановка та вирішення більшості завдань фізики швидкопротікаючих процесів, як правило, здійснюються в адіабатичному наближенні, тому температурні граничні умови використовуються досить рідко, в основному в різних поєднаннях застосовуються кінематичні, динамічні та змішані граничні умови. Розглянемо можливі варіанти завдання граничних умов на окремому прикладі.

На рис. 3 схематично представлений процес взаємодії при проникненні деформованого тіла I деформується перешкоду II. Тіло I обмежено поверхнями S1 та S5, а тіло II – поверхнями S2, S3, S4, S5. Поверхня S5 є межею розділу взаємодіючих деформованих тіл. Вважатимемо, що рух тіла I до початку взаємодії, а також у його процесі відбувається в рідині, що створює певний гідростатичний тиск

Малюнок 3

і задає зовнішні по відношенню до обох тіл поверхневі сили рп = - рп = - рni ri, що діють на будь-який з елементарних майданчиків поверхонь S1 тіла I і S2 перешкоди II, що межують з рідиною. Будемо також вважати, що поверхня S перешкоди жорстко закріплена, а поверхня S4 вільна від дії поверхневих сил (рп = 0).

Для наведеного прикладу різних поверхнях, обмежують деформируемые середовища I і II, повинні задаватися граничні умови всіх трьох основних типів. Очевидно, що на жорстко закріпленій поверхні Sз слід задати кінематичні граничні умови? тел: або Компоненти тензора напруги на поверхні S4 перешкоди також не можуть бути довільними, а взаємопов'язані з орієнтацією її елементарних майданчиків як.

Граничні умови на межі розділу (поверхня S5) взаємодіючих деформованих середовищ є найбільш складними і відносяться до умов змішаного типу, що включають, у свою чергу, кінематичну та динамічну частини (див. рис. 3). Кінематична частина змішаних граничних умов накладає обмеження швидкості руху індивідуальних точок обох середовищ, що знаходяться в контакті в кожній просторовій точці поверхні S5. Можливі два варіанти завдання цих обмежень, проілюстровані на рис. 4, а б. За найпростішим першим варіантом передбачається, що швидкості руху будь-яких двох індивідуальних точок, що знаходяться в контакті, однакові (? = ?) - це так звана умова "прилипання", або умова "зварювання" (див. рис. 4, а). Більш складним і водночас більш адекватним для аналізованого процесу є завдання умови "непроникності", або умови "непротікання" (? · n= ? середовища не можуть проникати

Малюнок 4

один в одного або відставати один від одного, а чи можуть прослизати одна щодо іншої зі швидкістю? - ?, Спрямованої по дотичній до межі розділу ((? I -? II) · n = 0). Динамічна частина змішаних граничних умов межі розділу двох середовищ формулюється з урахуванням третього закону Ньютона з допомогою співвідношень теорії напруг (рис. 4, в). Так, у кожній з двох індивідуальних частинок, що знаходяться в контакті, деформованих середовищ I і II реалізується свій напружений стан, що характеризується тензорами напруг (?)I і (?) II. , Зовнішній по відношенню до даного середовища, діє вектор повної напруги? nI = (?) · nI. У середовищі II тому ж майданчику, але з одиничним вектором нормалі nII , зовнішньої стосовно цього середовища, діє вектор повної напруги?nII =(?)II · пII. З урахуванням взаємності дії та протидії? nI = -? n II , а також очевидної умови nI = --nII = n встановлюється взаємозв'язок між тензорами напруг в обох взаємодіючих середовищах на межі їх розділу: (?)I · п = (?) II ·п або (?ijI - ?ijII) nj = 0. Можливі варіанти завдання граничних умов не вичерпуються розглянутим приватним прикладом. Варіантів завдання початкових і граничних умов так само багато, скільки існує в природі і техніці процесів взаємодії деформованих тіл або середовищ. Вони визначаються особливостями вирішуваного практичного завдання і задаються відповідно до наведених вище загальними принципами.