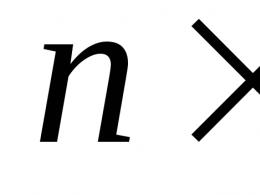Циклічні групи. Циклічні підгрупи Число елементів, що породжують в циклічній групі
Підгрупи циклічних груп
Наступна теорема визначає будову підгруп циклічних груп.
Теорема 1.4. Підгрупа циклічної групи циклічна. Якщо G = (a)uH - непоодинока підгрупа групи G,moH = (ап), де п - найменше натуральне число, таке що а п е Н.
Доказ.Нехай G = (а) та Н- підгрупа групи G.Якщо підгрупа Нодинична, то Н =(е) – циклічна група. Нехай Н- непоодинока підгрупа. Позначимо через пнайменше натуральне число, таке що а п е Н,і доведемо, що Н = (а п).Включення ( а п) з Ночевидно. Доведемо зворотне включення. Нехай h е Н.Оскільки G = (а),то існує цілий показник до,такий що h = а к.Поділимо дона піз залишком: до = nq+ г, де 0 п. Якщо припустити, що г Ф 0, то отримаємо h = а до =а па п ч а г, звідки a r = а~ п чН е Н.Прийшли до суперечності з мінімальністю показника п.Отже, г = 0 і до - nq.Звідси h = a k = а п ч еа"). Таким чином, Нз ( ап), отже, Н = (ад). Теорему доведено.
Породжуючі елементи циклічної групи
Якими елементами може породжуватись циклічна група? Відповідають це питання наступні дві теореми.
Теорема 1.5. Нехай дано циклічну групу G = (а) нескінченного порядку. Тоді (а) - (ак) тоді і тільки тоді, коли до - ± 1.
Доказ.Нехай G = (а),|а| = ° ° і (а) = (Ак).Тоді існує ціла кількість п,таке що а = а кп.Звідси а * "-1 = е,а оскільки | а =то кп - 1 = 0. Але тоді кп = 1 іч-± 1. Зворотне твердження є очевидним.
Теорема 1.6. Нехай дана циклічна група G = (а) порядку т. Тоді (а) = (ак) тоді і тільки тоді, колиНОД(/с, т) = 1.
Доказ.(=>) Нехай (а) = (а до),доведемо, що НОД(/с, т) - 1. Позначимо НОДЦс, т) – d.Оскільки ае (а) - (а до),то а = а кппри деякому цілому п.За якістю порядків елементів звідси випливає, що (1 - кп) : т,тобто. 1 - кп = mtпри деякому цілому t. Але тоді 1 = (кп + mt) : d,звідки d = 1 і НОД(/с, т)= 1.
(Нехай НІД (к, т) = 1. Доведемо, що (а) = (Ак).Увімкнення (а до)з (а) очевидно. Назад, з умови НОД№, т) = 1 слідує існування цілих чисел іі v, таких що кі + mv = 1. Користуючись тим, що | а | - т,отримуємо а = a ku + mv = a ku a mv = а кі е (а до). Отже, (а) = (а до). Теорему доведено.
Нагадаємо, що функція Ейлераф(т) визначається як кількість натуральних чисел, що не перевищують натурального числа ті взаємно простих з т.е.Звідси отримуємо слідство.
Наслідок.Циклічна група (а)порядку тмає ф(т) різних елементів, що породжують.
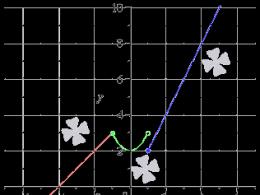
Для надання геометричної наочності теоремі 1.5 зобразимо циклічну групу G = (а)порядку тточками кола А 0, А ь..., А т _ ьділять її на трівних частин. Елемент а доданої групи, що відповідає точці А до,буде породжує тоді і тільки тоді, коли, з'єднуючи послідовно точки А 0 , А до, А 2кі т.д., ми прийдемо до точки А]. Знайдемо всі такі допри т= 10 простим перебором випадків (рис. 1.5). В результаті отримаємо до =1,3, 7, 9. Для циклічної групи (а)це означає, що (а) = (а 3) = (а 7) = (а 9). Назад: знайшовши до,взаємно просте з цим числом т,можна сміливо викреслювати відповідну «зірочку», твердо знаючи, що рано чи пізно потрапиш у кожну точку, бо (а) = ( ак).
Нехай g – довільний елемент групи G. Тоді, приймаючи ми отримаємо мінімальну підгрупу  , породжену одним елементом
, породжену одним елементом  .
.
Визначення.
Мінімальна підгрупа  , породжена одним елементом g групи G, називається циклічною підгрупоюгрупи G.
, породжена одним елементом g групи G, називається циклічною підгрупоюгрупи G.
Визначення.
Якщо група G породжена одним елементом, тобто.  , то вона називається циклічною групою.
, то вона називається циклічною групою.
Нехай  елемент мультиплікативної групи G, тоді мінімальна підгрупа, породжена цим елементом, складається з елементів виду
елемент мультиплікативної групи G, тоді мінімальна підгрупа, породжена цим елементом, складається з елементів виду

Розглянемо ступеня елемента  , тобто. елементи
, тобто. елементи
 .
.
Є дві можливості:
1. Усі ступеня елемента g різні, тобто. 
 , то тут говорять, що елемент g має нескінченний порядок.
, то тут говорять, що елемент g має нескінченний порядок.
2. Є збіги ступенів, тобто. , але  .
.
І тут елемент g має кінцевий порядок.
Справді, нехай, наприклад,  і
і  тоді,
тоді,  , тобто. існують позитивні ступені
, тобто. існують позитивні ступені  елемента
елемента  , рівні одиничному елементу.
, рівні одиничному елементу.
Нехай d – найменший позитивний показник ступеня елемента  , для котрого
, для котрого  . Тоді кажуть, що елемент
. Тоді кажуть, що елемент  має кінцевий порядок, рівний d.
має кінцевий порядок, рівний d.
Висновок.
У будь-якій групі G кінцевого порядку (  ) всі елементи будуть кінцевого порядку.
) всі елементи будуть кінцевого порядку.
Нехай g елемент мультиплікативної групи G, тоді мультиплікативна підгрупа  складається зі всіх різних ступенів елемента g. Отже, кількість елементів у підгрупі
складається зі всіх різних ступенів елемента g. Отже, кількість елементів у підгрупі  збігається з порядком елемента
збігається з порядком елемента  тобто.
тобто.
кількість елементів у групі  одно порядку елемента
одно порядку елемента  ,
,
 .
.
З іншого боку, має місце таке твердження.
Твердження.
Порядок  будь-якого елемента
будь-якого елемента  дорівнює порядку мінімальної підгрупи, породженої цим елементом
дорівнює порядку мінімальної підгрупи, породженої цим елементом  .
.
Доказ.
1.Якщо  - Елемент кінцевого порядку
- Елемент кінцевого порядку  , то
, то
2. Якщо  - Елемент нескінченного порядку, то доводити нічого.
- Елемент нескінченного порядку, то доводити нічого.
Якщо елемент  має порядок
має порядок  , то, за визначенням, всі елементи
, то, за визначенням, всі елементи

різні і будь-який ступінь  збігається з одним із цих елементів.
збігається з одним із цих елементів.
Справді, нехай показник ступеня  , тобто.
, тобто.  - довільне ціле число і нехай
- довільне ціле число і нехай  . Тоді число
. Тоді число  можна уявити у вигляді
можна уявити у вигляді  , де
, де  ,
, . Тоді, використовуючи властивості ступеня елемента g, отримуємо
. Тоді, використовуючи властивості ступеня елемента g, отримуємо
 .
.
Зокрема, якщо .
приклад.
Нехай  - Адитивна абелева група цілих чисел. Група G збігається з мінімальною підгрупою, породженою одним з елементів 1 або –1:
- Адитивна абелева група цілих чисел. Група G збігається з мінімальною підгрупою, породженою одним з елементів 1 або –1:

 ,
,
отже,  - Безкінечна циклічна група.
- Безкінечна циклічна група.
Циклічні групи кінцевого порядку
Як приклад циклічної групи кінцевого порядку розглянемо групу обертань правильного n-кутника щодо його центру  .
.
Елементами групи
є повороти n-кутника проти годинникової стрілки на кути
Елементами групи
 є
є
 ,
,
а з геометричних міркувань ясно, що

 .
.
Група  містить елементів, тобто.
містить елементів, тобто.  , а утворюючим елементом групи
, а утворюючим елементом групи  є
є  , тобто.
, тобто.
 .
.
Нехай  тоді (див. рис. 1)
тоді (див. рис. 1)

Рис. 1 –
Група  – обертання правильного трикутника АВС щодо центру О.
– обертання правильного трикутника АВС щодо центру О.
Алгебраїчна операція у групі  - Послідовне обертання проти годинникової стрілки, на кут, кратний
- Послідовне обертання проти годинникової стрілки, на кут, кратний  , тобто.
, тобто.
Зворотний елемент  – обертання за годинниковою стрілкою на кут 1 , тобто.
– обертання за годинниковою стрілкою на кут 1 , тобто.
 .
.
Таблиця Кечи
Аналіз кінцевих груп найбільш наочно здійснювати з допомогою таблиці Келі, що є узагальненням відомої «таблиці множення».
Нехай група G містить елементи n.
У цьому випадку таблиця Келі є квадратну матрицющо має n рядків та n стовпців.
Кожному рядку та кожному стовпцю відповідає один і лише один елемент групи.
Елемент  таблиці Келі, що стоїть на перетині i-того рядка і j-того стовпця, дорівнює результату виконання операції «множення» i-го елемента з j-тим елементом групи.
таблиці Келі, що стоїть на перетині i-того рядка і j-того стовпця, дорівнює результату виконання операції «множення» i-го елемента з j-тим елементом групи.
Приклад. Нехай група G містить три елементи (g 1, g 2, g 3). Операція в групі «множення». У цьому випадку таблиця Келі має вигляд:

Зауваження. У кожному рядку та кожному стовпці таблиці Келі знаходяться всі елементи групи і лише вони. Таблиця Келі містить повну інформацію про групу. Що можна сказати про властивості цієї групи?
1. Єдиним елементом цієї групи є g1.
2.Група абелева т.к. таблиця симетрична щодо головної діагоналі.
3.Для кожного елемента групи існують зворотні-
для g 1 оберненим є елемент g 1 для g 2 елемент g 3 .
Побудуємо для груп  Келі таблиці.
Келі таблиці.

Для знаходження зворотного елемента елементу, наприклад,  , необхідно в рядку, що відповідає елементу
, необхідно в рядку, що відповідає елементу  знайти стовпець містить елемент
знайти стовпець містить елемент  . Елемент
. Елемент  відповідний даному стовпцю і є зворотним до елемента
відповідний даному стовпцю і є зворотним до елемента  , т.к.
, т.к.  .
.
Якщо таблиця Келі симетрична щодо головної діагоналі, це означає, що

- Тобто. операція у групі коммутативна. Для прикладу, що розглядається, таблиця Келі симетрична щодо головної діагоналі це означає, що операція в  комутативна, тобто.
комутативна, тобто.  ,
,
а група  - Абельова.
- Абельова.
Можна розглядати повну групу перетворень симетрій правильного n – косинця  додавши до операції обертання додаткові операції просторового повороту навколо осей симетрії.
додавши до операції обертання додаткові операції просторового повороту навколо осей симетрії.
Для трикутника  , а група
, а група  містить шість елементів
містить шість елементів
де  це повороти (див. мал. 2) навколо висоти, медіани, бісектриси мають вигляд:
це повороти (див. мал. 2) навколо висоти, медіани, бісектриси мають вигляд:
 ;
;
 ,
,
,
 .
.


Рис. 2.– Група  - Перетворень симетрії правильного трикутника АВС.
- Перетворень симетрії правильного трикутника АВС.
Багато, отримане в результаті цього процесу, позначається в тексті як . Зверніть увагу також, що a 0 = e.
Приклад 5.7
З групи G =< Z 6 , +>можуть бути отримані чотири циклічні підгрупи. Це H 1 =<{0},+>, H 2 =<{0, 2, 4}, +>, H 3 =<{0, 3}, +> і H 4 = G. Зауважимо, що коли операція - додавання, то a n означає множення n на a . Зауважимо також, що у всіх цих групах операція - це додавання за модулем 6 . Нижче показано, як знаходимо елементи цих циклічних підгруп .
a. Циклічна підгрупа , згенерована з 0 - це H 1 має тільки один елемент (нейтральний елемент).
б. Циклічна підгрупа, згенерована на основі 1, - це H4, яка є сама група G.
1 0 mod 6 = 0 1 1 mod 6 = 1 1 2 mod 6 = (1 + 1) mod 6 = 2 1 3 mod 6 = (1 + 1 + 1) mod 6 = 3 1 4 mod 6 = (1 + 1 + 1 + 1) mod 6 = 4 1 5 mod 6 = (1 + 1 + 1 + 1 + 1) mod 6 = 5(зупинка, далі процес повторюється)
в. Циклічна підгрупа , згенерована на основі 2 - це H 2 яка має три елементи: 0, 2 і 4 .
2 0 mod 6 = 0 2 1 mod 6 = 2 2 2 mod 6 = (2 + 2) mod 6 = 4 (зупинка, далі процес повторюється)
г. Циклічна підгрупа , згенерована на основі 3 - це H 3 , яка має два елементи: 0 і 3 .
д. Циклічна підгрупа, згенерована на основі 4 - H 2 ; це - не нова підгрупа.
4 0 mod 6 = 0 4 1 mod 6 = 4 4 2 mod 6 = (4 + 4) mod 6 = 2 (зупинка, далі процес повторюється)
е. Циклічна підгрупа, згенерована на основі 5, - це H 4, вона є сама група G.
5 0 mod 6 = 0 5 1 mod 6 = 5 5 2 mod 6 = 4 5 3 mod 6 = 3 5 4 mod 6 = 2 5 5 mod 6 = 1 (зупинка, далі процес повторюється)
Приклад 5.8
З групи можна отримати три циклічні підгрупи. G має тільки чотири елементи: 1, 3, 7 та 9 . Циклічні підгрупи - ![]()
![]() та . Нижче показано, як знаходимо елементи цих підгруп .
та . Нижче показано, як знаходимо елементи цих підгруп .
a. Циклічна підгрупа, згенерована на основі 1, - це H1. Підгрупа має лише один елемент, а саме – нейтральний.
б. Циклічна підгрупа, згенерована на основі 3, - це H3, яка є групою G.
3 0 mod 10 = 1 3 1 mod 10 = 3 3 2 mod 10 = 9 3 3 mod 10 = 7 (зупинка, далі процес повторюється)
в. Циклічна підгрупа, згенерована на основі 7, - це H3, яка є групою G.
7 0 mod 10 = 1 7 1 mod 10 = 7 7 2 mod 10 = 9 7 3 mod 10 = 3 (зупинка, далі процес повторюється)
г. Циклічна підгрупа, згенерована на основі 9, - це H2. Підгрупа має лише два елементи.
9 0 mod 10 = 1 9 1 mod 10 = 9 (зупинка, далі процес повторюється)
Циклічні групи
Циклічна група- Група, яка є власною циклічною підгрупою. У прикладі 5.7 група має циклічну підгрупу H 5 = G . Це означає, що група G – циклічна група. У цьому випадку елемент, який генерує циклічну підгрупу, може також генерувати групу. Цей елемент далі називається "генератор". Якщо g - генератор, елементи кінцевої циклічної групи можуть бути записані як
(e, g, g 2, ....., g n-1), де g n = e.
Зауважимо, що циклічна група може мати багато генераторів.
Приклад 5.9
а. Група G =
б. Група - циклічна група з двома генераторами, g = 3 та g = 7 .
Теорема Лагранжа
Теорема Лагранжапоказує відношення між порядком групи до порядку підгрупи. Припустимо, що G – група та H – підгрупа G . Якщо порядок G та H - |G| та |H| , відповідно, відповідно до цієї теореми |H| ділить | G | . У прикладі 5.7 | G | = 6 . Порядок підгрупи - | H1 | = 1, | H2 | = 3, | H3 | = 2 та |H4| = 6 . Очевидно, всі ці порядки є дільниками 6 .
Теорема Лагранжа має дуже цікавий додаток. Коли дана група G та її порядок | G | , можуть бути легко визначені порядки потенційних підгруп , якщо можна знайти дільники. Наприклад, порядок групи G =
Порядок елемента
Порядок елементау групі ord (a) (порядок (a)) є найменшим цілим числом n таким, що a n = e . Іншими словами: порядок елемента – порядок групи, яку він генерує.
Приклад 5.10
a. У групі G =
b. У групі G =
- 1. Група Zцілих чисел із операцією складання.
- 2. Група всіх комплексних коренів ступеня nіз одиниці з операцією множення. Оскільки циклічне число ізоморфізм
група є циклічною та елемент утворює.
Ми бачимо, що циклічні групи можуть бути як кінцевими, так і нескінченними.
3. Нехай - довільна група та довільний елемент. Багато є циклічною групою з утворюючим елементом g . Вона називається циклічною підгрупою, породженою елементом g, та її порядок - порядком елемента g. По теоремі Лагранжа порядок елемента є дільником групи. Відображення
що діє за формулою:
Вочевидь є гомоморфізмом та її образ збігається з. Відображення сюр'єктивно тоді і лише тоді, коли група G- циклічна та gїї утворює елемент. У цьому випадку називатимемо стандартним гомоморфізмом для циклічної групи G c обраною твірною g.
Застосовуючи в цьому випадку теорему про гомоморфізм, ми отримуємо важливу властивість циклічних груп: будь-яка циклічна група є гомоморфним чином. Z .
У будь-якій групі Gможуть бути визначені ступеняелемента з цілими показниками:
Має місце властивість
Це очевидно, якщо . Розглянемо випадок, коли . Тоді
Аналогічно розглядаються інші випадки.
З (6) випливає, що
Крім того, за визначенням. Таким чином, ступеня елемента утворюють підгрупу у групі G.Вона називається циклічною підгрупою, породженою елементом,і позначається через .
Можливі два принципово різні випадки: або всі ступені елемента різні, або ні. У першому випадку підгрупа нескінченна. Розглянемо докладніше другий випадок.
Нехай ,; тоді. Найменше із натуральних чисел т,для яких називається в цьому випадку порядкомелемента і позначається через .
Пропозиція 1. Якщо , то
Доказ. 1) Розділимо mна піз залишком:
Тоді через визначення порядку
В силу попереднього
Наслідок. Якщо, підгрупа mo містить n елементів.
Доказ.Справді,
причому всі ці елементи різні.
У тому випадку, коли не існує такого натурального т,що (тобто має місце перший із описаних вище випадків), вважають . Відмітимо, що; порядки всіх інших елементів групи більше 1.
В адитивній групі говорять не про степені елемента , а про його кратних,які позначають через . Відповідно до цього порядок елемента адитивної групи G- це найменше з натуральних чисел т(якщо такі існують), для яких
ПРИКЛАД 1.Характеристика поля є порядок будь-якого ненульового елемента у його адитивній групі.
ПРИКЛАД 2. Вочевидь, що у кінцевої групі порядок будь-якого елемента кінцевий. Покажемо, як обчислюються порядки елементів групи Підстановка називається цикломдовжини і позначається через якщо вона циклічно переставляє
а решта всіх залишає на місці. Очевидно, що порядок циклу довжини дорівнює нар.Цикли і називаються незалежними,якщо серед чисел, що фактично переставляються ними, немає загальних; в цьому випадку . Будь-яка підстановка однозначно розкладається на твір незалежних циклів. Наприклад,
що наочно показано малюнку, де дію підстановки зображено стрілками. Якщо підстановка розкладається на твір незалежних циклів довжин , то
ПРИКЛАД 3.Порядок комплексного числа з групі кінцевий тоді й тільки тоді, коли це число є корінь деякою мірою з одиниці, що, своєю чергою, має місце тоді й лише тоді, коли, a порівняємо з, тобто. .
ПРИКЛАД 4.Знайдемо елементи кінцевого порядку групи рухів площині. Нехай. Для будь-якої точки точки
циклічно переставляються рухом , так що їхній центр тяжіння пронерухомий щодо. Отже, - або поворот на кут виду навколо точки про, або відображення щодо деякої прямої, що проходить через про.
ПРИКЛАД 5. Знайдемо порядок матриці
як елемент групи. Маємо
так що. Звичайно, цей приклад спеціально підібраний: ймовірність того, що порядок удачу обраної матриці буде кінцевий, дорівнює нулю.
Пропозиція 2. Якщо , то
Доказ.Нехай
так що. Маємо
Отже, .
Визначення 1 . Група Gназивається циклічною,якщо існує такий елемент , що . Кожен такий елемент називається породжувальним елементомгрупи G.
ПРИКЛАД 6.Адитивна група цілих чисел є циклічною, оскільки породжується елементом 1.
ПРИКЛАД 7.Адитивна група відрахувань за модулем nє циклічною, оскільки породжується елементом.
ПРИКЛАД 8.Мультиплікативна група комплексного коріння n-го ступеня з 1 є циклічною. Насправді, це коріння суть числа
Ясно що . Отже група породжується елементом.
Легко бачити, що в нескінченній циклічній групі елементами, що породжують, є тільки і. Так, у групі Z породжувальними елементами є лише 1 та - 1.
Число елементів кінцевої групи Gназивається її порядкомта позначається через. Порядок кінцевої циклічної групи дорівнює порядку її елемента, що породжує. Тому із пропозиції 2 випливає
Пропозиція 3 . Елемент циклічної групи порядку n породжує тоді і тільки тоді, коли
ПРИКЛАД 9.Породжуючі елементи групи називаються первісним корінням n-й ступеня з 1. Це коріння виду , де. Наприклад, первісне коріння 12-го ступеня з 1- це.
Циклічні групи - це найпростіші групи, які можна собі уявити. (Особливо вони абелеві.) Наступна теорема дає їх повний опис.
Теорема 1. Будь-яка нескінченна циклічна група ізоморфна групі. Будь-яка кінцева циклічна група порядку п ізоморфна групі.
Доказ. Якщо - нескінченна циклічна група, то через формулу (4) відображення є ізоморфізм.
Нехай - кінцева циклічна група порядку п.Розглянемо відображення
то відображення коректно визначено та бієктивно. Властивість
випливає із тієї ж формули (1). Таким чином, - ізоморфізм.
Теорему доведено.
Для розуміння будови якоїсь групи важливу роль відіграє знання її підгруп. Усі підгрупи циклічної групи можуть бути легко описані.
Теорема 2. 1) Будь-яка підгрупа циклічної групи є циклічною.
2) У циклічній групі порядку n порядок будь-якої підгрупи ділить n і для будь-якого дільника q числа n Існує рівно одна підгрупа порядку q.
Доказ. 1) Нехай - циклічна група і Н- її підгрупа, відмінна від (Одинічна підгрупа, очевидно, є циклічною.) Зауважимо, що якщо для будь-якого, то і . Нехай т- найменше з натуральних чисел, для яких . Доведемо, що . Нехай . Поділимо дона тіз залишком:
звідки з визначення числа тслід, що й, отже, .
2) Якщо , то попереднє міркування, застосоване до (у цьому випадку ), показує, що . При цьому
і Нє єдиною підгрупою порядку qв групі G.Назад, якщо q- будь-який дільник числа пі , то підмножина Н,визначається рівністю (9), є підгрупою порядку q. Теорему доведено.
Слідство . У циклічній групі простого порядку будь-яка непоодинока підгрупа збігається з усією групою.
ПРИКЛАД 10.У групі будь-яка підгрупа має вигляд, де.
ПРИКЛАД 11.У групі коренів n-го ступеня з 1 будь-яка підгрупа є групою коренів q-й ступеня з 1, де.
Розглянемо мультиплікативну групу всіх цілих ступенів двійки (2Z, ), де 2Z = (2n | пе Z). Аналогом цієї групи адитивною мовою є адитивна група парних цілих чисел (2Z, +), 2Z = (2n | п е Z). Дамо загальне визначення груп, окремими прикладами яких є дані групи.
Визначення 1.8. Мультиплікативна група (G,) (Адитивна група (G, +)) називається циклічною,якщо вона складається з усіх цілих ступенів (відповідно, усіх цілих кратних) одного елемента а е G,тобто. G =(А п | п е Z) (відповідно, G - (па | п е Z)). Позначення: (а), читається: циклічна група, породжена елементом а.
Розглянемо приклади.
- 1. Прикладом мультиплікативної нескінченної циклічної групи може бути група всіх цілих ступенів деякого фіксованого цілого числа а Ф±1, вона позначається а р.Таким чином, а г – (а).
- 2. Прикладом мультиплікативної кінцевої циклічної групи є група С„ коренів n-го ступеня з одиниці. Нагадаємо, що коріння n-го ступеня з одиниці знаходиться
за формулою e k= cos---hisin^-, де до = 0, 1, ..., п - 1. Слід- п п
вально, З„ =(е х)= (е х = 1, е х, ef = е 2 ,..., е" -1 = ?„_ х ). Згадаємо, що комплексні числа е до, до = 1, ..., п - 1, зображаються точками одиничного кола, які поділяють її на прівних частин.
- 3. Характерним прикладом адитивної нескінченної циклічної групи є адитивна група цілих чисел Z вона породжується числом 1, тобто. Z = (1). Геометрично вона зображується у вигляді цілих точок числової прямої. Фактично так само зображується мультиплікативна група 2 7 - = (2), у загальному випадку a z = (а),де ціле число а Ф±1 (див. рис. 1.3). Цю подібність зображень ми обговоримо у параграфі 1.6.
- 4. Виберемо у довільній мультиплікативній групі Gдеякий елемент а.Тоді всі цілі ступені цього елемента утворюють циклічну підгрупу (а) = (а п п е Z) G.
- 5. Доведемо, що адитивна група раціональних чисел Q сама не циклічна, а будь-які два її елементи лежать у циклічній підгрупі.
А. Доведемо, що адитивна група Q не циклічна. Припустимо неприємне: нехай Q = (-). Існує ціле число Ь,
не ділить т.е.Оскільки - eQ = (-) = sn-|neZ>, то суще-
Ъ т/ (т J
є ціле число гс 0 , таке що - = п 0 -. Але тоді т = n 0 kb
звідки т:- дійшли суперечності.
Б. Доведемо, що два довільні раціональні числа -
з „ /1
і - належать циклічній підгрупі (-), де тє най- d т/
менше загальне кратне чисел bі d.Справді, нехай т-Ьі
, а аї 1 /1 з cv 1/1
і m = av, u, v е Z, тоді - = - = аї-е(-)і - = - = cv-е (-).
b Ьі т т/ a dv т т/
Теорема 1.3. Порядок циклічної групи дорівнює порядку породжувального елемента цієї групи, тобто.|(а)| = | а |.
Доказ. 1. Нехай | = «>. Доведемо, що всі натуральні ступені елемента арізні. Припустимо неприємне: нехай а к = а ті 0 до Тоді т - до- натуральне число та а т ~ до = е.Але це суперечить тому, що | а = ° °.Таким чином, всі натуральні ступені елемента арізні, звідки випливає нескінченність групи (а). Отже, | (а)| = ° ° = | а |.
2. Нехай | а | = п. Доведемо, що (а) = (е - а 0, а, а 2,..., а" -1 ). З визначення циклічної групи випливає включення (а 0, а, а 2, ..., o" 1-1) з (а). Доведемо зворотне включення. Довільний елемент циклічної групи (а)має вигляд а т,де ті Z. Розділимо шнапс залишком: m-nq + r,де 0 п. Оскільки а п = е,то а т = а п я +г = а п ч? а г = а г е(а 0, а, а 2 ,..., а"- 1 ). -1).
Залишається довести, що всі елементи множини (а 0 , а, а 2 ,..., а "-1) різні. Припустимо неприємне: нехай 0 i п,але а" = а).Тоді він - ета 0 j - i - дійшли суперечності з умовою | а | = п.Теорему доведено.