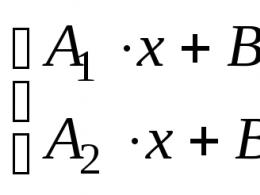Ортогональні системи векторів. Оцінювання просторової орієнтації, або Як не боятися фільтрів Махоні та Маджвіка04.02.2019 Замість укладання: а що ж з фільтром Калмана

44. Система державних органів Франції, виборче право та виборча система Франція є змішаною (напівпрезидентською) республікою, система органів влади якої заснована на принципі поділу влади. Франція сьогодні – це республіка з сильною

Розділ IV. Подвійна система відповідності голові. Система "комахи". Мінісистема

Розділ IV. Подвійна система відповідності голові. Система "комахи". Мінісистема Подвійна система відповідності голові На пальцях кистей і стоп розташовуються дві системи відповідності голові: система "типу людини" та система "типу тварини". Система "типу людини".

Перший емоційний центр – кісткова система, суглоби, кровообіг, імунна система, шкіра.

Перший емоційний центр – кісткова система, суглоби, кровообіг, імунна система, шкіра Здоровий стан органів, пов'язаних з першим емоційним центром, залежить від відчуття безпеки у цьому світі. Якщо ви позбавлені підтримки сім'ї та друзів, яка вам

Якщо на площині вибрати якісь два взаємно перпендикулярні вектори одиничної довжини (рис. 7), то довільний вектор у тій же площині можна розкласти за напрямками цих двох векторів, тобто уявити його у вигляді

де - числа, рівні проекціям вектора на напрями осей Оскільки проекція на вісь дорівнює добутку довжини на косинус кута з віссю, то, згадуючи визначення скалярного добутку, ми можемо написати

Аналогічно, якщо в тривимірному просторі вибрати якісь три взаємно перпендикулярні вектори одиничної довжини, то довільний векторів цьому просторі можна представити у вигляді

У гільбертовому просторі можна розглядати системи попарно ортогональних векторів цього простору, тобто функцій

Такі системи функцій називаються ортогональними системами функцій і грають велику роль аналізі. Вони зустрічаються у найрізноманітніших питаннях математичної фізики, інтегральних рівнянь, наближених обчислень, теорії функцій дійсного змінного і т. п. Упорядкування та об'єднання понять, що належать до таких систем, були одним із стимулів, що призвели на початку XX ст. до створення загального поняття гільбертового простору.

Дамо точні визначення. Система функцій

називається ортогональною, якщо будь-які дві функції цієї системи ортогональні між собою, тобто якщо

У тривимірному просторі ми вимагали, щоб довжини векторів системи дорівнювали одиниці. Згадавши визначення довжини вектора, бачимо, що у разі гільбертового простору ця вимога записується так:

Система функцій, що задовольняє вимогам (13) та (14), називається ортогональною та нормованою.

Наведемо приклади таких систем функцій.

1. На інтервалі розглянемо послідовність функцій

Кожні дві функції цієї послідовності ортогональні між собою. Це перевіряється простим обчисленням відповідних інтегралів. Квадрат довжини вектора в просторі гільберта є інтеграл від квадрата функції. Таким чином, квадрати довжин векторів послідовності

суть інтеграли

тобто e. послідовність наших векторів ортогональна, але не нормована. Довжина першого вектора послідовності дорівнює а все

інші мають довжину. Поділивши кожен вектор на його довжину, ми отримаємо ортогональну та нормовану систему тригонометричних функцій

Ця система є історично одним з перших та найважливіших прикладів ортогональних систем. Вона виникла в роботах Ейлера, Д. Бернуллі, Даламбера у зв'язку із завданням про коливання струни. Її вивчення зіграло істотну роль розвитку всього аналізу.

Поява ортогональної системи тригонометричних функцій у зв'язку із завданням про коливання струни невипадкова. Кожна задача про малі коливання середовища призводить до деякої системи ортогональних функцій, що описують так звані власні коливання даної системи (див. § 4). Наприклад, у зв'язку із завданням про коливання сфери з'являються так звані сферичні функції, у зв'язку із завданням про коливання круглої мембрани або циліндра з'являються так звані циліндричні функції тощо.

2. Можна навести приклад ортогональної системи функцій, кожна функція якої багаточлен. Таким прикладом є послідовність багаточленів Лежандра

тобто є (з точністю до постійного множника) похідна система від . Випишемо перші кілька багаточленів цієї послідовності:

Очевидно, що взагалі є багаточлен ступеня. Ми надаємо читачеві самому переконатися, що ці багаточлени є ортогональною послідовністю на інтервалі

Загальну теорію ортогональних багаточленів (так звані ортогональні багаточлени з вагою) розвинув чудовий російський математик П. Л. Чебишев у другій половині ХІХ ст.

Розкладання по ортогональних системах функцій. Подібно до того, як у тривимірному просторі кожен вектор можна уявити

у вигляді лінійної комбінації трьох попарно-ортогональних векторів одиничної довжини

у функціональному просторі виникає завдання про розкладання довільної функції в ряд за ортогональною та нормованою системою функцій, тобто про представлення функції у вигляді

При цьому збіжність ряду (15) до функції розуміється в сенсі відстані між елементами в просторі гільберта. Це означає, що середнє квадратичне ухилення часткової суми від функції прагне до нуля при , тобто.

Така збіжність називається зазвичай "збіжністю в середньому".

Розкладання по тих чи інших системах ортогональних функцій часто зустрічаються в аналізі та є важливим методом для вирішення задач математичної фізики. Так, наприклад, якщо ортогональна система є системою тригонометричних функцій на інтервалі

то таке розкладання є класичне розкладання функції в тригонометричний ряд

Припустимо, що розкладання (15) можливе для будь-якої функції з простору гільберта, і знайдемо коефіцієнти такого розкладання. Для цього помножимо обидві частини рівності скалярно на ту саму функцію нашої системи. Ми отримаємо рівність

з якого в силу того, що визначається значення коефіцієнта

Ми, як і у звичайному тривимірному просторі (див. початок цього параграфа), коефіцієнти рівні проекціям вектора на напрями векторів .

Згадуючи визначення скалярного твору, отримуємо, що коефіцієнти розкладання функції за ортогональною та нормованою системою функцій

визначаються за формулами

Як приклад розглянемо нормальну ортогональну тригонометричну систему функцій, наведену вище:

Ми отримали формулу для обчислення коефіцієнтів розкладання функції тригонометричний ряд у припущенні, звичайно, що це розкладання можливе.

Ми встановили вид коефіцієнтів розкладання (18) функції за ортогональною системою функцій у припущенні, що таке розкладання має місце. Однак нескінченна ортогональна система функцій може виявитися недостатньою для того, щоб по ній можна було розкласти будь-яку функцію з гільбертового простору. Щоб таке розкладання було можливо, система ортогональних функцій повинна задовольняти додаткову умову - так звану умову повноти.

Ортогональна система функцій називається повною, якщо до неї не можна додати жодної, не рівної тотожно нулю функції, ортогональної до всіх функцій системи.

Легко навести приклад неповної ортогональної системи. Для цього візьмемо якусь ортогональну систему, наприклад ту ж

систему тригонометричних функцій, і виключимо одну з функцій цієї системи, наприклад нескінченна система функцій, що залишилася

буде, як і раніше, ортогональною, звичайно, не буде повною, тому що виключена нами функція: ортогональна до всіх функцій системи.

Якщо система функцій не повна, то не будь-яку функцію з простору гільберта можна по ній розкласти. Дійсно, якщо ми спробуємо розкласти за такою системою нульову функцію ортогональну до всіх функцій системи, то, через формули (18), всі коефіцієнти виявляться рівними нулю, тоді як функція не дорівнює нулю.

Має місце наступна теорема: якщо задана повна ортогональна та нормована система функцій у гільбертовому просторі, то будь-яку функцію можна розкласти в ряд за функціями цієї системи.

При цьому коефіцієнти розкладання дорівнюють проекціям векторів на елементи ортогональної нормованої системи.

Наявна в § 2 теорема Піфагора в гільбертовому просторі дозволяє знайти цікаве співвідношення між коефіцієнтами і функцією Позначимо через різницю між сумою і першими членів її ряду, тобто.

Рівно нулю:

Ортогональна система у разі її повноти може бути використана як базис простору. У цьому розкладання будь-якого елемента можна обчислити за формулами: , де .

Випадок, коли норма всіх елементів називається ортонормованої системою .

Ортогоналізація

Будь-яка повна лінійно незалежна система в кінцевому просторі є базисом. Від простого базису, отже, можна перейти до ортонормованого базису.

Ортогональне розкладання

При розкладанні векторів простору по ортонормированному базису спрощується обчислення скалярного твору: , де і .

Див. також

Wikimedia Foundation. 2010 .

Дивитися що таке "Ортогональна система" в інших словниках:

1) Про … Математична енциклопедія

- (отгреч. orthogonios прямокутний) кінцева або лічильна система фцій, що належать (сепарабельному) гільбертовому простору L2(a,b)(квадратично інтегрованих фцій) і задовольняють умовам Фція g(x)зв. вагою О. с. ф., * означає ... ... Фізична енциклопедія

Система функцій??n(х)?, n=1, 2,..., заданих на відрізку ОРТОГОНАЛЬНЕ ПЕРЕТВОРЕННЯ лінійне перетворення евклідова векторного простору, що зберігає незмінними довжини або (що еквівалентно цьому) скалярні твори векторів … Великий Енциклопедичний словник

Система функцій (φn(х)), n = 1, 2, ..., заданих на відрізку [а, b] та задовольняють наступній умові ортогональності: при k≠l, де ρ(х) деяка функція, яка називається вагою. Наприклад, тригонометрична система 1, sin х, cos х, sin 2х, ... Енциклопедичний словник

Система фцій ((фn(х)), п=1, 2, ..., заданих на відрізку [а, b] і задовольняють слід, умові ортогональності при k не дорівнює l, де р(х) некрая фція , назвою вагою Напр., тригонометрична система 1, sin х, cosх, sin 2х, cos 2x,... О.с.ф. Природознавство. Енциклопедичний словник

Система функцій ((φn (x)), n = 1, 2,..., ортогональних з вагою ρ (х) на відрізку [а, b], тобто таких, що Приклади. Тригонометрична система 1, cos nx , sin nx;n = 1, 2,..., О. с., з вагою 1 на відрізку [π, π]. Велика Радянська Енциклопедія

Ортогональними називаються координати у яких метричний тензор має діагональний вигляд. де d У ортогональних системах координат q = (q1, q², …, qd) координатні поверхні ортогональні одна одній. Зокрема, в декартовій системі координат... Вікіпедія

ортогональна багатоканальна система- - [Л.Г.Суменко. Англо-російський словник з інформаційних технологій. М.: ДП ЦНИИС, 2003.] Тематики інформаційні технології загалом EN ortogonal multiplex …

система координат (фотограмметричного) знімка- Права ортогональна просторова система координат, яка фіксується на фотограмметричному знімку зображеннями координатних позначок. [ГОСТ Р 51833 2001] Тематика фотограмметрія … Довідник технічного перекладача

система- 4.48 система (system): Комбінація взаємодіючих елементів, організованих задля досягнення однієї чи кількох поставлених цілей. Примітка 1 Система може розглядатися як продукт або послуги, що їм надаються. Примітка 2 На практиці… Словник-довідник термінів нормативно-технічної документації

Визначення 1. ) називається ортогональною, якщо всі її елементи попарно ортогональні:

Теорема 1.Ортогональна система нерівних нулю векторів є лінійно незалежною.

(Припустимо, система лінійно залежна: і, для певності, Помножимо скалярну рівність на . Враховуючи ортогональність системи, отримаємо: }

Визначення 2.Система векторів евклідового простору ( ) називається ортонормованою, якщо вона ортогональна і норма кожного елемента дорівнює одиниці.

З теореми 1 відразу слід, що ортонормована система елементів завжди лінійно незалежна. Звідси, у свою чергу, випливає, що в n– мірному евклідовому просторі ортонормована система nвекторів утворює базис (наприклад, ( i, j, k ) у 3 х- мірному просторі). Така система називається ортонормованим базисом,а її вектори – базовими ортами.

Координати вектора в ортонормованому базисі можна легко вирахувати за допомогою скалярного твору: якщо Дійсно, помножуючи рівність на , Отримуємо вказану формулу.

Взагалі всі основні величини: скалярний твір векторів, довжина вектора, косинус кута між векторами і т.д. мають найпростіший вид в ортонормованому базисі. Розглянемо скалярне твір: , оскільки

А всі інші доданки дорівнюють нулю. Звідси одразу отримуємо: ,

* Розглянемо довільний базис. Скалярний твір у цьому базисі дорівнюватиме:

(Тут α iі β j – координати векторів у базисі ( f), а - скалярні твори базисних векторів).

Величини γ ijутворюють матрицю G, звану матрицею Граму.Скалярний твір у матричній формі матиме вигляд: *

Теорема 2.В будь-якому n– мірному евклідовому просторі існує ортонормований базис. Доказ теореми має конструктивний характер і має назву

9. Процес ортогоналізації Граму – Шмідта.

Нехай ( a 1 ,...,a n ) − довільний базис n– мірного евклідового простору (існування такого базису обумовлене n- Мірністю простору). Алгоритм побудови даного базису ортонормованого полягає в наступному:

1.b 1 =a 1 , e 1 = b 1/|b 1|, |e 1|= 1.

2.b 2^e 1 , т.к. (e 1 , a 2)- проекція a 2 на e 1 , b 2 = a 2 -(e 1 , a 2)e 1 , e 2 = b 2/|b 2|, |e 2|= 1.

3.b 3^a 1 , b 3^a 2 , b 3 = a 3 -(e 1 , a 3)e 1 -(e 2 , a 3)e 2 , e 3 = b 3/|b 3|, |e 3|= 1.

.........................................................................................................

k. b k^a 1 ,..., b k^a k-1 , b k = a k - S i=1 k(e i , a k)e i , e k = b k/|b k|, |e k|= 1.

Продовжуючи процес, отримуємо ортонормований базис ( e 1 ,...,e n }.

Примітка 1. За допомогою розглянутого алгоритму можна побудувати ортонормований базис будь-якої лінійної оболонки, наприклад, ортонормований базис лінійної оболонки системи, що має ранг, що дорівнює трьом і складається з п'ятивимірних векторів.

приклад.x =(3,4,0,1,2), y =(3,0,4,1,2), z =(0,4,3,1,2)

Примітка 2.Особливі випадки

Процес Грама - Шмідта також може застосовуватися до нескінченної послідовності лінійно незалежних векторів.

Крім того, процес Грама – Шмідта може застосовуватися до лінійно залежних векторів. В цьому випадку він видає 0 (нульовий вектор) на кроці j , якщо a j є лінійною комбінацією векторів a 1 ,...,a j -1 . Якщо це може статися, то для збереження ортогональності вихідних векторів і запобігання розподілу на нуль при ортонормуванні алгоритм повинен перевірити на нульові вектори і відкидати їх. Кількість векторів, що видаються алгоритмом, дорівнює розмірності підпростору, породженого векторами (тобто кількості лінійно незалежних векторів, які можна виділити серед вихідних векторів).

10. Геометричні векторні простори R1, R2, R3.

Підкреслимо, що безпосередній геометричний сенс мають лише простори

R 1, R 2, R 3 . Простір R n за n > 3 – абстрактний суто математичний об'єкт.

1) Нехай дана система із двох векторів a і b . Якщо система лінійно залежна, то один із векторів, допустимо a , лінійно виражається через інший:

a= k b.

Два вектори, пов'язані такою залежністю, як сказано, називаються колінеарними. Отже, система з двох векторів лінійно залежна тоді і лише

тоді, коли ці вектори колінеарні. Зауважимо, що такий висновок відноситься не тільки до R 3 , але і до будь-якого лінійного простору.

2) Нехай система у R3 складається з трьох векторів a, b, c . Лінійна залежність означає, що один із векторів, скажімо a , Лінійно виражається через інші:

а= k b+ l c . (*)

Визначення. Три вектори a, b, с R 3 , що лежать в одній площині або паралельні одній площині, називаються компланарними

(на мал. зліва вказані вектори a, b, с з однієї площини, а праворуч ті ж вектори відкладені від різних початків і лише паралельні одній площині).

Отже, якщо три вектори R3 лінійно залежні, то вони компланарні. Справедливе та зворотне: якщо вектори a, b, с з R3 компланарні, всі вони лінійно залежні.

Векторним творомвектора a, на вектор b у просторі називається вектор c , що задовольняє наступним вимогам:

Позначення:

Розглянемо впорядковану трійку некомпланарних векторів a, b, c у тривимірному просторі. Сумісний початку цих векторів у точці А(тобто виберемо довільно у просторі точку Аі паралельно перенесемо кожен вектор так, щоб його початок співпав з точкою А). Кінці векторів, поєднаних початками у точці А, Не лежать на одній прямій, так як вектори некомпланарні.

Впорядкована трійка некомпланарних векторів a, b, c у тривимірному просторі називається правою, якщо з кінця вектора c найкоротший поворот від вектора a до вектору b видно спостерігачеві проти годинникової стрілки. І навпаки, якщо найкоротший поворот видно за годинниковою стрілкою, то трійка називається лівий.

Інше визначення пов'язане з правою рукоюлюдини (див. малюнок), звідки і береться назва.

Усі праві між собою (і ліві між собою) трійки векторів називаються однаково орієнтованими.

Про що мова

Поява на Хабре посту про фільтр Маджвіка була символічною подією. Мабуть, загальне захоплення дронами відродило інтерес до завдання оцінювання орієнтації тіла з інерційних вимірів. При цьому традиційні методи, засновані на фільтрі Калмана, перестали задовольняти публіку - чи через високі вимоги до обчислювальних ресурсів, неприйнятних для дронів, чи через складне і неінтуїтивне налаштування параметрів.

Пост супроводжувався дуже компактною і ефективною реалізацією фільтра на C. Однак судячи з коментарів, фізичний зміст цього коду, а також всієї статті, для когось залишився туманним. Що ж, визнаємо чесно: фільтр Маджвіка - найпростіший з групи фільтрів, заснованих на дуже простих і елегантних принципах. Ці принципи я й розгляну у своєму пості. Коду тут не буде. Мій пост - не розповідь про якусь конкретну реалізацію алгоритму оцінювання орієнтації, а швидше запрошення до винаходу власних варіацій на задану тему, яких може бути дуже багато.

Подання орієнтації

Згадаймо основи. Щоб оцінити орієнтацію тіла у просторі, потрібно спочатку вибрати якісь параметри, які разом однозначно визначають цю орієнтацію, тобто. по суті орієнтацію пов'язаної системи координат щодо умовно нерухомої системи – наприклад, географічної системи NED (North, East, Down). Потім необхідно скласти кінематичні рівняння, тобто. виразити швидкість зміни цих параметрів через кутову швидкість гіроскопів. Нарешті, потрібно ввести до уваги векторні виміри від акселерометрів, магнітометрів тощо. Ось найуживаніші способи уявлення орієнтації:

Кути Ейлера- крен (roll,), тангаж (pitch,), курс (heading,). Це найнаочніший і найлаконічніший набір параметрів орієнтації: кількість параметрів точно дорівнює кількості обертальних ступенів свободи. Для цих кутів можна записати кінематичні рівняння Ейлера. Їх дуже люблять у теоретичній механіці, але у завданнях навігації вони малопридатні. По-перше, знання кутів не дозволяє безпосередньо перетворити компоненти будь-якого вектора із пов'язаної в географічну систему координат чи навпаки. По-друге, при тангажі ±90 градусів кінематичні рівняння вироджуються, крен та курс стають невизначеними.

Матриця повороту- матриця розміру 3×3, яку потрібно помножити будь-який вектор у зв'язаної системі координат, щоб отримати той самий вектор в географічній системі: . Матриця завжди ортогональна, тобто. . Кінематичне рівняння для неї має вигляд.
Тут - матриця з компонентів кутової швидкості, виміряних гіроскопами у пов'язаній системі координат:

Матриця повороту трохи менш наочна, ніж кути Ейлера, зате на відміну від них дозволяє безпосередньо перетворювати вектори і при жодному кутовому положенні не позбавляється сенсу. З обчислювальної точки зору її головний недолік - надмірність: заради трьох ступенів свободи вводяться відразу дев'ять параметрів, і їх потрібно оновлювати відповідно до кінематичного рівняння. Завдання можна трохи спростити, скориставшись ортогональністю матриці.

Кватерніон повороту- радикальний, але дуже неінтуїтивний засіб проти надмірності та виродження. Це чотирикомпонентний об'єкт – не число, не вектор і не матриця. На кватерніон можна дивитися із двох ракурсів. По-перше, як формальну суму скаляра і вектора , де - поодинокі вектори осей (що, звісно, ​​звучить абсурдно). По-друге, як на узагальнення комплексних чисел, де тепер використовується не одна, а три різнихуявних одиниць (що звучить не менш абсурдно). Як кватерніон пов'язаний із поворотом? Через теорему Ейлера: тіло завжди можна перевести з однієї заданої орієнтації до іншої одним кінцевим поворотом на деякий кут навколо деякої осі з напрямним вектором . Ці кут і вісь можна поєднати в кватерніон: . Як і матрицю, кватерніон можна використовуватиме безпосереднього перетворення будь-якого вектора з однієї системи координат на іншу: . Як видно, кватерніонне уявлення орієнтації теж страждає на надмірність, але набагато менше, ніж матричне: зайвий параметр всього один. Грунтливий огляд кватерніонів вже був на Хабре. Там йшлося про геометрію та 3D-графіку. Нас цікавить ще й кінематика, оскільки швидкість зміни кватерніону потрібно пов'язати з вимірюваною кутовою швидкістю. Відповідне кінематичне рівняння має вигляд де вектор теж вважається кватерніоном з нульовою скалярною частиною.

Схеми фільтрів

Найбільш наївний підхід до обчислення орієнтації - озброїтися кінематичним рівнянням і оновлювати відповідно до нього будь-який набір параметрів, що сподобався нам. Наприклад, якщо ми вибрали матрицю повороту, то можемо написати цикл із чимось на кшталт C += С * Omega * dt . Результат розчарує. Гіроскопи, особливо MEMS, мають великі і нестабільні зміщення нуля - в результаті навіть у повному спокої орієнтація, що обчислюється, буде мати необмежено накопичується помилку (дрейф). Всі хитрощі, придумані Махоні, Маджвіком та багатьма іншими, не виключаючи і мене, були спрямовані на компенсацію цього дрейфу за рахунок залучення вимірів від акселерометрів, магнітометрів, приймачів GNSS, лагів тощо. Так народилося ціле сімейство фільтрів орієнтації, що спираються на простий базовий принцип.

Основний принцип.Для компенсації дрейфу орієнтації потрібно додати до виміряної гіроскопами кутової швидкості додаткову кутову швидкість, що управляє, побудовану на основі векторних вимірювань інших датчиків. Вектор керуючої кутової швидкості повинен прагнути поєднати напрямки виміряних векторів з їх відомими істинними напрямками.

Тут укладено зовсім інший підхід, ніж у побудові коригувального доданку фільтра Калмана. Головна відмінність саме в тому, що кутова швидкість, що управляє, - не доданок, а множникпри оцінюваній величині (матриці або кватерніоні). Звідси випливають важливі переваги:

• Оцінюючий фільтр можна будувати для самої орієнтації, а не для невеликих відхилень орієнтації від тієї, яку дають гіроскопи. При цьому оцінювані величини автоматично задовольнятимуть усім вимогам, які накладає завдання: матриця буде ортогональною, кватерніон - нормованим.
• Фізичний сенс керуючої кутової швидкості набагато ясніше, ніж коригувального доданку у фільтрі Калмана. Всі маніпуляції робляться з векторами та матрицями у звичайному тривимірному фізичному просторі, а не в абстрактному багатовимірному просторі станів. Це помітно спрощує доопрацювання і налаштування фільтра, а як бонус дозволяє позбутися матриць великої розмірності і великовагових матричних бібліотек.

Тепер подивимося, як ця ідея реалізується у конкретних варіантах фільтрів.

Фільтр Махоні.Вся зубодробна математика оригінальної статті Махоні написана для обґрунтування нескладних рівнянь (32). Перепишемо їх у наших позначеннях. Якщо відволіктися від оцінювання зсувів нуля гіроскопів, то залишаться два ключові рівняння - власне кінематичне рівняння для матриці повороту (з керуючою кутовою швидкістю у вигляді матриці) і закон формування цієї швидкості у вигляді вектора. Припустимо для простоти, що ні прискорень, ні магнітних наведень немає, і завдяки цьому нам доступні вимірювання прискорення вільного падіння від акселерометрів та напруженості магнітного поля Землі від магнітометрів. Обидва вектори вимірюються датчиками у зв'язаній системі координат, а в географічній системі їх положення свідомо відомо: спрямований вгору - на магнітну північ. Тоді рівняння фільтра Махоні виглядатимуть так:

Погляньмо уважно на друге рівняння. Перший доданок у правій частині – це векторний твір. Перший множник у ньому – виміряне прискорення вільного падіння, другий – справжнє. Оскільки множники повинні бути в одній системі координат, то другий множник перетворюється на пов'язану систему множенням на . Кутова швидкість, побудована як векторний добуток, перпендикулярна до площини векторів-множників. Вона дозволяє повертати розрахункове положення пов'язаної системи координат, доки вектори-множники не співпадуть у напрямку - тоді векторний твір обнуляться і поворот припиниться. Коефіцієнт ставить жорсткість такого зворотного зв'язку. Другий доданок виконує аналогічну операцію з магнітним вектором. По суті, фільтр Махоні втілює добре відому тезу: знання двох неколлінеарних векторів у двох різних системах координат дозволяє однозначно відновити взаємну орієнтацію цих систем. Якщо векторів більше двох, це дасть корисну надмірність вимірювань. Якщо вектор лише один, то одну обертальну міру свободи (рух навколо цього вектора) зафіксувати не вдасться. Наприклад, якщо дано тільки вектор, то можна скоригувати дрейф крену та тангажу, але не курсу.

Зрозуміло, у фільтрі Махоні необов'язково скористатися матрицею повороту. Є й неканонічні кватерніонні варіанти.

Віртуальна гіроплатформа.У фільтрі Махоні ми додавали керуючу кутову швидкість до пов'язаної системи координат. Але можна додати її і до розрахункового положення географічної системи координат. Кінематичне рівняння тоді набуде вигляду

Виявляється, такий підхід відкриває шлях до дуже плідних фізичних аналогій. Досить згадати те, з чого починалася гіроскопічна техніка, - курсовертикалі та інерційні навігаційні системи на основі гіростабілізованої платформи у кардановому підвісі.

www.theairlinepilots.com

Завданням платформи була матеріалізація географічної системи координат. Орієнтація носія вимірювалася щодо цієї платформи датчиками кутів на рамах підвісу. Якщо гіроскопи мали дрейф, то за ними дрейфувала і платформа, й у показаннях датчиків кутів накопичувалися помилки. Щоб усунути ці помилки, вводився зворотний зв'язок від акселерометрів, встановлених на платформі. Наприклад, відхилення платформи від обрію навколо північної осі сприймалося акселерометром східної осі. Цей сигнал дозволяв задати кутову швидкість, що управляє , що повертає платформу в горизонт.

Тими самими наочними поняттями ми можемо користуватися і у своїй задачі. Виписане кінематичне рівняння потрібно тоді читати так: швидкість зміни орієнтації є різницею двох обертальних рухів - абсолютного руху носія (перший доданок) і абсолютного руху віртуальної гіроплатформи (другий доданок). Аналогію можна поширити і закон формування керуючої кутової швидкості. Вектор уособлює показання акселерометрів, які нібито стоять на гіроплатформі. Тоді з фізичних міркувань можна написати:

До такого ж результату можна було б дійти і формальним шляхом, зробивши векторне перемноження в дусі фільтра Махоні, але вже не в пов'язаній, а в географічній системі координат. Тільки чи потрібно це?

Перший натяк на корисну аналогію платформної та безплатформної інерційної навігації з'являється, мабуть, у стародавньому патенті «Боїнга». Потім ця ідея активно розроблялася Саличева, а останнім часом - і мною теж. Очевидні переваги такого підходу:

• Керуючу кутову швидкість можна формувати з урахуванням зрозумілих фізичних принципів.
• Природно виявляються розділені горизонтальні та курсовий канали, дуже різні за своїми властивостями та способами корекції. У фільтрі Махоні вони змішані.
• Зручно компенсувати вплив прискорень рахунок залучення даних GNSS, які видаються саме у географічних, а чи не пов'язаних осях.
• Легко узагальнити алгоритм на випадок високоточної інерційної навігації, де доводиться враховувати форму та обертання Землі. Як це зробити у схемі Махоні, я не уявляю.

Фільтр Маджвіка.Маджвік обрав важкий шлях. Якщо Махоні, зважаючи на все, інтуїтивно прийшов до свого рішення, а потім обґрунтував його математично, то Маджвік із самого початку виявив себе формалістом. Він взявся вирішувати завдання оптимізації. Розсудив він так. Задамо орієнтацію кватерніоном повороту. В ідеальному випадку розрахунковий напрямок якогось вимірюваного вектора (нехай у нас це буде) збігається з істинним. Тоді буде. Насправді це не завжди можна досягти (особливо якщо векторів більше ніж два), але можна спробувати мінімізувати відхилення від точної рівності. Для цього введемо критерій мінімізації

Мінімізація вимагає градієнтного спуску - руху дрібними кроками убік, протилежну градієнту, тобто. протилежну якнайшвидшому зростанню функції. До речі, Маджвік припускається помилки: у всіх своїх роботах він взагалі не вводить і наполегливо пише замість , хоча фактично обчислює саме .

Градієнтний спуск у результаті призводить до наступної умови: для компенсації дрейфу орієнтації потрібно додати до швидкості зміни кватерніону з кінематичного рівняння новий негативний доданок, пропорційний :

Тут Маджвік трохи відступає від нашого «базового принципу»: він додає коригуючий член не до кутової швидкості, а до швидкості зміни кватерніону, а це не зовсім те саме. Через війну може бути, що оновлений кватерніон перестане бути одиничним і, відповідно, втратить здатність представляти орієнтацію. Тому для фільтра Маджвіка штучне нормування кватерніону – життєво важлива операція, у той час як для інших фільтрів – бажане, не необов'язкове.

Вплив прискорень

До цього часу передбачалося, що справжніх прискорень немає і акселерометри вимірюють лише прискорення вільного падіння. Це дозволяло отримати стандарт вертикалі і з його допомогою компенсувати дрейф крену і тангажу. Проте у випадку акселерометри, незалежно від свого принципу дії, вимірюють здавалося прискорення- Векторну різницю істинного прискорення і прискорення вільного падіння. Напрямок прискорення, що здається, не збігається з вертикаллю, і в оцінках крену і тангажу з'являються помилки, викликані прискореннями.

Це легко проілюструвати за допомогою аналогії віртуальної гіроплатформи. Її система корекції влаштована те що платформа зупиняється у тому кутовому положенні, у якому обнулюються сигнали акселерометрів, нібито встановлених у ньому, тобто. коли вимірюваний вектор стає перпендикулярним осям чутливості акселерометрів. Якщо прискорень немає, це збігається з горизонтом. Коли виникають горизонтальні прискорення, гіроплатформ відхиляється. Можна сказати, що гіроплатформа схожа на сильно задемпфований маятник або виска.

У коментарях до посту про фільтр Маджвіка промайнуло питання про те, чи можна сподіватися, що цей фільтр менш сприйнятливий до прискорень, ніж, наприклад, фільтр Махоні. На жаль, всі описані тут фільтри експлуатують одні й ті ж фізичні принципи і тому страждають від тих самих проблем. Обдурити фізику математикою не можна. Що ж тоді робити?

Найпростіший і грубіший спосіб придумали ще в середині минулого століття для авіаційних гіровертикалей: зменшувати або зовсім обнуляти кутову швидкість, що управляє, за наявності прискорень або кутової швидкості курсу (яка свідчить про вход у віраж). Той самий метод можна перенести і в нинішні безплатформні системи. Про прискорення при цьому потрібно судити за значеннями , а не , які у віражі власними силами нульові. Однак у величині який завжди можна відрізнити справжні прискорення від проекцій прискорення вільного падіння, зумовлених цим нахилом гіроплатформи, який потрібно усунути. Тому метод працює ненадійно – зате не вимагає жодних додаткових датчиків.

Більш точний спосіб ґрунтується на використанні зовнішніх вимірювань швидкості від приймача GNSS. Якщо відома швидкість, то її можна чисельно продиференціювати та отримати справжнє прискорення. Тоді різниця буде точно дорівнює незалежно від руху носія. Їй можна скористатися як зразком вертикалі. Наприклад, можна задати управляючі кутові швидкості гіроплатформи у вигляді

Зміщення нуля датчиків

Сумною особливістю гіроскопів та акселерометрів споживчого класу є великі нестабільності зсувів нуля за часом та за температурою. Для їх усунення недостатньо одного тільки заводського або лабораторного калібрування - потрібне дооцінювання під час роботи.

Гіроскопи.Розберемося зі зсувами нуля гіроскопів. Розрахункове становище пов'язаної системи координат уникає свого істинного становища з кутовою швидкістю, яка визначається двома протидіючими факторами - зміщеннями нуля гіроскопів та керуючої кутової швидкістю: . Якщо системі корекції (наприклад, у фільтрі Махоні) вдалося зупинити догляд, то в режимі, що встановився, виявиться . Іншими словами, у керуючій кутовій швидкості міститься інформація про невідоме обурення, що діє. Тому можна застосувати компенсаційне оцінювання: ми не знаємо величини обурення безпосередньо, проте знаємо, який коригуючий вплив потрібно, щоб його врівноважити. На цьому ґрунтується оцінювання зсувів нуля гіроскопів. Наприклад, у Махоні оцінка оновлюється за законом

Однак результат у нього виходить дивний: оцінки досягають 0,04 рад/с. Такої нестабільності зміщень нуля не буває навіть у найгірших гіроскопів. Підозрюю, проблема пов'язана з тим, що Махоні не використовує GNSS або інші зовнішні датчики – і повною мірою страждає від впливу прискорень. Тільки по вертикальній осі, де прискорення не шкодять, оцінка виглядає більш менш здоровою:

Mahony et al., 2008

Акселерометри.Оцінити зміщення нуля акселерометрів набагато складніше. Інформацію про них доводиться витягувати з тієї ж кутової швидкості, що управляє. Однак у прямолінійному русі ефект зсувів нуля акселерометрів не відрізняється від нахилу носія або перекосу установки блоку датчиків на ньому. Жодної добавки до акселерометрів не створюють. Добавка з'являється тільки при розвороті, що дозволяє розділити і незалежно оцінити похибки гіроскопів і акселерометрів. Приклад того, як це можна зробити, є у моїй статті. Ось малюнки звідти:

Замість укладання: а що ж з фільтром Калмана?

У мене немає сумніву, що описані тут фільтри майже завжди матимуть перевагу перед традиційним фільтром Калмана щодо швидкодії, компактності коду та зручності налаштування – для цього вони й створювалися. Щодо точності оцінювання, то тут все не так однозначно. Мені зустрічалися невдало спроектовані фільтри Калмана, які й точно помітно програвали фільтру з віртуальною гіроплатформою. Маджвік також доводив вигоди свого фільтра щодо якихоськалманівських оцінок. Однак для одного і того ж завдання оцінювання орієнтації можна спорудити не менше десятка різних схем фільтра Калмана, і у кожної буде незліченна кількість варіантів налаштування. У мене немає жодних приводів думати, що фільтр Махоні або Маджвіка виявиться точнішим. найкращого з можливихфільтрів Калмана. І звичайно, за калманівським підходом завжди залишиться перевага універсальності: він не накладає жодних жорстких обмежень на конкретні динамічні властивості системи, що оцінюється.