ДЕЛЬТА-ФУНКЦІЯ

Визначення. Дельта-функція

(2.1)

а узагальненою функцією

Рис.1. Дельта-функція

Умова нормування

, . (2.2)

a, як показано на рис 1, б

парність функціївипливає з (2.1)

. (2.2а)

, (2.2б)

як випливає з рис 1, б.

Ортонормованість. Безліч функцій

Властивості ДЕЛЬТА-ФУНКЦІЇ

Фільтруюча властивість

отримуємо

б, знаходимо

,

, . (2.5)

Ортонормованість базису

В (2.5) вважаємо

, ,

. (2.7)

Виконується

,

, (2.8)

Доказ

Спрощення аргументу

Якщо – коріння функції тоді

. (2.9)

Доказ

.

У малому околиці розкладаємо у ряд Тейлора

і обмежуємося першими двома доданками

Використовуємо (2.8)

Порівнюємо підінтегральні функції та отримуємо (2.9).

Згортка

З визначення згортки (1.22)

,

при отримуємо

.

Вважаємо , і знаходимо

та (2.35а) дають

. (2.35б)

отримуємо

. (2.36а)

та (2.36а) дають

. (2.36б)

. (2.37а)

отримуємо

. (2.37б)

Гребінчаста функція

(2.53)

Моделює необмежену кристалічну решітку, антену та інші періодичні структури.

При Фур'є-перетворенні гребінчаста функція перетворюється на гребінчасту функцію.

,

(2.8)

отримуємо

. (2.54)

Властивості

Функція парна

,

періодична

,

період. Фільтруюча властивість дельта-функцій дає

. (2.55)

Фур'є-образ

Для періодичної функції із періодом LФур'є-образ виражається через коефіцієнти Фур'є

, (1.47)

, (1.49)

Для гребінчастої функції з періодом отримуємо

,

де враховано фільтруючу властивість дельта-функції. З (1.47) знаходимо Фур'є-образ

. (2.56)

Фур'є-образом гребінчастої функції є гребінчаста функція.

З (2.56) за теоремою Фур'є про масштабне перетворення аргументу отримуємо

. (2.59)

Збільшення періоду гребінчастої функції ()зменшує період та збільшує амплітуду її спектру .

Ряд Фур'є

Використовуємо

Для , отримуємо

ДЕЛЬТА-ФУНКЦІЯ

Визначення. Дельта-функція

моделює точкове обурення та визначається у вигляді

(2.1)

Функція дорівнює нулю у всіх точках, крім де її аргумент дорівнює нулю, і де функція нескінченна, як показано на рис. 1, а. Завдання значеннями в точках аргументу неоднозначно через її звернення до нескінченності, тому дельта-функція є узагальненою функцією і вимагає довизначення у вигляді нормування.

Рис.1. Дельта-функція

Умова нормування

, . (2.2)

Площа під графіком функції дорівнює одиниці в будь-якому інтервалі, що містить точку a, як показано на рис 1, б. Тому дельта-функція моделює точкове обурення одиничної величини.

парність функціївипливає з (2.1)

. (2.2а)

З симетрії щодо точки отримуємо

, (2.2б)

як випливає з рис 1, б.

Ортонормованість. Безліч функцій

утворює ортонормований нескінченномірний базис.

Дельта-функцію застосував в оптиці Кірхгоф у 1882 р., в електромагнітній теорії – Хевісайд у 90-х роках ХІХ ст.

Густав Кірхгоф (1824–1887) Олівер Хевісайд (1850–1925)

Олівер Хевісайд – вчений самоучка, вперше використав у фізиці вектори, розробив векторний аналіз, ввів поняття оператора та розробив операційне обчислення – операторний метод розв'язання диференціальних рівнянь. Ввів функцію включення, названу пізніше його ім'ям, використав точкову імпульсну функцію – дельта-функцію. Застосував комплексні числа теорії електричних ланцюгів. Вперше записав рівняння Максвелла у вигляді 4-х рівностей замість 20 рівнянь, як було у Максвелла. Ввів терміни: провідність, імпеданс, індуктивність, електрет . Розробив теорію телеграфного зв'язку великі відстані, передбачив наявність в Землі іоносфери – шар Кеннелли–Хевисайда.

Математичну теорію узагальнених функцій розробив Сергій Львович Соболєв у 1936 р. Він був одним із засновників Новосибірського Академмістечка. Його ім'ям названо Інститут математики СО РАН.

Сергій Львович Соболєв (1908-1989)

Властивості ДЕЛЬТА-ФУНКЦІЇ

Фільтруюча властивість

Для гладкої функції , що не має розривів, (2.1)

отримуємо

Вважаючи , і використовуючи дельта-функцію як межі при , показаного на рис. 1, б, знаходимо

,

Інтегрування дає фільтруючу властивість в інтегральній формі

, . (2.5)

Ортонормованість базису

В (2.5) вважаємо

, ,

і отримуємо умову ортонормованості базису з безперервним спектром

. (2.7)

Масштабне перетворення аргументу

Виконується

,

, (2.8)

Доказ

Інтегруємо добуток дельта функції з гладкою функцією по інтервалу, де:

де зроблено заміну змінної та використано фільтруючу властивість. Порівняння початкового та кінцевого виразів дає (2.8).

Спрощення аргументу

Якщо – коріння функції тоді

. (2.9)

Доказ

Функція відмінна від нуля лише поблизу точок, у цих точках вона нескінченна.

Для знаходження ваги, з якою входить нескінченність, інтегруємо твір з гладкою функцією інтервалу . Не рівні нулю вклади лише в околицях точок

. , (2.10) .. (2.35а)

Теорема Фур'є про усунення аргументу

та (2.35а) дають

. (2.35б)

З (1.1) та інтегрального уявлення (2.24)

отримуємо

. (2.36а)

Теорема Фур'є про фазове зрушення функції

та (2.36а) дають

. (2.36б)

З (2.35а) та теореми Фур'є про диференціювання

. (2.37а)

З (2.36а) та теореми Фур'є про множення на аргумент

отримуємо

. (2.37б)

Визначення. Дельта-функція

,

моделює точкове обурення та визначається у вигляді

(2.1)

Функція дорівнює нулю у всіх точках, крім
, Де її аргумент дорівнює нулю, і де функція нескінченна, як показано на рис. 1, а. Завдання
значеннями в точках аргументу неоднозначно через її звернення до нескінченності, тому дельта-функція є узагальненою функцією і вимагає довизначення у вигляді нормування.

Рис.1. Дельта-функція

Умова нормування

,
. (2.2)

Площа під графіком функції дорівнює одиниці в будь-якому інтервалі, що містить точку a, як показано на рис 1, б. Тому дельта-функція моделює точкове обурення одиничної величини.

парність функціївипливає з (2.1)

,

. (2.2а)

З симетрії
щодо точки
отримуємо

, (2.2б)

як випливає з рис 1, б.

Ортонормованість. Безліч функцій

,
,

утворює ортонормований нескінченномірний базис.

Дельта-функцію застосував в оптиці Кірхгоф у 1882 р., в електромагнітній теорії – Хевісайд у 90-х роках ХІХ ст.

Густав Кірхгоф (1824–1887) Олівер Хевісайд (1850–1925)

Олівер Хевісайд – вчений самоучка, вперше використав у фізиці вектори, розробив векторний аналіз, ввів поняття оператора та розробив операційне обчислення – операторний метод розв'язання диференціальних рівнянь. Ввів функцію включення, названу пізніше його ім'ям, використав точкову імпульсну функцію – дельта-функцію. Застосував комплексні числа теорії електричних ланцюгів. Вперше записав рівняння Максвелла у вигляді 4-х рівностей замість 20 рівнянь, як було у Максвелла. Ввів терміни: провідність, імпеданс, індуктивність, електрет . Розробив теорію телеграфного зв'язку на великі відстані, передбачив наявність Землі іоносфери – шар Кеннеллі-Хевісайда .

Математичну теорію узагальнених функцій розробив Сергій Львович Соболєв у 1936 р. Він був одним із засновників Новосибірського Академмістечка. Його ім'ям названо Інститут математики СО РАН, засновником та директором якого він був з 1957 по 1983 рік.

Сергій Львович Соболєв (1908-1989)

Властивості дельта-функції Фільтруюча властивість

Для гладкої функції
, що не має розривів, (2.1)

отримуємо фільтруюча властивість дельта-функції у диференціальній формі , що стосується однієї точки
:

Вважаємо
, і використовуємо для дельта-функції межу при
, показаний на мал. 1, б. Знаходимо

,

. (2.4)

Інтегруємо (2.3) за інтервалом
, Що включає точку a, враховуємо нормування (2.2) та отримуємо фільтруюча властивість дельта-функції в інтегральній формі

,
. (2.5)

Ортонормованість базису

В (2.5) вважаємо

,
,

і отримуємо умову ортонормованості базису
з безперервним спектром значень

. (2.7)

1. Одинична функція включення Хевісайда, дельта функція Дірака та їх основні властивості

Поодинока функція Хевісайду

Функція Хевісайду (одинична ступінчаста функція, функція одиничного стрибка, включена одиниця) - кусково-постійна функція, що дорівнює нулю для негативних значень аргументу та одиниці – для позитивних. У нулі ця функція не визначена, проте її зазвичай довизначають у цій точці деяким числом, щоб область визначення функції містила всі точки дійсної осі. Найчастіше неважливо, яке значення функція набуває в нулі, тому можуть використовуватися різні визначення функції Хевісайда, зручні з тих чи інших міркувань, наприклад:

Інше поширене визначення:

Функція Хевісайда широко використовується в математичному апараті теорії управління та теорії обробки сигналів для представлення сигналів, що переходять у певний момент часу з одного стану до іншого. У математичній статистиці ця функція застосовується для запису емпіричної функції розподілу.

Функція Хевісайда є первісною функцією для дельта-функції Дірака, H" = δ, це також можна записати як:

Дельта-функція

δ -функція(абодельта-функція,δ -функція Дірака, діраковська дельта, одинична імпульсна функція) дозволяє записати просторову щільність фізичної величини (маса, заряд, інтенсивність джерела тепла, сила тощо), зосередженої або доданої в одній точці.

Наприклад, щільність одиничної точкової маси, що знаходиться в точці aевклідова простору записується за допомогою δ-функції у вигляді δ( x − a). Також застосовна для опису розподілу заряду, маси тощо на поверхнях або лініях.

δ-функція є узагальнена функція, це означає, що формально вона визначається як безперервний лінійний функціонал на просторі функцій, що диференціюються.

δ-функція не є функцією в класичному сенсі, проте неважко вказати послідовності звичайних класичних функцій, що слабо сходяться до δ-функції.

Можна розрізняти одномірну та багатовимірну дельту-функцію, проте останні можуть бути представлені у вигляді добутку одномірних у кількості, що дорівнює розмірності простору, на якому визначена багатовимірна.

Властивості

Первоподібною одномірною дельта-функцією є функція Хевісайду:

Фільтруюча властивість дельта-функції:

2. Фільтрверхніх частот(ФВЧ)- електронний або будь-який інший фільтр, що пропускає високі частоти вхідного сигналу, при цьому пригнічуючи частоти менше, ніж частота зрізу. Ступінь придушення залежить від типу фільтра. Пасивний фільтр - електронний фільтр, що складається лише з пасивних компонентів, таких як, наприклад, конденсатори та резистори. Пасивні фільтри не вимагають джерела енергії для свого функціонування. На відміну від активних фільтрів пасивних фільтрах немає посилення сигналу по потужності. Майже завжди пасивні фільтри є лінійними.

найпростіший електронний фільтр верхніх частот складається з послідовно з'єднаних конденсаторів та резистора. Конденсатор пропускає лише змінний струм, а вихідна напруга знімається із резистора. Твір опору на ємність (R×C) є постійної часу для такого фільтра, яка обернено пропорційна частоті зрізу в герцах.

(Або так)

Перетворити характеристику ФНЧ на характеристику ФВЧможна за допомогою заміни змінної: де n - гранична частота смуги пропускання ФНЧ та

Перетворення схем пасивнихLC-фільтрів. Заміна змінних (2.31) і (2.32) у виразі для квадрата АЧХ | H p (j) | 2 фільтри нижніх частот призводить при реалізації цієї функції до перетворення схеми ФНЧ на схеми ФВЧ та ПФ. Індуктивний опір ФНЧ j н.ч L н.ч переходить при перетворенні частот (17.31) в опір: тобто в ємнісний опір ФВЧ, де C в.ч = 1/п 2 L н.ч.

Ємнісна провідність: перетворюється на індуктивну провідність фільтра ВЧ з індуктивністю L в.ч = 1/ п 2 C н.ч.

Перетворення передавальних функцій активних RC-фільтрів. В активних RC-фільтрах для того, щоб перейти від передавальної функції ФНЧ-прототипу до передавальних функцій ФВЧ та ПФ, слід здійснити заміну комплексної змінної р. З (17.31) отримуємо для ФВЧ

або (17.34) де н.ч = н.ч/п та в.ч = в.ч/п.

(Або як писали на факультативі)

Вступ

Розвиток науки потребує її теоретичного обгрунтування дедалі більше «високої математики», однією з досягнень якої є узагальнені функції, зокрема функція Дірака. В даний час теорія узагальнених функцій актуальна у фізиці та математиці, так як має ряд чудових властивостей, що розширюють можливості класичного математичного аналізу, розширює коло завдань, що розглядаються, і до того ж призводить до значних спрощень у обчисленнях, автоматизуючи елементарні операції.

Цілі даної роботи:

1) вивчити поняття функції Дірака;

2) розглянути фізичний та математичний підходи до її визначення;

3) показати застосування до знаходження похідних розривних функцій.

Завдання роботи: показати можливості використання дельта-функції у математиці та фізиці.

У роботі представлені різні способи визначення та введення дельта-функції Дірака, її застосування під час вирішення завдань.

Визначення функції Дірака

У різних питаннях математичного аналізу термін «функція» доводиться розуміти з різним ступенем спільності. Іноді розглядаються безперервні, але не диференційовані функції, в інших питаннях доводиться припускати, що йдеться про функції, що диференціюються один або кілька разів і т.д. Однак у ряді випадків класичне поняття функції, навіть трактується у найширшому сенсі, тобто. як довільне правило, що відноситься до кожного значення x з області визначення цієї функції деяке число y = f (x), виявляється недостатнім.

Ось важливий приклад: застосовуючи апарат математичного аналізу до тих чи інших завдань, нам доводиться стикатися з таким становищем, коли ті чи інші операції аналізу виявляються нездійсненними; наприклад, функцію, що не має похідної (у деяких точках або навіть усюди), не можна диференціювати, якщо похідну розуміти як елементарну функцію. Труднощів такого типу можна було б уникнути, обмежившись розглядом одних лише аналітичних функцій. Проте таке звуження запасу допустимих функцій у часто дуже небажано. Необхідність подальшого розширення поняття функції стала особливо гострою.

У 1930 році для вирішення завдань теоретичної фізики найбільшому англійському фізику-теоретику П. Діраку, одному із засновників квантової механіки, не вистачило апарату класичної математики, і він увів новий об'єкт, названий "дельта-функцією", який виходив далеко за рамки класичного визначення функції .

П. Дірак у книзі «Принципи квантової механіки» визначив дельта-функцію д(x) наступним чином:

Крім того, задається умова:

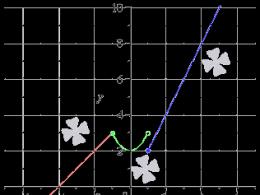
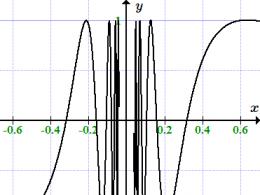
Наочно можна уявити графік функції, схожої на д(x), як показано на малюнку 1. Чим більш вузькою зробити смужку між лівою та правою гілкою, тим вище має бути ця смужка, щоб площа смужки (тобто інтеграл) зберігала своє задане значення, що дорівнює 1. При звуженні смужки ми наближаємося до виконання умови д(x) = 0при x? 0функція наближається до дельта-функції.

Таке уявлення загальноприйняте у фізиці.

Слід наголосити, що д(x)не є функцією в звичайному сенсі, тому що з цього визначення випливають несумісні умови з погляду класичного визначення функції та інтеграла:

при і.

У класичному аналізі немає функції, що володіє властивостями, запропонованими Діраком. Лише через кілька років у роботах С.Л. Соболєва та Л. Шварца дельта-функція отримала своє математичне оформлення, але не як звичайна, а як узагальнена функція.

Перш ніж переходити до розгляду функції Дірака, введемо основні визначення та теореми, які нам будуть необхідні:

Визначення 1. Зображенням функції f(t) або L - зображенням заданої функції f(t) називають функцію комплексної змінної p, що визначається рівністю:

Визначення 2.Функція f(t), визначена так:

називається одиничною функцією Хевісайдута позначається через. Графік цієї функції зображено на рис.2

Знайдемо L- зображення функції Хевісайду:

Нехай функція f(t) при t<0 тождественно равна нулю (рис.3). Тогда функция f(t-t 0) будет тождественно равна нулю при t

Для знаходження зображення д(x) за допомогою допоміжної функції розглянемо теорему запізнення:

Теорема 1. Якщо F(p) є зображенням функції f(t), тобто зображенням функції f(t-t 0 ), тобто якщо L(f(t))=F(p), то .

Доказ.

За визначенням зображення маємо

Перший інтеграл дорівнює нулю, оскільки f(t-t 0 )=0 при t 0 . В останньому інтегралі зробимо заміну змінної t-t 0 =z:

Таким чином, .

Для одиничної функції Хевісайда було встановлено, що. З доведеної теореми слід, що з функції, L -зображенням буде, тобто

Визначення 3.Безперервна або шматково-безперервна функція д(t,л)аргументу t, що залежить від параметра л, називається голкоподібною, якщо:

Визначення 4.Числову функцію f, визначену на деякому лінійному просторі L, називають функціоналом.

Задамо сукупність тих функцій, у яких діятимуть функціонали. Як цю сукупність розглянемо безліч Kвсіх речових функцій ц(x), кожна з яких має безперервні похідні всіх порядків і фінітна, тобто звертається в нуль поза деякою обмеженою областю (своєю для кожної з функцій ц(x)). Ці функції називатимемо основними, а всю їхню сукупність До - основним простором.

Визначення 5. Узагальненою функцієюназивається всякий лінійний безперервний функціонал, визначений на основному просторі До.

Розшифруємо визначення узагальненої функції:

1) узагальнена функція fє функціонал на основних функціях ц, тобто кожної цзіставляється (комплексне) число (f, ц);

2) функціонал fлінійний, тобто для будь-яких комплексних чисел л 1 і л 2 та будь-яких основних функцій ц 1 і ц 2 ;

3) функціонал fбезперервний, тобто якщо.

Визначення 6.Імпульс- одиночний, короткочасний стрибок електричного струму чи напруги.

Визначення 7.Середня щільність- Відношення маси тіла mдо його обсягу V, тобто .

Теорема 2.(Узагальнена теорема про середнє).

Якщо f(t) - безперервна, а - інтегрована функції на , причому на цьому відрізку не змінює знаку, то де.

Теорема 3.Нехай функція f(x), обмежена і має трохи більше кінцевого числа точок розриву. Тоді функція є первісною для функції f(x) на відрізку і для будь-якої первісної Ф(x) справедлива формула.

Визначення 8.Сукупність усіх безперервних лінійних функціоналів, визначених на певному лінійному просторі Е, утворює лінійний простір. Воно називається простором, пов'язанимз Е, і позначається Е * .

Визначення 9.Лінійний простір Е, у якому задана деяка норма, називається нормованим простором.

Визначення 10.Послідовність називається слабо сходитьсядо, якщо для кожного виконано співвідношення.

Теорема 4.Якщо (x n ) - слабко сходящаяся послідовність у нормованому просторі, то існує таке постійне число С, що .