Якщо попередньо побудувати асимптоти кривої, то у багатьох випадках побудова графіка функції полегшується.

Доля асимптоти сповнена трагізму. Уявіть собі, як це: все життя рухатися прямою до заповітної мети, підійти до неї максимально близько, але так і не досягти її. Наприклад, прагнути поєднати свій життєвий шлях із шляхом бажаної людини, в якийсь момент наблизитися до неї майже впритул, але навіть не торкнутися її. Або прагнути заробити мільярд, але до досягнення цієї мети та запису в книгу рекордів Гіннеса для свого випадку не дістає сотих часток цента. І тому подібне. Так і з асимптотою: вона постійно прагне досягти кривої графіка функції, наближається до нього на мінімальну можливу відстань, але не стосується його.

Визначення 1. Асимптотами називаються такі прямі , яких скільки завгодно близько наближається графік функції, коли змінна прагне плюс нескінченності чи мінус нескінченності.

Визначення 2. Пряма називається асимптотою графіка функції, якщо відстань від змінної точки Мграфіка функції до цієї прямої прагне нулю при необмеженому видаленні точки Мвід початку координат по будь-якій галузі графіка функції.

Розрізняють три види асимптот: вертикальні, горизонтальні та похилі.

Вертикальні асимптоти

Перше, що потрібно дізнатися про вертикальні асимптоти: вони паралельні осі Ой .

Визначення. Пряма x = aє вертикальною асимптотою графіка функції якщо точка x = aє точкою розриву другого родудля цієї функції.

З визначення слідує, що пряма x = aє вертикальною асимптотою графіка функції f(x) , якщо виконується хоча б одна з умов:

При цьому функція f(x) може бути взагалі не визначена відповідно при x ≥ aі x ≤ a .

Зауваження:

приклад 1.Графік функції y=ln xмає вертикальну асимптоту x= 0 (тобто збігається з віссю Ой) на межі області визначення, так як межа функції при прагненні іксу до нуля справа дорівнює мінус нескінченності:

(Мал. зверху).

самостійно, а потім переглянути рішення

приклад 2.Знайти асимптоти графіка функції.

Приклад 3.Знайти асимптоти графіка функції

Горизонтальні асимптоти

Перше, що потрібно дізнатися про горизонтальні асимптоти: вони паралельні осі Ox .

Якщо (межа функції при прагненні аргументу до плюс або мінус нескінченності дорівнює деякому значенню b), то y = b – горизонтальна асимптота кривий y = f(x ) (права при іксі, що прагнуть плюс нескінченності, ліва при іксі, що прагнуть мінус нескінченності, і двостороння, якщо межі при прагненні ікса до плюс або мінус нескінченності рівні).

Приклад 5.Графік функції

при a> 1 має ліву горизонтальну асимпототу y= 0 (тобто збігається з віссю Ox), так як межа функції при прагненні "ікса" до мінус нескінченності дорівнює нулю:

Правої горизонтальної асимптоти у кривої немає, оскільки межа функції при прагненні "ікса" до плюс нескінченності дорівнює нескінченності:

Похилі асимптоти

Вертикальні та горизонтальні асимптоти, які ми розглянули вище, паралельні осям координат, тому для їх побудови нам потрібна була лише певна кількість - точка на осі абсцис або ординат, через яку проходить асимптота. Для похилої асимптоти необхідно більше – кутовий коефіцієнт k, який показує кут нахилу прямий, та вільний член b, який показує, наскільки пряма знаходиться вище або нижче за початок координат. Не встигли забути аналітичну геометрію, та якщо з неї - рівняння прямої, зауважать, що з похилої асимптоти знаходять рівняння прямої з кутовим коефіцієнтом. Існування похилої асимптоти визначається наступною теоремою, на підставі якої і знаходять названі щойно коефіцієнти.

Теорема.Для того, щоб крива y = f(x) мала асимптоту y = kx + b необхідно і достатньо, щоб існували кінцеві межі kі bрозглянутої функції при прагненні змінної xдо плюс нескінченності та мінус нескінченності:

(1)

(2)

Знайдені в такий спосіб числа kі bі є коефіцієнтами похилої асимптоти.

У першому випадку (при прагненні ікс до плюс нескінченності) виходить права похила асимптота, у другому (при прагненні ікса до мінус нескінченності) - ліва. Права похила асимптота зображена на рис. знизу.

При знаходженні рівняння похилої асимптоти необхідно враховувати прагнення ікса і плюс нескінченності, і мінус нескінченності. У деяких функцій, наприклад, у дробно-раціональних, ці межі збігаються, однак у багатьох функцій ці межі різні і може існувати тільки один з них.

При збігу меж при іксі, що прагне до плюс нескінченності і мінус нескінченності пряма y = kx + b є двосторонньою асимптотою кривою.

Якщо хоча б одна з меж, що визначають асимптоту y = kx + b , немає, то графік функції немає похилої асимптоти (але може мати вертикальну).

Неважко бачити, що горизонтальна асимптота y = bє окремим випадком похилої y = kx + bпри k = 0 .

Тож якщо у якомусь напрямі крива має горизонтальну асимптоту, то цьому напрямі немає похилої, і навпаки.

Приклад 6.Знайти асимптоти графіка функції

Рішення. Функція визначена на всій числовій прямій, крім x= 0, тобто.

Тому в точці розриву x= 0 крива може мати вертикальну асимптоту. Справді, межа функції при прагненні ікса до нуля зліва дорівнює плюс нескінченності:

Отже, x= 0 – вертикальна асимптота графіка цієї функції.

Горизонтальної асимптоти графік цієї функції не має, тому що межа функції при прагненні ікса до плюс нескінченності дорівнює плюс нескінченності:

З'ясуємо наявність похилої асимптоти:

Отримали кінцеві межі k= 2 та b= 0. Пряма y = 2xє двосторонньою похилою асимптотою графіка цієї функції (рис. всередині прикладу).

Приклад 7.Знайти асимптоти графіка функції

Рішення. Функція має одну точку розриву x= −1. Обчислимо односторонні межі та визначимо вид розриву:

Висновок: x= −1 - точка розриву другого роду, тому пряма x= −1 є вертикальною асимптотою графіка цієї функції.

Шукаємо похилі асимптоти. Так як дана функція - дробно-раціональна, межі при і при збігатимуться. Таким чином, знаходимо коефіцієнти для підстановки в рівняння прямої – похилої асимптоти:

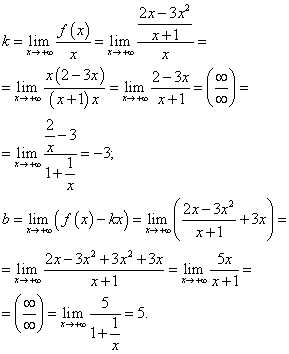
Підставляючи знайдені коефіцієнти рівняння прямої з кутовим коефіцієнтом, отримуємо рівняння похилої асимптоти:

y = −3x + 5 .

На малюнку графік функції позначений бордовим кольором, а асимптоти – чорним.

Приклад 8.Знайти асимптоти графіка функції

Рішення. Оскільки ця функція безперервна, її графік немає вертикальних асимптот. Шукаємо похилі асимптоти:

.

Таким чином, графік цієї функції має асимптоту. y= 0 при і немає асиптоти при .

Приклад 9.Знайти асимптоти графіка функції

Рішення. Спочатку шукаємо вертикальні асимптоти. І тому знайдемо область визначення функції. Функція визначена, коли виконується нерівність і у своїй . Знак змінної xзбігається зі знаком. Тому розглянемо еквівалентну нерівність. З цього отримуємо область визначення функції: . Вертикальна асимптота може бути лише на межі області визначення функції. Але x= 0 може бути вертикальної асимптотою, оскільки функція визначена при x = 0 .

Розглянемо правосторонню межу при (лівостороння межа не існує):

.

Точка, крапка x= 2 – точка розриву другого роду, тому пряма x= 2 - вертикальна асимптота графіка цієї функції.

Шукаємо похилі асимптоти:

Отже, y = x+ 1 - похила асимптота графіка цієї функції при . Шукаємо похилу асимптоту при:

Отже, y = −x − 1 - похила асимптота при .

Приклад 10Знайти асимптоти графіка функції

Рішення. Функція має область визначення . Оскільки вертикальна асимптота графіка цієї функції може бути тільки на межі області визначення, знайдемо односторонні межі функції при .

Саме так формулюється типове завдання, і воно передбачає знаходження ВСІХ асимптот графіка (вертикальних, похилих/горизонтальних). Хоча, якщо бути більш точним у постановці питання - йдеться про дослідження на наявність асимптот (адже таких може взагалі не виявитися).

Почнемо з чогось простого:

Приклад 1

Рішення зручно розбити на два пункти:

1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при , і відразу відомо, що у цій точці функція терпить нескінченний розрив, А пряма, задана рівнянням є вертикальною асимптотою графіка функції . Але перш ніж оформити такий висновок, необхідно знайти односторонні межі:

Нагадую техніку обчислень, на якій я подібно зупинявся у статті безперервність функції. Точки розриву. У вираз під знаком межі замість «Ікс» підставляємо . У чисельнику нічого цікавого:
.

А ось у знаменнику виходить нескінченно мале негативне число:
, Воно і визначає долю межі.

Лівостороння межа нескінченна, і, в принципі, вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього – вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯКрозташований графік функції та побудувати його КОРЕКТНО. Тому обов'язково обчислимо і правосторонню межу:

Висновок: односторонні межі нескінченні, отже, пряма є вертикальною асимптотою графіка функції при .

Перша межа кінцевийОтже, необхідно «продовжити розмову» і знайти другу межу:

Друга межа теж кінцевий.

Таким чином, наша асимптота:

Висновок: Пряма, задана рівнянням є горизонтальною асимптотою графіка функції при .

Для знаходження горизонтальної асимптоти можна користуватися спрощеною формулою:

Якщо існує кінцева межа, то пряма є горизонтальною асимптотою графіка функції.

Неважко помітити, що чисельник та знаменник функції одного порядку зростання, а значить, межа буде кінцевою:

Відповідь:

За умовою не потрібно виконувати креслення, але якщо в самому розпалі дослідження функції, то на чернетці відразу ж робимо малюнок:

Виходячи з трьох знайдених меж, спробуйте самостійно прикинути, як може розташовуватися графік функції. Дуже важко? Знайдіть 5-6-7-8 пікселів і позначте їх на кресленні. Втім, графік цієї функції будується за допомогою перетворень графіка елементарної функції, і читачі, що уважно розглянули Приклад 21 зазначеної статті легко здогадаються, що це за крива.

Приклад 2

Знайти асимптоти графіка функції

Це приклад самостійного рішення. Процес, нагадую, зручно розбити на два пункти – вертикальні асимптоти та похилі асимптоти. У зразку рішення горизонтальна асимптота знайдено за спрощеною схемою.

На практиці найчастіше зустрічаються дробово-раціональні функції, і після тренування на гіперболах ускладнимо завдання:

Приклад 3

Знайти асимптоти графіка функції

Рішення: Раз, два і готове:

1) Вертикальні асимптоти знаходяться у точках нескінченного розриву, тому потрібно перевірити, чи знаменник звертається в нуль. Вирішимо квадратне рівняння :

Дискримінант позитивний, тому рівняння має два дійсні корені, і роботи значно додається =)

З метою подальшого знаходження односторонніх меж квадратний тричлен зручно розкласти на множники:
(Для компактного запису «мінус» внесли в першу дужку). Для підстрахування здійснимо перевірку, подумки або на чернетці розкривши дужки.

Перепишемо функцію у вигляді

Знайдемо односторонні межі в точці:

І в точці:

Таким чином, прямі є вертикальними асимптотами графіка функції, що розглядається.

2) Якщо подивитися на функцію, то цілком очевидно, що межа буде кінцевою і у нас горизонтальна асимптота. Покажемо її наявність коротким способом:

Таким чином, пряма (вісь абсцис) є горизонтальною асимптотою графіка цієї функції.

Відповідь:

Знайдені межі та асимптоти дають чимало інформації про графік функції. Постарайтеся подумки уявити креслення з урахуванням наступних фактів:

Схематично зобразіть вашу версію графіка на чернетці.

Звичайно, знайдені межі однозначно не визначають вид графіка, і можливо, ви припуститеся помилки, але сама вправа надасть неоціненну допомогу в ході повного дослідження функції. Правильна картинка – наприкінці уроку.

Приклад 4

Знайти асимптоти графіка функції

Приклад 5

Знайти асимптоти графіка функції

Це завдання самостійного рішення. Обидва графіки знову володіють горизонтальними асимптотами, які негайно детектуються за такими ознаками: Приклад 4 порядок зростаннязнаменника більше, ніж порядок зростання чисельника, а Прикладі 5 чисельник і знаменник одного порядку зростання. У зразку рішення перша функція досліджена на наявність похилих асимптотів повним шляхом, а друга - через межу .

Горизонтальні асимптоти, на моє суб'єктивне враження, зустрічаються помітно частіше, ніж ті, які «по-справжньому нахилені». Довгоочікуваний загальний випадок:

Приклад 6

Знайти асимптоти графіка функції

Рішення: класика жанру:

1) Оскільки знаменник позитивний, то функція безперервнана всій числовій прямій, і вертикальні асимптоти відсутні. …Чи це добре? Не те слово – чудово! Пункт №1 закрито.

2) Перевіримо наявність похилих асимптотів:

Перша межа кінцевийтому їдемо далі. Під час обчислення другої межі для усунення невизначеності «нескінченність мінус нескінченність»наводимо вираз до спільного знаменника:

Друга межа теж кінцевий, Отже, у графіка аналізованої функції існує похила асимптота:

Висновок:

Таким чином, при графік функції нескінченно близьконаближається до прямої:

Зауважте, що він перетинає свою похилий асимптоту на початку координат, і такі точки перетину цілком допустимі – важливо, щоб «все було нормально» на нескінченності (власне, мова про асимптоти і заходить саме там).

Приклад 7

Знайти асимптоти графіка функції

Рішення: коментувати особливо нічого, тому оформлю приблизний зразок чистового рішення:

1) Вертикальні асимптоти. Досліджуємо точку.

Пряма є вертикальною асимптотою для графіка при .

2) Похилі асимптоти:

Пряма є похилою асимптотою для графіка при .

Відповідь:

Знайдені односторонні межі та асимптоти з високою достовірністю дозволяють припустити, як виглядає графік цієї функції. Коректне креслення наприкінці уроку.

Приклад 8

Знайти асимптоти графіка функції

Це приклад самостійного рішення, зручності обчислення деяких меж можна почленно розділити чисельник на знаменник. І знову, аналізуючи отримані результати, постарайтеся накреслити графік цієї функції.

Вочевидь, що володарями «справжніх» похилих асимптот є графіки тих дробно-раціональних функцій, які мають старший рівень чисельника на одиницю більшестаршого ступеня знаменника. Якщо більше – похилої асимптоти вже не буде (наприклад, ).

Але в житті трапляються й інші чудеса:

Приклад 9

Рішення: функція безперервнана всій числовій прямій, отже, вертикальні асимптоти відсутня. Але похилі цілком можуть бути. Перевіряємо:

Згадую, як ще у ВНЗ зіткнувся зі схожою функцією і просто не міг повірити, що у неї є похила асимптота. До тих пір, доки не обчислив другу межу:

Строго кажучи, тут дві невизначеності: і, але так чи інакше, потрібно використовувати метод рішення, який розібраний у Прикладах 5-6 статті про межі підвищеної складності. Примножуємо і ділимо на сполучене вираз, щоб скористатися формулою:

Відповідь:

Мабуть, найпопулярніша похила асимптота.

Досі нескінченності вдавалося «стригти під одну гребінку», але буває, що графік функції дві різніпохилі асимптоти при і при:

Приклад 10

Дослідити графік функції наявності асимптот

Рішення: підкорене вираз позитивно, значить, область визначення- будь-яке дійсно число, і вертикальних ціпків бути не може.

Перевіримо, чи існують похилі асимптоти.

Якщо «ікс» прагне «мінус нескінченності», то:
(при внесенні "ікса" під квадратний корінь необхідно додати знак "мінус", щоб не втратити негативність знаменника)

Виглядає незвично, але тут невизначеність "нескінченність мінус нескінченність". Примножуємо чисельник і знаменник на поєднане вираз:

Таким чином, пряма є похилою асимптотою графіка при .

З «плюс нескінченністю» все тривіальніше:

А пряма – при.

Відповідь:

Якщо;
якщо .

Не утримаюсь від графічного зображення:

Це одна з гілок гіперболи .

Не рідкість, коли потенційна наявність асимптот спочатку обмежена областю визначення функції:

Приклад 11

Дослідити графік функції наявності асимптот

Рішення: очевидно, що тому розглядаємо тільки праву полуплоскость, де є графік функції.

1) Функція безперервнана інтервалі , отже, якщо вертикальна асимптота існує, це може бути лише вісь ординат. Досліджуємо поведінку функції поблизу точки справа:

Зверніть увагу, тут НІ невизначеності(на таких випадках акцентувалася увага на початку статті Методи вирішення меж).

Таким чином, пряма (вісь ординат) є вертикальною асимптотою для графіка функції при .

2) Дослідження на похилий асимптоту можна провести за повною схемою, але у статті Правила Лопіталми з'ясували, що лінійна функція вищого порядку зростання, ніж логарифмічна, отже: (див. Приклад 1 тієї ж урока).

Висновок: вісь абсцис є горизонтальною асимптотою графіка функції при .

Відповідь:

Якщо;
якщо .

Креслення для наочності:

Цікаво, що у подібної функції асимптот немає взагалі (бажаючі можуть це перевірити).

Два заключні приклади для самостійного вивчення:

Приклад 12

Дослідити графік функції наявності асимптот

Для перевірки на вертикальні асимптоти потрібно спочатку знайти область визначення функції, а потім вирахувати пару односторонніх меж у «підозрілих» точках. Похилі асимптоти теж не виключені, оскільки функція визначена на плюс і мінус нескінченності.

Приклад 13

Дослідити графік функції наявності асимптот

А тут можуть бути тільки похилі асимптоти, причому напрямки слід розглянути окремо.

Сподіваюся, ви знайшли необхідну асимптоту =)

Бажаю успіхів!

Рішення та відповіді:

Приклад 2:Рішення :
. Знайдемо односторонні межі:

Пряма є вертикальною асимптотою графіка функції при .
2) Похилі асимптоти.

Пряма .
Відповідь:

Чертеж до Прикладу 3:

Приклад 4:Рішення :
1) Вертикальні асимптоти. Функція терпить нескінченний розрив у точці . Обчислимо односторонні межі:

Примітка: нескінченно мале негативне число в парній мірі дорівнює нескінченно малому позитивному числу: .

Пряма є вертикальною асимптотою графіка функції.
2) Похилі асимптоти.

Пряма (вісь абсцис) є горизонтальною асимптотою графіка функції при .
Відповідь: . .
Значить, за у графіка немає похилої асимптоти.

Таким чином, пряма є горизонтальною асимптотою графіка даної функції при .
Відповідь: вісь абсцис при .

Вища математика для заочників і не лише >>>

(Перехід на головну сторінку)

Нулі функції. Інтервали знакості функції.

Метод інтервалів

Значна частка матеріалу, що стосується похідних та дослідження функцій, традиційно відноситься до шкільної програми, і ця стаття не є винятком із правила. Сьогодні ми потренуємося в знаходженні нулів та інтервалів знаковості функції, а також докладно розберемо метод інтервалів, який можна порівняти з надійною арматурою в стінах теми, що розглядається.

Якщо проект вашої будівлі знаходиться на стадії котловану, будь ласка, почніть з вступного уроку про графіки функцій. Крім того, бажано ознайомитися зі статтями Область визначення функції, Асимптоти графіка, та, по суті, інформація цієї сторінки – логічне продовження. Матеріал, звичайно, буде корисним і старшокласникам.

У липні 2020 NASA запускає експедицію на Марс. Космічний апарат доставить на Марс електронний носій із іменами всіх зареєстрованих учасників експедиції.

Реєстрація учасників відкрита. Отримайте свій квиток на Марс за цим посиланням.

Якщо цей пост вирішив вашу проблему або просто сподобався вам, поділіться посиланням на нього зі своїми друзями у соціальних мережах.

Один з цих варіантів коду потрібно скопіювати та вставити в код вашої веб-сторінки, бажано між тегами іабо ж відразу після тегу . За першим варіантом MathJax підвантажується швидше і менше гальмує сторінку. Натомість другий варіант автоматично відстежує та підвантажує свіжі версії MathJax. Якщо вставити перший код, його потрібно буде періодично оновлювати. Якщо вставити другий код, то сторінки завантажуватимуться повільніше, зате вам не потрібно буде постійно стежити за оновленнями MathJax.

Підключити MathJax найпростіше в Blogger або WordPress: в панелі керування сайтом додайте віджет, призначений для вставки стороннього коду JavaScript, скопіюйте в нього перший або другий варіант коду завантаження, представленого вище, і розмістіть віджет ближче до початку шаблону (до речі, це зовсім не обов'язково , оскільки скрипт MathJax завантажується асинхронно). От і все. Тепер вивчіть синтаксис розмітки MathML, LaTeX та ASCIIMathML, і ви готові вставляти математичні формули на веб-сторінки свого сайту.

Черговий переддень Нового Року... морозна погода та сніжинки на шибці... Все це спонукало мене знову написати про... фрактали, і про те, що знає про це Вольфрам Альфа. З цього приводу є цікава стаття, в якій є приклади двовимірних фрактальних структур. Тут же розглянемо складніші приклади тривимірних фракталів.

Фрактал можна наочно уявити (описати), як геометричну фігуру або тіло (маючи на увазі, що те й інше є безліч, в даному випадку, безліч точок), деталі якої мають таку ж форму, як і сама вихідна фігура. Тобто, це самоподібна структура, розглядаючи деталі якої при збільшенні, ми бачитимемо ту саму форму, що і без збільшення. Тоді як у випадку звичайної геометричної фігури (не фрактал), при збільшенні ми побачимо деталі, які мають простішу форму, ніж сама вихідна фігура. Наприклад, при досить великому збільшенні частина еліпса виглядає як відрізок прямий. З фракталами такого не відбувається: при будь-якому їх збільшенні ми знову побачимо ту саму складну форму, яка з кожним збільшенням повторюватиметься знову і знову.

Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки про фрактали, у своїй статті Фрактали та мистецтво в ім'я науки написав: "Фрактали - це геометричні форми, які однаково складні у своїх деталях, як і у своїй загальній формі. Тобто якщо частина фракталу буде збільшена до розміру цілого, вона виглядатиме, як ціле, або точно, або, можливо, з невеликою деформацією".

Якщо відстань d від точки кривої у = f (х), що має нескінченну гілку, до певної певної прямої в міру видалення точки по цій кривій в нескінченність прагне нуля, то пряма називається асимптотою кривої.

Розрізняють асимптоти: 1) горизонтальні, 2) вертикальні та 3) похилі.

1. Крива у = f (х) має горизонтальну асимптоту у = b тільки в тому випадку, коли існує кінцева межа функції f (х) при , і ця межа дорівнює b , тобто якщо

2. Крива у = f (х) має вертикальну асимптоту х = а якщо при . Для визначення вертикальних асимптот треба знайти ті значення аргументу, поблизу яких f(х) необмежено збільшується за абсолютною величиною. Якщо такими значеннями аргументу є а1, а2, …, то рівняння вертикальних асимптот будуть

х = а1, х = а2 ...

3. Для визначення похилої асимптоти у = kx + b кривою у = f(х) треба знайти числа k та b з формул

(Слід окремо розглядати випадки). Похилі асимптоти у кривої у = f(х) існують у тому і лише в тому випадку, коли ці межі мають кінцеве значення. При визначенні цих меж зручно скористатися правилом Лопіталя.

приклад. Знайти асимптоти кривої

Рішення. Горизонтальних асимптотів немає. Вертикальну асимптоту знаходимо з умови

2х + 3 = 0 => х = - 3/2, при цьому у
, коли
, у
, коли
. Визначимо похилі асимптоти, рівняння яких має вигляд: у = kx + b

Оскільки k і b мають кінцеві значення та рівні між собою при х
і при х
, то є єдина похила асимптота, рівняння якої

Загальне дослідження функції

Під повним дослідженням функції зазвичай розуміється вирішення таких питань:

Визначення сфери існування функції.

Виявлення питання про парність та непарність функції.

Визначення точок розриву функції.

Визначення асимптоту графіка функції.

Визначення інтервалів зростання та зменшення функції.

Визначення екстремуму функції.

Визначення інтервалів опуклості та увігнутості графіка функції.

Визначення точок перегину.

Знаходження перетину з осями координат.

Побудова графіка функції.

приклад. Досліджуємо функцію

D(y) = (
). Функція безперервна по всій області визначення. Точок розриву немає.

Функція не є ні парною, ні непарною, ні періодичною.

Точок розриву немає.

Вертикальних асимптотів немає;
, похилих асимптотів немає.

5, 6.
. Критичні точки x = -2, x = 0.

7, 8.
,
при х = 1,
не існує за х = 0.

9.
х = 0 і х = -5.

Завдання 1

Обчислити визначник матриці А другого порядку

Обчислити визначник матриці третього порядку

Обчислити визначник матриці В, розклавши його по будь-якому рядку і якомусь стовпцю

Обчислити визначник матриці, користуючись властивостями визначників. Звести обчислення визначника третього порядку до обчислення одного визначника другого порядку

Завдання 2

1. Вирішити методом Крамера систему рівнянь Ах = а

Розв'язати методом Крамера систему рівнянь Вx = b

Розв'язати методом Гауса систему рівнянь Вx = b

Завдання 3.

Ах = а

Розв'язати матричним методом систему рівнянь Вx = b

Завдання 4.

Обчислити ранг матриці.

1., 2.
;

3.
4.

5.
6.

7.
8

9.
10.

Завдання 5

Дано дві вершини трикутника Δ АВС: А (х 1 ,у 1 ), В(х 2 ,у 2 ) і крапка D (x 3 , y 3 )перетину висот:

а) скласти рівняння висот, медіан, бісектрис трикутника Δ АВС.

б) знайти рівняння прямих, що проходять через вершини трикутника та паралельних сторонам.

в) визначити довжини висот трикутника та відстань від точки М (х 4 , у 4 ) до сторін трикутника.

Завдання 6.

Дано координати вершин піраміди АВСD: А (х 1 ,у 1 , z 1 ), В(х 2 ,у 2 , z 3 ) ,C (x 2 , y 2 , z 2 ) ,D (х 4 , у 4 , z 3 )

1) довжину ребра АВ;.

2) кут між ребрами АВі АD;

3) кут меду руба AD та гранню ABC;

4) площа грані ABC;

5) обсяг піраміди;

6) рівняння прямої AB;

7) рівняння площини ABC;

8) рівняння висоти, опущеної з вершини Dна межу ABC.

Завдання 7.

Завдання 8. Знайти область визначення функції

5.

7.

8.

9.

10.

Завдання 9. Побудувати графік функції

1.

2.

3.

4

5.

6.

7.

8.

9.

10.

Завдання 10. Знайти межі функції

1.а)
, б)
, в)
,

г)
д)

2.а)
, б)
, в)
,

г)
д)

3.а)
, б)
, в)
,

г)
д)

4. а)
, б)
, в)
,

г)
д)

5.а)
, б)
, в)
,

г)
д)

6.а)
, б)
, в)
,

г)
д)

7. а)
, б)
, в)
,

г)
д)

8.а)
, б)
, в)
,

г)
д)

9.а)
, б)
, в)
,

г)
д)

10.а)
, б)
, в)
,

г)
д)

Завдання 11. Знайти похідну

1.
, б),

в)
, г)
д)
, е)

2. а)
, б)
, в)
,

г)
д)
,е)

3. а), б)
, в)
, г)
д)
, e)

4. а)
, б)
, в)
,

г)
д)
, e)

5. а)
, б)
, в)
, г)
д)
,

е)

6. а)
, б)
, в)
, г)
д)
,

е)

7. а)
, б),

в)
, г)
д)
,

е)

8. а)
, б)
, в)
, г)
д)
,

е)

9. а)
, б)
, в)
,

г)
д)
, е)

10. а)
, б)
, в)
,

г)
д)
, е)

Завдання 12. Показати, що функція задовольняє рівності

Завдання 13. Знайти другу похідну функцію, задану параметрично.

1 .
6.

2.
7

3.
8

4.
9.

5.
10.

Завдання 14. Знайти межі, користуючись правилом Лопіталю

Завдання 15. Знайти екстремуми заданих функцій.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Завдання 16. Знайти найбільше та найменше значення на вказаних відрізках та на вказаних інтервалах.

Завдання 17. Провести повне дослідження цих функцій та накреслити їх графіки.

1.
6.

2.
7.

3.
8.

4.
9.

5.
10.

Література:

Баврін І.І. Курс вищої математики.-М.: Просвітництво, 1992.-400 с.

Бронштейн І.М., Семендяєв К.А. Довідник математики. М, 1967г, 608 з

Загальний курс вищої математики для економістів, за ред. В.І.Єрмакова-М. «Інфра-М». 1999-655 с.

Теуш В.Л. Курс найвищої математики. - М: Радянська наука, 1958р, 270 с.

Шипачов В.С. Вища математика: Навчальний посібник М. Вища школа, 1990-479с.

Вища математика для економістів: Підручник для вузів/Н.Ш.Кремер, Б.А.Путко та ін.; М: ЮНІТІ, 2002. - 461 с.

Валєєв К.Г, Джалладова І.А Вища математика: Навч. Посібник.

Асимптоти графіка функції

Примара асимптоти давно бродила сайтом щоб, нарешті, матеріалізуватися в окремо взятій статті і привести в особливе захоплення читачів, спантеличених повним дослідженням функції. Знаходження асимптот графіка – одна з небагатьох частин зазначеного завдання, що висвітлюється у шкільному курсі лише в оглядовому порядку, оскільки події обертаються навколо обчислення меж функцій, А вони відносяться все-таки до вищої математики. Відвідувачі, які слабо знаються на математичному аналізі, натяк, думаю, зрозумілий;-) …стоп-стоп, ви куди? Межі- це легко!

Приклади асимптот зустрілися відразу на першому уроці про графіки елементарних функцій, і зараз тема отримує детальний розгляд.

Що таке асимптота?

Уявіть змінну точку, Що «їздить» за графіком функції. Асимптота – це пряма, до якої необмежено близьконаближається графік функції при видаленні його змінної точки в нескінченність.

Примітка : визначення змістовно, якщо вам потрібне формулювання в позначеннях математичного аналізу, будь ласка, зверніться до підручника.

На поверхні асимптоти класифікують за їх природним розташуванням:

1) Вертикальні асимптоти, Які задаються рівнянням виду , Де «альфа» - дійсне число. Популярна представниця визначає саму вісь ординат,
з приступом легкої нудоти згадуємо гіперболу.

2) Похилі асимптотитрадиційно записуються рівнянням прямоїз кутовим коефіцієнтом. Іноді окремою групою виділяють окремий випадок. горизонтальні асимптоти. Наприклад, та ж гіпербола з асимптотою.

Швидко пішло-поїхало, вдаримо по темі короткою автоматною чергою:

Скільки асимптот може мати графік функції?

Жодної, одна, дві, три, або нескінченно багато. За прикладами далеко ходити не будемо, згадаємо елементарні функції. Парабола, кубічна парабола, синусоїда зовсім не мають асимптоту. Графік експоненційної, логарифмічної функції має єдину асимптоту. У арктангенса, арккотангенса їх дві, а тангенса, котангенса – нескінченно багато. Не рідкість, коли графік укомплектований і горизонтальними та вертикальними асимптотами. Гіпербола, буде завжди love you.

Що означає ?

Вертикальні асимптоти графіка функції

Вертикальна асимптота графіка, як правило, знаходиться у точці нескінченного розривуфункції. Все просто: якщо в точці функція зазнає нескінченного розриву, то пряма, задана рівнянням є вертикальною асимптотою графіка.

Примітка : Зверніть увагу, що запис використовується для позначення двох абсолютно різних понять. Точка має на увазі або рівняння прямої - залежить від контексту.

Таким чином, щоб встановити наявність вертикальної асимптоти в точці, достатньо показати, що хоча б одинз односторонніх меж нескінченний. Найчастіше це точка, де знаменник функції дорівнює нулю. Фактично, ми вже знаходили вертикальні асимптоти в останніх прикладах уроку про безперервність функції. Але в ряді випадків існує тільки одна одностороння межа, і, якщо вона нескінченна, то знову - любіть і шануйте вертикальну асимптоту. Найпростіша ілюстрація: і вісь ординат (див. Графіки та властивості елементарних функцій).

З вищесказаного також випливає очевидний факт: якщо функція безперервна на, то вертикальні асимптоти відсутні. На думку чомусь спала парабола. Справді, де тут «устромиш» пряму? …так… розумію… послідовники дядечка Фрейда забилися в істериці =)

Зворотне твердження в загальному випадку неправильне: так, функція не визначена на всій числовій прямій, але абсолютно обділена асимптотами.

Похилі асимптоти графіка функції

Похилі (як окремий випадок – горизонтальні) асимптоти можуть намалюватися, якщо аргумент функції прагне «плюс нескінченності» або «мінус нескінченності». Тому графік функції не може мати більше двох похилих асимптот. Наприклад, графік експоненціальної функції має єдину горизонтальну асимптоту при , а графік арктангенса при – два такі асимптоти, причому різні.

Коли графік і там і там зближується з єдиною похилою асимптотою, то «нескінченності» прийнято поєднувати під єдиним записом. Наприклад, …правильно здогадалися: .

Загальне практичне правило:

Якщо існують два кінцевихмежі то пряма є похилою асимптотою графіка функції при . Якщо хоча б одинз перелічених меж нескінченний, то похила асимптота відсутня.

Примітка : формули залишаються справедливими, якщо «ікс» прагне тільки «плюс нескінченності» або тільки «мінус нескінченності»

Покажемо, що парабола не має похилих асимптотів:

Межа нескінченна, отже, похила асимптота відсутня. Зауважте, що у знаходженні межі необхідність відпала, оскільки відповідь вже отримано.

Примітка : якщо у вас виникли (або виникнуть) труднощі з розумінням знаків «плюс-мінус», «мінус-плюс», будь ласка, перегляньте довідку на початку уроку
про нескінченно малі функціїде я розповів, як правильно інтерпретувати дані знаки.

Очевидно, що у будь-якої квадратичної, кубічної функції, багаточлена 4-го та вищих ступенів також немає похилих асимптот.

А тепер переконаємося, що при графіку теж немає похилої асимптоти. Для розкриття невизначеності використовуємо правило Лопіталя:
, Що й потрібно перевірити.

При функція необмежено зростає, проте не існує такої прямої, до якої б її графік наближався нескінченно близько.

Переходимо до практичної частини уроку:

Як знайти асимптоти графіка функції?

Саме так формулюється типове завдання, і воно передбачає знаходження ВСІХ асимптот графіка (вертикальних, похилих/горизонтальних). Хоча, якщо бути більш точним у постановці питання – йдеться про дослідження на наявність асимптот (адже таких може взагалі не виявитися). Почнемо з чогось простого:

Приклад 1

Знайти асимптоти графіка функції

Рішеннязручно розбити на два пункти:

1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при , і відразу відомо, що у цій точці функція терпить нескінченний розрив, А пряма, задана рівнянням є вертикальною асимптотою графіка функції . Але перш ніж оформити такий висновок, необхідно знайти односторонні межі:

Нагадую техніку обчислень, на якій я подібно зупинявся у статті Безперервність функції. Точки розриву. У вираз під знаком межі замість «Ікс» підставляємо . У чисельнику нічого цікавого:
.

А ось у знаменнику виходить нескінченно мале негативне число:
, Воно і визначає долю межі.

Лівостороння межа нескінченна, і, в принципі, вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього – вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯКрозташований графік функції та побудувати його КОРЕКТНО. Тому обов'язково обчислимо і правосторонню межу:

Висновок: односторонні межі нескінченні, отже, пряма є вертикальною асимптотою графіка функції при .

Перша межа кінцевийОтже, необхідно «продовжити розмову» і знайти другу межу:

Друга межа теж кінцевий.

Таким чином, наша асимптота:

Висновок: Пряма, задана рівнянням є горизонтальною асимптотою графіка функції при .

Для знаходження горизонтальної асимптоти
можна користуватися спрощеною формулою:

Якщо існує кінцевиймежа, то пряма є горизонтальною асимптотою графіка функції при.

Неважко помітити, що чисельник та знаменник функції одного порядку зростання, а значить, межа буде кінцевою:

Відповідь:

За умовою не потрібно виконувати креслення, але якщо в самому розпалі дослідження функції, то на чернетці відразу ж робимо малюнок:

Виходячи з трьох знайдених меж, спробуйте самостійно прикинути, як може розташовуватися графік функції. Дуже важко? Знайдіть 5-6-7-8 пікселів і позначте їх на кресленні. Втім, графік цієї функції будується за допомогою перетворень графіка елементарної функції, і читачі, що уважно розглянули Приклад 21 зазначеної статті легко здогадаються, що це за крива.

Приклад 2

Знайти асимптоти графіка функції

Це приклад самостійного рішення. Процес, нагадую, зручно розбити на два пункти – вертикальні асимптоти та похилі асимптоти. У зразку рішення горизонтальна асимптота знайдено за спрощеною схемою.

На практиці найчастіше зустрічаються дробово-раціональні функції, і після тренування на гіперболах ускладнимо завдання:

Приклад 3

Знайти асимптоти графіка функції

Рішення: Раз, два і готове:

1) Вертикальні асимптоти знаходяться у точках нескінченного розриву, тому потрібно перевірити, чи знаменник звертається в нуль. Вирішимо квадратне рівняння:

Дискримінант позитивний, тому рівняння має два дійсні корені, і роботи значно додається =)

З метою подальшого знаходження односторонніх меж квадратний тричлен зручно розкласти на множники:
(Для компактного запису «мінус» внесли в першу дужку). Для підстрахування здійснимо перевірку, подумки або на чернетці розкривши дужки.

Перепишемо функцію у вигляді

Знайдемо односторонні межі в точці:

І в точці:

Таким чином, прямі є вертикальними асимптотами графіка функції, що розглядається.

2) Якщо подивитися на функцію , то цілком очевидно, що межа буде кінцевою і у нас горизонтальна асимптота. Покажемо її наявність коротким способом:

Таким чином, пряма (вісь абсцис) є горизонтальною асимптотою графіка цієї функції.

Відповідь:

Знайдені межі та асимптоти дають чимало інформації про графік функції. Постарайтеся подумки уявити креслення з урахуванням наступних фактів:

Схематично зобразіть вашу версію графіка на чернетці.

Звичайно, знайдені межі однозначно не визначають вид графіка, і можливо, ви припуститеся помилки, але сама вправа надасть неоціненну допомогу в ході повного дослідження функції. Правильна картинка – наприкінці уроку.

Приклад 4

Знайти асимптоти графіка функції

Приклад 5

Знайти асимптоти графіка функції

Це завдання самостійного рішення. Обидва графіки знову володіють горизонтальними асимптотами, які негайно детектуються за такими ознаками: Приклад 4 порядок зростаннязнаменника більше, ніж порядок зростання чисельника, а Прикладі 5 чисельник і знаменник одного порядку зростання. У прикладі рішення перша функція вивчена на наявність похилих асимптот повним шляхом, а друга – через межу .

Горизонтальні асимптоти, на моє суб'єктивне враження, зустрічаються помітно частіше, ніж ті, які «по-справжньому нахилені». Довгоочікуваний загальний випадок:

Приклад 6

Знайти асимптоти графіка функції

Рішення: класика жанру:

1) Оскільки знаменник позитивний, то функція безперервнана всій числовій прямій, і вертикальні асимптоти відсутні. …Чи це добре? Не те слово – чудово! Пункт №1 закрито.

2) Перевіримо наявність похилих асимптотів:

Перша межа кінцевийтому їдемо далі. Під час обчислення другої межі для усунення невизначеності «нескінченність мінус нескінченність»наводимо вираз до спільного знаменника:

Друга межа теж кінцевий, Отже, у графіка аналізованої функції існує похила асимптота:

Висновок:

Таким чином, при графік функції нескінченно близьконаближається до прямої:

Зауважте, що він перетинає свою похилий асимптоту на початку координат, і такі точки перетину цілком допустимі – важливо, щоб «все було нормально» на нескінченності (власне, мова про асимптоти і заходить саме там).

Приклад 7

Знайти асимптоти графіка функції

Рішення: коментувати особливо нічого, тому оформлю приблизний зразок чистового рішення:

1) Вертикальні асимптоти. Досліджуємо точку.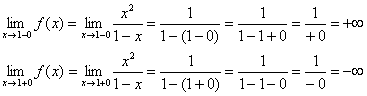

Пряма є вертикальною асимптотою для графіка при .

2) Похилі асимптоти:

Пряма є похилою асимптотою для графіка при .

Відповідь:

Знайдені односторонні межі та асимптоти з високою достовірністю дозволяють припустити, як виглядає графік цієї функції. Коректне креслення наприкінці уроку.

Приклад 8

Знайти асимптоти графіка функції

Це приклад самостійного рішення, зручності обчислення деяких меж можна почленно розділити чисельник на знаменник. І знову, аналізуючи отримані результати, постарайтеся накреслити графік цієї функції.

Вочевидь, що володарями «справжніх» похилих асимптот є графіки тих дробно-раціональних функцій, які мають старший рівень чисельника на одиницю більшестаршого ступеня знаменника. Якщо більше – похилої асимптоти не буде (наприклад, ).

Але в житті трапляються й інші чудеса:

Приклад 9

Приклад 11

Дослідити графік функції наявності асимптот

Рішення: очевидно, що тому розглядаємо тільки праву напівплощину, де є графік функції.

Таким чином, пряма (вісь ординат) є вертикальною асимптотою для графіка функції при .

2) Дослідження на похилий асимптоту можна провести за повною схемою, але у статті Правила Лопіталями з'ясували, що лінійна функція вищого порядку зростання, ніж логарифмічна, отже: (Див. Приклад 1 того ж уроку).

Висновок: вісь абсцис є горизонтальною асимптотою графіка функції при .

Відповідь:
, якщо;
якщо .

Креслення для наочності:

Цікаво, що у подібної функції асимптот немає взагалі (бажаючі можуть це перевірити).

Два заключні приклади для самостійного вивчення:

Приклад 12

Дослідити графік функції наявності асимптот