Похідні зворотних тригонометричних функцій. Похідні простих тригонометричних функцій Похідні зворотних тригонометричних функцій визначення
тема :
Ціль : Сформувати уявлення про похідні зворотні тригонометричні функції.
Завдання:
1.
навчити знаходити похідні даних функцій,відпрацювати з учнями вміння диференціювати дані функції за допомогою
самостійної роботи та взаємоперевірки;
2.
розвивати інтерес до математики, обчислювальні тапізнавальні навички,
вміння аналізувати помилки інших учнів;
3. виховувати уважність, самостійність
1. Організаційний момент
Вітаю учнів, знайомлю з правилами роботи на уроці, пояснюю, як правильно заповнювати рейтинговий лист
2. Мотиваційний етап
Учні читають обов'язково, що вони повинні знати та вміти на цю тему.
Перед початком роботи ознайомтеся з правилом ПАМ'ЯТКИ.
3.Операційний етап
Учні приступають до виконання завдань з навчального листа (додається)
4.Підсумок уроку
Рефлексія.
Сьогодні на уроці:
Я впізнав…
Було цікаво…
Було тяжко…
У мене вийшло…
Я спробую…
НАВЧАЛЬНЕ ЛИСТ
по темі: Похідні тригонометричних та зворотних тригонометричних функцій.
2 уроки.
В РЕЗУЛЬТАТІ ВИВЧЕННЯ ТЕМИ ПОТРІБНО
ЗНАТИ: формули диференціювання для тригонометричних та зворотних тригонометричних функцій.
ВМІТИ: знаходити похідні тригонометричних та зворотних тригонометричних функцій.
Пам'ятай , що треба працювати за алгоритмом.
Не забувай проходити перевірку, робити позначки на полях, заповнювати рейтинговий лист теми.
Будь ласка, не залишай без відповіді, що виникли у тебе питання.
Будь об'єктивним під час взаємоперевірки, це допоможе і тобі, і тому, кого ти перевіряєш.
БАЖАЮ УСПІХУ!
З АДАННЯ №1
Прочитай та вивчи формули диференціювання зворотних тригонометричних функцій: (2 б.)
Якщо функція складна, то
де z – елементарна функція
Розглянь приклади:
y = arcsin(x) тоді y/=
y = arcctg(3x 2 -4) тоді
y/=
Знайди похідні:(3 б.)
y= arcsin(-x) y = arctg(-x) y = arcos(2x)
П ЗАЙДИ ПЕРЕВІРКУ №1
З АДАННЯ №2
Розв'яжи будь-який із прикладів: (3б)
а ) y = arcos (5x - 3)
б ) y = arcctg(7x+1)
П ЗАЙДИ ПЕРЕВІРКУ №2
З АДАННЯ №3
а) Розглянь ще раз рішення прикладу:
б) Знайди похідні функції (4 б.)
arcsin(2x 2 - 5x)
arccos(4x 2 - 6x)
П ЗАЙДИ ПЕРЕВІРКУ №3
З АДАННЯ №4
Молодець! Можна приступити доперевірочній роботі №1.
ЗАВДАННЯ №5
а) Розглянь рішення прикладу:
б) Знайди похідні функції (6 б.)
y =
П ЗАЙДИ ПЕРЕВІРКУ №5
Молодець! Можна приступити доперевірочній роботі №2.
ПРОВІРКОВА РОБОТА №1
Виконай один з варіантів (11б)
1в 2в
1.Знайди похідні наступних функцій:
а) 2 бали
y = arctg(-2x) y = arcos(3x)
б) 4 бали
y = arcos(3x 2 - 2) y = arcctg(2x 3 +1)
в) 5 балів
y = arcsin(x 2 - 5x) + tg (2x+1) y = arccos(3x 2 - 2x) + ctg(x+4) Мах
балів
отриманий
бал
хто
перевірив
оцінка
1
2 б
3 б
2
3б
3
4б
4
1 1 б
5
6 б
6
1 4 б
разом
43 б
РАЗОМ 43 бали
"5" - 33 - 43 бали;
«4» - 24 – 32 бали;
"3" - 18 - 23 бали.
Диференціальне обчислення функції однієї змінної
1. Вступ
Математичний аналіз - галузь математики, що оформилася в ХVIII столітті і включає дві основні частини: диференціальне та інтегральне обчислення. Похідна функції – одне з основних математичних понять диференціального обчислення. Аналіз виник завдяки зусиллям багатьох математиків (насамперед І. Ньютона і Р. Лейбніца) і зіграв величезну роль розвитку природознавства – з'явився потужний, досить універсальний метод дослідження функцій, що виникають під час вирішення різноманітних прикладних завдань.
2. Числова функція. Схема дослідження функції.
(Дивись конспекти на тему «Ступінна функція»)
1) Область визначення функції.
2) Безліч значень функції.
3) парність, непарність функції.
4) Монотонність функції.
5) Оборотність функції.
6) Нулі функції.
7) Проміжки знаковості функції.
8) Обмеженість функції.
Вправи:
- Знайти область визначення функції:
а); б); в) ![]() .
.
а); б); г).
3. Поняття межі функції у точці.
Розглянемо графіки деяких функцій. Вивчимо поведінку функцій поблизу точки х 0 , тобто в деякій околиці точки х 0 .
 |
Рис. 1. Мал. 2. Мал. 3.
Функція має властивість, що відрізняє її від двох інших функцій.
1. При наближенні аргументу хдо х 0ліворуч і праворуч відповідні значення функції як завгодно близькі до одного і того ж числа А.
Цією властивістю не мають дві інші функції.
2. При наближенні аргументу хдо х 0ліворуч відповідні значення функції як завгодно близькі до А, а при наближенні аргументу хдо х 0праворуч відповідні значення функції як завгодно близькі до В.
3. Функція при наближенні аргументу хдо х 0ліворуч і праворуч приймає різні значення.
Висновок: Якщо при наближенні аргументу х до х 0 ліворуч і праворуч точки з координатами як завгодно близькі до точки з координатами, то.
Приклад: Чи має функція межа в точках х 1, х 2, х 3, х 4, х 5?
 |
Відповідь: Функція має межу в точках х1, х3;
функція не має межі в точках х2, х4, х5.
Зауваження:
![]()
4. Визначення функції безперервної у точці та на проміжку
Поняття безперервності функції зручно пов'язати з уявленням про графік цієї функції як про «нерозривну» (суцільну) лінію. Суцільною лінією вважатимемо лінію, накреслену без відриву олівця від паперу.
Питання: Які з цих функцій є безперервними?

 Рис. 1. Мал. 2. Мал. 3.
Рис. 1. Мал. 2. Мал. 3.
Рис. 4. Мал. 5.
Відповідь: З цих функцій безперервною є функція, зображена на рис. №3, оскільки її графік – «нерозривна» (суцільна) лінія.
Питання: Які властивості має функція, зображена на рис. №3, і не мають інших функцій?
Відповідь:
1. Функція визначена у точці х 0 . Ця властивість не виконується для функції, зображеної на рис. №1.
2. Існує кінцева межа функції у точці х 0 . Ця властивість не виконується для функцій, зображених на рис. №2, 5.
3. Межа функції у точці х 0 дорівнює значенню функції у цій точці, тобто ![]() . Ця властивість не виконується для функції, зображеної на рис. №4.
. Ця властивість не виконується для функції, зображеної на рис. №4.
Властивості, що виконуються для функції, зображеної на рис. №3, і дають можливість дати визначення безперервної функції в точці х 0 .
Визначення: Функція називається безперервною у точці х 0, якщо ![]() .
.
Зауваження: Якщо функція є безперервною у точці х 0, то точка х 0 називається точкою безперервності функції, якщо функція не є безперервною у точці х 0, то точка х 0 називається точкою розриву функції.
 Визначення:
Функція називається безперервною на інтервалі, якщо вона безперервна у кожній точці цього інтервалу.
Визначення:
Функція називається безперервною на інтервалі, якщо вона безперервна у кожній точці цього інтервалу.
5. Приріст аргументу, прирощення функції
Нехай задана функція .
х 0 –початкове значення аргументу;
х-кінцеве значення аргументу;
f (х 0) -початкове значення функції;
f(х 0 +D х) -кінцеве значення функції.
Визначення: Різниця кінцевого та початкового значень аргументу називається збільшенням аргументу D х = х - х 0
Визначення: Різниця кінцевого та початкового значень функції називається збільшенням функції. D у = f(х 0 + D х) - f (х 0)
Зауваження:
- Геометрично збільшення аргументу D х- є різниця абсцис точок графіка функції, що відповідають кінцевому та початковому значенням аргументу.
- Геометрично збільшення функції D у- є різниця ординат точок графіка функції, що відповідають кінцевому та початковому значенням аргументу.
- Приріст аргументу і збільшення функції можуть бути як позитивними, так і негативними.
6. Поняття похідної функції. Фізичний сенс похідної функції
Розглянемо задачу про швидкість зміни функції , де х і у можуть бути будь-якими фізичними величинами.
х 0 –початкове значення аргументу; f (х 0) - початкове значення функції;
х 0 +D х –кінцеве значення аргументу; f(х 0 +D х) - кінцеве значення функції;
D у = f(х 0 + D х) - f (х 0) -збільшення функції;

![]()
– середня швидкість зміни функції на інтервалі D х .
– миттєва швидкість зміни функції, швидкість зміни функції у точці х 0.
Визначення: Похідні функції в точці х 0називається межа відношення збільшення D уфункції у точці х 0до збільшення D харгументу при прагненні збільшення аргументу до нуля.
![]()
Висновок: Похідна функції в точці х 0є швидкість зміни функції у точці х 0.
Теорема: Похідна постійної функції у = су будь-якій точці дорівнює нулю.
Теорема: Похідна функції у = ху будь-якій точці дорівнює одиниці .
.
Зауваження: Знаходження похідної від цієї функції називається диференціюванням.
7. Правила диференціювання суми, твору, приватної функції
Розглянемо функцію , що складається з двох інших функцій і мають похідні на відрізку :
3) ![]() .
.
Теорема №1: Похідна суми (різниці) двох функцій дорівнює сумі (різниці) похідних цих функцій ![]()
Приклад: Обчислити похідну функції
Теорема №2: Похідна робота двох функцій визначається за формулою:
![]()
Слідство: Постійний множник можна винести за знак похідної: .
Доказ: .
Приклад
Вправи:
2) ![]() ;
;
Похідна статечної функції обчислюється за формулою:
Зауваження:
Формула справедлива для статечної функції з будь-яким показником ступеня. ![]() ,
,
Приклад: Обчислити похідні функцій:
Висновок:  .
.
Вправи: Обчислити похідні функцій:
| 1) | 4) ; 5) ; | 6) ; 7) . |
Теорема №3: Похідна приватного двох функцій визначається за формулою:

Наслідки: ;
Приклад: Обчислити похідні функцій:

2) . .
3) .  .
.
Вправи: Обчислити похідні функцій:
| 1. ; 2. ; 3. ; | 4. ;
5. ;
6. | 7. |
8. Поняття складної функції
Правило диференціювання складної функції
Нехай функція визначена на множині, а функція на множині, причому для, відповідне значення. Тоді на безлічі визначено функцію, яка називається складною функцією від х (функцією від функції).
Змінну називають проміжним аргументом складної функції.
Приклад:
Вправи:
- З яких елементарних функцій складаються ці складні функції:
| 1) ; 2) ; | 3) |
- З цих елементарних функцій скласти складні функції:
| 1) , ; 2) , ; | 3) , . 4) , , . |
Висновок: Похідна складної функції дорівнює добутку похідних елементарних функцій, її складових. .
Приклад: Обчислити похідні функцій:
- статечна, лінійна; , .
- статечна, квадратична; , .
![]() .
.
Вправи: Обчислити похідні функцій:
| 1. ;
2. | 3. ; 4. ; | 5. |
9. Похідна показової, логарифмічної функцій
![]()
![]()
Приклад: Обчислити похідні функцій:
1. . ![]() .
.
2. . ![]() .
.
3. . ![]() .
.
Приклад: Обчислити похідні функцій:
1. . ![]() .
.
2. . ![]() .
.
Вправи: Обчислити похідну функції:
| 1. ; 2. ; 3. ; | 4. ; 5. ; 6. ; | 7. ; 8. . |
10. Похідні тригонометричних функцій
Похідні зворотних тригонометричних функцій
![]() .
.
Приклад: Обчислити похідні функцій:
1. ![]() . .
. .
2. . .
Завдання
. ![]() .
.
Завдання: Обчислити похідну функції .

![]() .
.
Вправа: Обчислити похідну функції .
Похідні зворотних тригонометричних функцій
| | |
Вправи: Обчислити похідні функцій:
| 1.
2. | 5.
6.
7.
8.
9. | 10. |
11.  Геометричний сенс похідної функції
Геометричний сенс похідної функції
Розглянемо функцію.
На графіку функції візьмемо фіксовану точку та довільну точку . Проведемо січну . Якщо точку М необмежено наближати до точки М 0 за графіком функції , то січна М 0 М буде займати різні положення та при збігу точки М з точкою М 0 січна займе граничне положення М 0 Т тоді пряма М 0 Т буде дотичною до графіку функції у точці М 0 .
Визначення: Стосується графіка функції у точці М 0називається граничне становище М 0 Тсікучою при прагненні точки Мза графіком до точки М0.
b- кут нахилу сіючої М 0 М
a-кут нахилу дотичної М 0 Т до позитивного напрямку осі абсцис.
Кутовий коефіцієнт січної М 0 М .
Кутовий коефіцієнт дотичної М 0 Т .
Розглянемо прямокутний трикутник М 0 МА
(![]() ). Тангенс гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до прилеглого:
). Тангенс гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до прилеглого: ![]()
Тобто ![]() . А значить,
. А значить, ![]() .
.
Визначимо похідну функції у точці х 0
: ![]() .
.
![]() ,
, ![]() , отже,
, отже, ![]() .
.
Висновок: Геометричний сенс похідної функції полягає в тому, що похідна функції при дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції в точці з абсцисою.
![]()
Приклад:
1. Знайти кутовий коефіцієнт дотичної, проведеної до графіка функції у точках ![]() .
.
![]() ;
; ![]() ; ; ; ; .
; ; ; ; .
Відповідь: ; ; .
2. Знайти кут нахилу дотичної, проведеної до графіку функції у точці з абсцисою.
![]() ;
; ![]() ; ; ; .
паралельна прямий;
; ; ; .
паралельна прямий;
Встановимо необхідну умову існування екстремуму.
Теорема Ферма: Якщо внутрішня точка х 0з області визначення безперервної функції є точкою екстремуму і в цій точці існує похідна, вона дорівнює нулю.
Зауваження: Однак рівність нуля похідної функції у точці х 0 ще не дає права стверджувати, що х 0 – точка екстремуму функції.
II семестр
- Ознаки зростання та зменшення функції. Теорема Лагранжа.
Визначення зростаючої функції.
Функція y = f(x) зростає на інтервалі X, якщо для будь-яких і ![]() виконується нерівність. Іншими словами – більшого значення аргументу відповідає більше значення функції.
виконується нерівність. Іншими словами – більшого значення аргументу відповідає більше значення функції.
Визначення спадної функції.
Функція y = f(x) зменшується на інтервалі X, якщо для будь-яких і ![]() виконується нерівність. Інакше кажучи – більшого значення аргументу відповідає менше значення функції.
виконується нерівність. Інакше кажучи – більшого значення аргументу відповідає менше значення функції.

Теорема Лагранжа: Скористаємося геометричним змістом похідної, щоб дати наочні пояснення справедливості того, що існує дотична до графіка f у точці з абсцисою з інтервалу (а; b), паралельна січній, що проходить через точки A (a; f (а)), (b; f (b)).
Розглянемо пряму l, паралельну АВ і не має загальних точок із частиною графіка, що відповідає проміжку [а; b]. Переміщатимемо цю пряму l у напрямку до графіка f так, щоб вона залишалася паралельною АВ. Зафіксуємо положення l 0 цієї прямої в той момент, коли в неї з'являться загальні точки з цією частиною графіка.
 З рис.1 видно, що кожна з таких «перших» загальних точок - точка торкання прямої l 0 з графіком f. Позначимо абсцис цієї точки через с. Тоді f’(c)=tg α, де α - кут між прямою l 0 та віссю абсцис. Але l||АВ, тому кут α дорівнює куту нахилу січної АВ, тобто. Якщо функція диференційована, то на інтервалі (а; b) знайдеться така точка c∈ (а; b) (рис. 2), що
З рис.1 видно, що кожна з таких «перших» загальних точок - точка торкання прямої l 0 з графіком f. Позначимо абсцис цієї точки через с. Тоді f’(c)=tg α, де α - кут між прямою l 0 та віссю абсцис. Але l||АВ, тому кут α дорівнює куту нахилу січної АВ, тобто. Якщо функція диференційована, то на інтервалі (а; b) знайдеться така точка c∈ (а; b) (рис. 2), що ![]()
- Достатня ознака зменшення функції. Якщо f'(х)< 0 в каждой точке интервала I, то функция f убывает на I.
Достатні ознаки зростання та зменшення функції:
- якщо функція f(x) у кожній точці інтервалу (a, b) має позитивну похідну, то сама функція в цьому інтервалі зростає;
- якщо функція f(x) у кожній точці інтервалу (a,b) має негативну похідну, то функція в цьому інтервалі зменшується.
Визначення. Функція у=f(x) має екстремум (максимум або мінімум) у точці х=х 0 якщо f(x 0) є найбільшим або найменшим значенням функції в деякій околиці цієї точки.
- Екстремуми функції. Дослідження функції екстремуми по 1 похідної.
Функція y=f(x) називається зростаючою (убутною) в деякому інтервалі, якщо при x 1< x 2 выполняется неравенство f(x 1) < f (x 2) (f(x 1) >f(x 2)).
Якщо функція, що диференціюється, y = f(x) на відрізку зростає (зменшується), то її похідна на цьому відрізку f ¢(x) > 0 (f ¢(x)< 0).
Точка x 0 називається точкою локального максимуму (мінімуму) функції f(x), якщо існує околиця точки x 0 для всіх точок якої вірна нерівність f(x) £ f(x 0) (f(x) ³ f(x 0) ).
Точки максимуму і мінімуму називаються точками екстремуму, а значення функції у цих точках – її екстремумами.
Необхідні умови екстремуму. Якщо точка xо є точкою екстремуму функції f(x), або f ¢(x 0) = 0, або f ¢(x 0) немає. Такі точки називають критичними, причому сама функція у критичній точці визначена. Екстремуми функції слід шукати серед її критичних точок.
По 1-ій похідній:
Нехай x 0 – критична точка. Якщо f ¢ (x) під час переходу через точку x 0 змінює знак плюс на мінус, то точці x 0 функція має максимум, інакше - мінімум. Якщо під час переходу через критичну точку похідна не змінює знак, то точці x 0 екстремуму немає.
Необхідні умови екстремуму. Якщо точка x 0 є точкою екстремуму функції f(x), або f ¢(x 0) = 0, або f ¢(x 0) немає. Такі точки називають критичними, причому сама функція у критичній точці визначена. Екстремуми функції слід шукати серед її критичних точок.
- Випуклість графіка функції. Точки перегину.
Випуклість функції, точки перегину
Хорда, що з'єднує точки M 1 (x 1 f (x 1)), M 2 (x 2 f (x 2)) графіка функції f (x) задається функцією
y=L(x, x 1 , x 2) = f(x 1) + f(x 2) (*)
Це перевіряється підстановкою координат x 1 x 2 в праву частину.
Визначення. Функція f(x) називається опуклою вгору на , якщо для x 1 L(x, x 1 , x 2) = f(x 1) Якщо f безперервна на , двічі диференційована (a,b) і f¢¢(x)>0 на (a,b), то f суворо опукла вниз. Доказ. "a£x 1 Визначення. Точка x 0 називається точкою перегину функції f, якщо в точці x 0 існує дотична і в околиці точки x 0 графік f лежить по різні боки від дотичної. Найбільшим значенням функції на відрізку називається найбільше з усіх її значень у цьому відрізку, а найменшим – найменше зі всіх її значень. Розглянемо функцію y=f(x) безперервну на відрізку. Як відомо, така функція досягає свого найбільшого та найменшого значень, або на межі відрізка, або всередині нього. Якщо найбільше чи найменше значення функції досягається у внутрішній точці відрізка, це значення є максимумом чи мінімумом функції, тобто досягається в критичних точках. Таким чином, отримуємо наступне правило знаходження найбільшого та найменшого значень функції на відрізку: 1.Знайти всі критичні точки функції в інтервалі (a, b) та обчислити значення функції у цих точках. 2.Обчислити значення функції на кінцях відрізка за x = a, x = b. 3.З усіх отриманих значень вибрати найбільше та найменше. 1 a.Знайти ОДЗ та точки розриву функції. b.Знайти точки перетину графіка функції з осями координат. 2.Провести дослідження функції за допомогою першої похідної, тобто знайти точки екстремуму функції та інтервали зростання та спадання. 3.Дослідити функцію за допомогою похідної другого порядку, тобто знайти точки перегину графіка функції та інтервали його опуклості та увігнутості. 4.Знайти асимптоти графіка функції: а) вертикальні, b) похилі. 5.На підставі проведеного дослідження побудувати графік функції. Визначення.Функція F(x) називається першорядною для функції f(x) на даному проміжку, якщо для будь-якого х з даного проміжку F"(x)=f(x). Приклад: 1.З'ясувати, чи є функція F(x) = х 3 – 3х + 1 первісною для функції f(x) = 3(х 2 – 1). Рішення: F"(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), тобто F"(x) = f(x) , отже, F(x)є першорядною для функції f(x). Безліч первісних функцій f(x) називається невизначеним інтегралом від цієї функції і позначається символом . Як випливає з викладеного вище, якщо F(x) - деяка первісна функція f(x), то Властивості невизначеного інтеграла, безпосередньо такі з визначення: Приклади плоских фігур Загальне рівняння прямої
Загальне рівняння прямої лінії на площині в декартових координатах: де A, B і C - довільні постійні, причому постійні A і B не дорівнюють нулю одночасно. Вектор з координатами (A,B) називається нормальним вектором і він перпендикулярний до прямої. Вектор з координатами (-B,A) або (B,-A) називається напрямним вектором. Рівняння прямої, що проходить через дві задані точки, що не співпадають
Рівняння прямої, що проходить через дві задані несхожі точки і Параметричні рівняння прямої.
Параметричні рівняння прямої можуть бути записані у вигляді: Канонічне рівняння прямої
Канонічне рівняння виходить із параметричних рівнянь розподілом одного рівняння на інше: Де - координати Х і Y напрямного вектора прямої, та координати точки, що належить прямій. Загальне рівняння
Ax + By + C (> 0).
Вектор = (А; В) – нормальний вектор прямий. Приватні випадки: 1) By + C = 0 – пряма паралельна осі Ox; 2) Ax + C = 0 – пряма паралельна осі Oy; 3) Ax + By = 0 – пряма проходить через початок координат; 4) y = 0 – вісь Ox; 5) x = 0 – вісь Oy. Умова паралельності прямих: k1 = k2. Умова перпендикулярності прямих: k1 · k2 = −1. Кутом між прямими, що перетинаються, на площині, називається градусна міра найменшого з кутів, утворених при перетині цих прямих. Кут між збігаються або паралельними прямими вважається рівним нулю. Кут α між двома прямими, заданими рівняннями: y=k1x+b1 (перша пряма) та y=k2x+b2 (друга пряма), може бути обчислений за формулою (кут відраховується від 1й прямої до 2й проти годинникової стрілки): tg(α)=(k2-k1)/(1+k1k2) Теорема. Якщо пряма, що не лежить у даній площині, паралельна до якої-небудь прямої, що лежить у цій площині, то вона паралельна самій площині. а) пряма лежить у площині; б) пряма та площина мають тільки одну загальну точку; в) пряма та площина не мають жодної загальної точки. Визначення. Дві площини називаються паралельними, якщо вони не мають спільних точок. Паралельність площин і позначається так: | . Розглянемо ознаку паралельності двох площин. Теорема. Якщо дві прямі однієї площини, що перетинаються, відповідно паралельні двом прямим інший площині, то ці площини паралельні. Властивості паралельних площин: Відрізки паралельних прямих, укладені між паралельними площинами, рівні. Ознаки паралельності прямої та площини: 1) Якщо пряма, що лежить поза площиною, паралельна будь-якій прямій, що лежить у цій площині, вона паралельна цій площині. 2) Якщо пряма і площина перпендикулярні до однієї і тієї ж прямої, то вони паралельні. Ознаки паралельності площин: 1) Якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом пересічним прямої іншої площини, то ці площини паралельні. 2) Якщо дві площини перпендикулярні до однієї і тієї ж прямої, то вони паралельні. Ознаки перпендикулярності прямої та площини: 1) Якщо пряма перпендикулярна двом прямим, що перетинаються, лежать у площині, то вона перпендикулярна цій площині. 2) Якщо площина перпендикулярна до однієї з паралельних прямих, то вона перпендикулярна до іншої. Похила до площини. Пряма, що перетинає площину і не перпендикулярна до неї, називається похилою до площини. Теорема про три перпендикуляри. Пряма, що лежить у площині і перпендикулярна до проекції похилої до цієї площини, перпендикулярна і найпохилішій. Ознаки паралельності прямих у просторі: 1) Якщо дві прямі перпендикулярні до однієї і тієї ж площини, то вони паралельні. 2) Якщо в одній із площин, що перетинаються, лежить пряма, паралельна іншій площині, то вона паралельна лінії перетину площин. Ознака перпендикулярності площин: якщо площина проходить через пряму, перпендикулярну до іншої площини, то ці площини перпендикулярні. Теорема про загальний перпендикуляр до двох схрещуються прямим. Для будь-яких двох прямих, що схрещуються, існує єдиний загальний перпендикуляр. ТЕОРЕМА ПРО ТРИ ПЕРПЕНДИКУЛЯРИ. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої. І назад: Якщо пряма на площині перпендикулярна похилій, вона перпендикулярна і проекції похилої. Двогранним кутом називається фігура, утворена двома напівплощинами із загальною прямою, що обмежує їх. Напівплощини називаються гранями, а пряма, що обмежує їх --- рубом двогранного кута. Ознака ПЕРПЕНДИКУЛЯРНОСТІ ПЛОСКОСТЕЙ. Якщо площина проходить через пряму перпендикулярну до іншої площини, то ці площини перпендикулярні. Призма - багатогранник, дві грані якого є конгруентними (рівними) багатокутниками, що у паралельних площинах, інші грані - паралелограмами, мають спільні боку з цими багатокутниками. Види призм: Пряма призма - призма, у якої всі бічні ребра перпендикулярні до основи, інакше призма називається похилою. Площа бічної поверхні прямої призми дорівнює добутку периметра основи на довжину бічного ребра (або висоту). У прямій призмі бічні ребра є висотами. Площа бічної поверхні похилої призми дорівнює добутку перпериметра перпендикулярного перерізу на довжину бічного ребра. Обсяг похилої призми дорівнює добутку площі перпендикулярного перерізу на бічне ребро. Правильна призма - призма в основі якої лежить правильний багатокутник, а бічні ребра перпендикулярні до площин основи. Підстави правильної призми є правильними багатокутниками. Бічні грані правильної призми є рівними прямокутниками. Бічні ребра правильної призми рівні. Правильна призма є прямою. Правильна призма, бічні грані якої є квадратами (висота якої дорівнює стороні основи), є напівправильним багатогранником. Площа бічної поверхні довільної призми, де P – периметр перпендикулярного перерізу, l – довжина бічного ребра. Усіченою пірамідою називається багатогранник, у якого вершинами служать вершини основи та вершини її перерізу площиною, паралельною основі. Обсяг призми: V = S основ H Об'єм прямокутного паралелепіпеда дорівнює добутку площі основи на висоту: V = SH = abc Об'єм піраміди дорівнює одній третині твору площі основи на висоту: де S – площа основи, H – висота піраміди. Об'єм V усіченої піраміди може бути знайдений за формулою де H – висота усіченої піраміди, S1 та S2 – площі її основ. Циліндр (др.-грец. κύλινδρος - валик, ковзанка) - геометричне тіло, обмежене циліндричною поверхнею і двома паралельними площинами, що її перетинають. Циліндрична поверхня - поверхня, що отримується таким поступальним рухом прямої (утворюючої) у просторі, що виділена точка твірної рухається вздовж плоскої кривої (напрямної). Перетин циліндра площиною, паралельної осі, представляє прямокутник. Осьовим перетином називається переріз, який проходить через вісь циліндра. Площа бічної поверхніциліндра дорівнює добутку довжини кола основи на висоту: S=2π rh Повна площа поверхніциліндра: Перетин циліндра. Конус - тіло, отримане об'єднанням всіх променів, що виходять з однієї точки (вершини конуса) та проходять через плоску поверхню. Площа конуса: Усіченим конусом називають тіло обертання, утворене обертанням прямокутної трапеції біля бокової сторони, перпендикулярної до основ. Площа поверхні усіченого конуса: S=π(r12+(r1+ r2) l+ r22) Куля – це тіло обмежене кульовою поверхнею. Сфера (грец. σφαῖρα – куля) – замкнута поверхня, геометричне місце точок у просторі, рівновіддалених від даної точки, званої центром сфери. Площа сфери: Площа сферичної частини поверхні шарового сектора: , де H - висота сегмента. Циліндр (др.-грец. κύλινδρος - валик, ковзанка) - геометричне тіло, обмежене циліндричною поверхнею і двома паралельними площинами, що її перетинають. Конус: Усічений конус: V=1/3π h(r 2 +r 1 ·r 2 +r 2 2) Усічений конус (рис. 1.20) Об'єм кульового сегмента: Об'єм кульового сектора: Властивості: · Паралелепіпед симетричний щодо середини його діагоналі. · Будь-який відрізок з кінцями, що належать поверхні паралелепіпеда і проходить через середину його діагоналі, ділиться нею навпіл; зокрема, всі діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл. · Протилежні грані паралелепіпеда паралельні та рівні. · Квадрат довжини діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірювань. Для знаходження похідної тригонометричної функції
потрібно користуватися таблицею похідних, А саме похідними 6-13. При знаходженні похідних простих тригонометричних функцій
щоб уникнути поширених помилок, слід звертати увагу на наступні моменти: приклад 1.Знайти похідну функції Рішення. Допустимо, з похідної косинусавсе зрозуміло, скажуть багато хто, хто починає вивчати похідні. А як бути з похідної синусадванадцяти, поділених на пі? Відповідь: вважати рівною нулю! Тут синус (функція все-таки!) – пастка, бо аргумент – не змінна ікс або будь-яка інша змінна, а просто число. Тобто, синус цього числа – теж число. А похідна числа (константи), як відомо з таблиці похідних, дорівнює нулю. Отже, залишаємо тільки мінус синус ікса і знаходимо його похідну, не забуваючи про знак: приклад 2.Знайти похідну функції Рішення. Друге доданок - той самий випадок, що і перший доданок у попередньому прикладі. Тобто число, а похідна числа дорівнює нулю. Знаходимо похідну другого доданку як похідну приватного: Приклад 3.Знайти похідну функції Рішення. Це вже інше завдання: тут у першому доданку немає ні арксинусу, ні іншої тригонометичної функції, але є ікс, отже це функція від ікса. Отже, диференціюємо її як доданок у сумі функцій: Тут знадобилися навички у діях з дробами, А саме - у ліквідації триповерховості дробу. Приклад 4.Знайти похідну функції Рішення. Тут літера "фі" відіграє ту ж роль, що "ікс" у попередніх випадках (і в більшості інших, але не у всіх) - незалежної змінної. Тому, коли шукатимемо похідну твори функцій, не поспішатимемо оголошувати рівною нулю похідну кореня від "фі". Отже: Але на цьому рішення не закінчується. Так як у двох дужках зібрані такі члени, від нас ще потрібно перетворити (спростити) вираз. Тому множимо дужки на винесені за них множники, а далі наводимо доданки до спільного знаменника і виконуємо інші елементарні перетворення: Приклад 5.Знайти похідну функції Рішення. У цьому прикладі від нас знання того факту, що існує така тригонометрична функція - секанс - і її формули через косинус. Диференціюємо: Приклад 6.Знайти похідну функції Рішення. У цьому прикладі від нас потрібно пам'ятати зі шкільного курсу формулу подвійного кута. Але спочатку диференціюємо: (це і є формула подвійного кута)![]()

![]()

![]() де C - довільна постійна. Функцію f(x) прийнято називати підінтегральною функцією, твір f(x) dx - підінтегральним виразом.
де C - довільна постійна. Функцію f(x) прийнято називати підінтегральною функцією, твір f(x) dx - підінтегральним виразом.![]()

![]()
 Якщо f(x) безперервна і позитивна на то інтеграл являє собою площу криволінійної трапеції, обмеженої лініями y = 0, x = a, x = b, y = f(x).
Якщо f(x) безперервна і позитивна на то інтеграл являє собою площу криволінійної трапеції, обмеженої лініями y = 0, x = a, x = b, y = f(x).

![]() або у загальному вигляді
або у загальному вигляді де t - похідний параметр, ax, ay - координати x та y напрямного вектора прямої, при цьому
де t - похідний параметр, ax, ay - координати x та y напрямного вектора прямої, при цьому
![]() ;
; ![]()


 Випадки взаємного розташування прямої та площини:
Випадки взаємного розташування прямої та площини:
 Якщо дві паралельні площини перетнуті третьою, то лінії їх перетину паралельні.
Якщо дві паралельні площини перетнуті третьою, то лінії їх перетину паралельні.



 Пірамі́да (ін.-грец. πυραμίς, рід. п. πυραμίδος) - багатогранник, основа якого - багатокутник, а інші грані - трикутники, що мають спільну вершину.
Пірамі́да (ін.-грец. πυραμίς, рід. п. πυραμίδος) - багатогранник, основа якого - багатокутник, а інші грані - трикутники, що мають спільну вершину.![]()

![]()


![]()


![]()
![]()
 Паралелепіпед (від грец. παράλλος - паралельний і грец. επιπεδον - площина) - призма, основою якої служить паралелограм, або (рівносильно) багатогранник, у якого шість граней і кожна з них паралелограм.
Паралелепіпед (від грец. παράλλος - паралельний і грец. επιπεδον - площина) - призма, основою якої служить паралелограм, або (рівносильно) багатогранник, у якого шість граней і кожна з них паралелограм.![]() .
.![]() .
.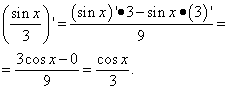
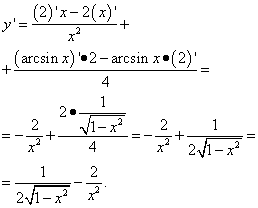
![]() .
.


![]() .
.
![]() ,
,